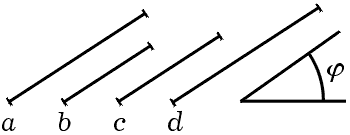
Рис. 16.1. Обломки.
Слова состоят из букв алфавита, предложения из слов, которые можно найти в словаре, и книги из предложений, которые можно найти и у других авторов. Однако если то, что я говорю, содержательно и связано таким образом, что следует одно из другого, то вы столь же можете порицать меня за заимствование моих предложений у других, сколь и за заимствование моих слов у словаря. |
|
| Декарт1 |
1. Предмет настоящей главы. Примеры в первой части этого труда и рассмотрения предыдущих глав второй части, я надеюсь, проливают некоторый свет на роль правдоподобных рассуждений в открытии математических фактов. Но математик не только догадывается; он должен также решать задачи и должен доказывать факты, о которых он догадался. Какова роль правдоподобных рассуждений в открытий решения или в изобретении доказательства? Вот вопрос, который будет рассмотрен в настоящей главе. И вот, между прочим, вопрос, привлёкший внимание автора, который, первоначально интересуясь методами решения задач, в конечном счёте пришёл к теме настоящей книги.
Правдоподобные рассуждения являются темой тонкой и неуловимой, и такой же темой являются методы решения. Пожалуй, было правильно отложить вопрос, объединяющий две такие деликатные темы, до последней главы. Последующее рассмотрение будет кратким; главная цель — указать связь с ранее обсуждавшимися вопросами. Более пространное изложение подошло бы для другой книги о методах решения задач.
2. Рассказ о маленьком открытии. Решение любой простой, но не совсем стандартной математической задачи может потребовать некоторого напряжения и доставить вам триумф открытия. Рассмотрим следующий пример: Построить четырёхугольник, если даны его четыре стороны a, b, c и d и угол φ, образованный противоположными сторонами
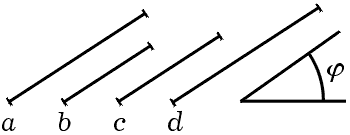
Рис. 16.1. Обломки.
Данные задачи показаны на рис. 16.1: четыре отрезка и один угол, обломки фигуры, разорванной на части, которые мы должны воссоединить, чтобы удовлетворить всем требованиям, предписанным в задаче.
Подразумевается, что стороны a, b, c и d следуют одна за другой вокруг искомого четырёхугольника в этом порядке, так что a противоположна c, а b противоположна d. Угол φ, образованный противоположными сторонами a к c, не является ни одним из четырёх углов четырёхугольника.
Зададим несколько обычных вопросов, которые могут приблизить к нам задачу.
Достаточно ли данных для определения неизвестного? Одних четырёх сторон было бы, очевидно, недостаточно для определения четырёхугольника: четыре палки, соединенные гибкими шарнирами в их соответствующих концах, образуют четырёхугольник, который способен двигаться, деформироваться, не является жестким, не имеет определённой формы. Однако, если один из его четырёх углов фиксирован, шарнирный четырёхугольник не может больше двигаться: четырёхугольник определяется четырьмя своими сторонами и одним из своих углов. Мы можем догадаться, что он определяется также четырьмя сторонами и каким-нибудь другим углом, и, таким образом, данные нашей задачи кажутся достаточными.
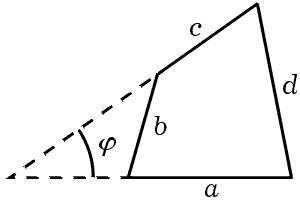
Рис. 16.2. Холодно.
Сделайте рисунок. Мы чертим рис. 16.2, на котором изображены все пять данных, соединённых так, как они должны были бы быть соединены в соответствии с условиями предложенной задачи.
Может случиться, что в этом месте мы застрянем, и в течение известного времени нам в голову не придёт никакой полезной идеи. Действительно, рис. 16.2 выглядит неуклюжим. Стороны a, b, c, d находятся, конечно, на своих правильных местах, но положение
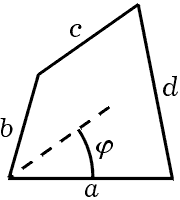
Рис. 16.3. Теплее.
Человек, имеющий опыт в решении задач, попытался бы переделать рисунок, он попытался бы поместить этот угол φ
Но почему же рис. 16.3 кажется многообещающим? Даже хорошие студенты, довольно уверенно это чувствующие, могут не суметь ясно ответить на такой вопрос.
«Он мне кажется хорошим».
«Данные расположены более компактно».
Только студент, исключительно одарённый или опытный, будет в состоянии дать полное объяснение: «На рис. 16.2 угол φ входит в треугольник, однако этот треугольник не годится для построения: у него известны только
Последний ответ указывает, по-видимому, на общую идею: многообещающей кажется любая черта, в отношении которой можно обнаружить, что нынешняя ситуация находится в согласии с удачными ранее встречавшимися ситуациями.
Как бы то ни было, рис. 16.3 оправдывает наши ожидания. В самом деле,
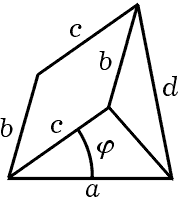 Рис. 16.4. Жарко! |
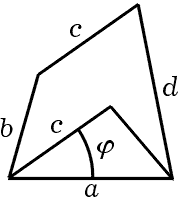 Рис. 16.5. Сделано! |
Для большинства людей, решающих задачи, главным шагом в предыдущем решении, изображённом последовательностью из пяти рисунков, является переход от рис. 16.2 к рис. 16.3; этому шагу может предшествовать длительный период колебаний. Но как только
Предыдущее решение может выявить один или два момента, играющих известную роль и в более важных открытиях.
3. Процесс решения. Решение задачи — крайне сложный процесс. Никакое описание или теория этого процесса не может исчерпать многообразия его сторон, любое его описание или теория обязательно являются неполными, схематичными, чрезвычайно упрощёнными. Я хочу указать место правдоподобных рассуждений в этом сложном процессе и выберу наиболее простое описание, какое я в состоянии найти, в котором это место может быть опознано. И здесь будет достаточно даже начала такого простого описания.
(1) Постановка задачи для себя. Задача становится задачей для вас, когда вы ставите себе целью её решить. Задача ещё не является вашей задачей только потому, что вам на экзамене предложено её решить. Если вы хотите, чтобы
Постановка задачи для себя есть начало решения, существенный первый ход в игре, означающий решимость взяться за задачу.
(2) Избирательное внимание. Вам не нужно мне говорить, что вы поставили себе эту задачу, вам не нужно говорить это себе самому; что вы это сделали, покажет всё ваше поведение. Ваш ум становится избирательным; он становится более доступным для всего того, что выглядит связанным с задачей, и менее доступным для всего, что кажется несвязанным. Вы энергично ухватываетесь за любое воспоминание, замечание, намёк или факт, который мог бы помочь вам решить вашу задачу, и закрываете дверь для всего другого. Когда дверь закрыта так плотно, что вас не достигают даже наиболее настоятельные призывы внешнего мира, люди говорят, что вы поглощены задачей.
(3) Регистрирование темпа продвижения. Есть и другое обстоятельство, показывающее, что вы серьёзно заняты своей задачей; вы становитесь чувствительны. Вы остро чувствуете темп вашего продвижения; у вас поднимается настроение, когда он быстр, вы приходите в уныние, когда он медленен. Обо всём, что бы ни пришло вам на ум, вы быстро составляете мнение: «Это выглядит неплохо», «Это могло бы помочь» или «Плохо», «Не поможет». Такие суждения, конечно, не безошибочны. (Хотя,
(4) Где появляются правдоподобные рассуждения. Несколько более конкретно рассмотрим типичную ситуацию.
Вы пытаетесь добиться решения в известном направлении, на определённом пути. (Например, пытаясь решить геометрическую задачу из § 2, вы отказываетесь от
Однако вам может не повезти. Вы наталкиваетесь на трудности, у вас нет больше продвижения, ничего нового не приходит в голову, и тогда вы начинаете сомневаться: «Было ли это хорошим началом? Правильное ли это направление?» А затем вы можете начать анализировать своё чувство: «Направление казалось вполне правдоподобным — но почему оно правдоподобно?» Затем вы можете приняться обдумывать ситуацию, и вам в голову могут прийти
«Эта ситуация не так уж плоха. Я могу ввести треугольник. В подобных задачах всегда вводят треугольники».
«В конце концов, это было, вероятно, правильное начало. Похоже на то, что это правильное решение. Что мне нужно для решения задачи этого типа? Вот это и это у меня есть. А это? И это есть. А...»
Было бы интересно более отчётливо понять, как люди рассуждают в такой ситуации, в действительности наша главная цель и состоит именно в том, чтобы это понять. Однако, чтобы расширить базу наших наблюдений, нам нужен по крайней мере ещё один пример.
4. Deus ex machina.2 Следующий пример немножко менее прост, чем пример из § 2. Он будет дан в § 6 после некоторых приготовлений в этом параграфе и в следующем.
Математическая книга или лекция прежде всего должна быть правильной и недвусмысленной. Тем не менее мы знаем по тяжёлому опыту, что совершенно недвусмысленное и правильное изложение может быть далёким от удовлетворительного и может казаться невдохновляющим, утомительным или разочаровывающим, даже если излагаемый вопрос сам по себе интересен. Наиболее бросающийся в глаза недостаток в остальном приемлемого изложения есть «deus ex machina». Перед дальнейшими замечаниями я хочу привести конкретный пример. Взглянем на доказательство следующей, не совсем элементарной теоремы.3
Если члены последовательности a1, a2,
| ∞ | ∞ | ||
| ∑ | (a1a2a3...an)1/n < e | ∑ | an. |
| n=1 | n=1 |
Доказательство. Определим числа c1, c2,
для n=1, 2, 3, ... Мы пользуемся этим определением, затем неравенством между средним арифметическим и средним геометрическим и, наконец, тем фактом, что последовательность с общим членом
| ∞ | ∞ | |||
| ∑ | (a1a2a3...an)1/n = | ∑ | (a1c1·a2c2·...·ancn)1/n n + 1 |
≤ |
| n=1 | n=1 | |||
|
(d) | |||||||||||||||||||||||||||
| ∞ | ∞ | ∞ | ∞ | ||||||||||||||
| ≤ | ∑ | akck | ∑ | ( | 1 n |
– | 1 n + 1 |
) | = | ∑ | ak | (k + 1)k kk–1 |
· | 1 k |
< e | ∑ | ak. |
| k=1 | n=k | k=1 | k=1 | ||||||||||||||
5. Эвристическое оправдание. Критический пункт вывода (d) — определение последовательности c1, c2,
«Он кажется кроликом, вытащенным из шляпы».
«Он внезапно появляется из ничего. Он выглядит таким произвольным. Он не имеет никакой видимой мотивировки или цели».
«Я терпеть не могу ходить в темноте. Я терпеть не могу делать шаг, когда не вижу, почему бы он должен был подвести меня ближе к цели».
«Возможно, автор знает цель этого шага, но я её не знаю, и потому не могу следовать за ним с доверием».
«Послушайте, я здесь не для того, чтобы только восхищаться вами. Я хочу научиться, как самому решать задачи. Но я не могу понять, как человек мог напасть на ваше ... определение. Так чему же я могу здесь научиться? Как смог бы я найти такое ... определение сам?»
«Этот шаг не тривиален. Он кажется решающим. Если бы я мог видеть, что он имеет известные шансы на успех, или увидеть для него
Первые ответы не очень ясны, следующие лучше, а последний — самый лучший. Обнаруживается, что разумный читатель или слушатель желает две вещи:
Во-первых; понять, что настоящий шаг рассуждения является правильным.
Во-вторых, понять, что настоящий шаг является подходящим.
Шаг математического рассуждения является подходящим, если он существенно связан с целью рассуждения или если он подводит нас ближе к цели. Недостаточно, однако, чтобы шаг был подходящим: нужно, чтобы, он казался таким читателю. Если шаг простой, совсем тривиальный, обычный шаг, то читатель легко сумеет себе представить, как он мог бы быть связан с целью рассуждения. Если порядок изложения тщательно спланирован, то на мысль о связи этого шага с целью может наталкивать контекст. Если, однако, шаг явно важен, но его связь с целью вообще не видна, то он появляется, как «deus ex machina», и можно понять, что разумный читатель или слушатель разочарован.
В нашем примере определение cn появляется, как «deus ex machina». Но этот шаг является несомненно подходящим. Действительно, рассуждение, основанное на этом определении, доказывает нашу теорему, и доказывает её довольно быстро и ясно. Трудность состоит в том, что рассматриваемый шаг, хотя в конце и оправдывается, не кажется оправданным сначала.
Но как автор мог бы оправдать его с самого начала? Полное оправдание требует некоторого времени; оно даётся полным доказательством. Что нужно — это не полное, а неполное оправдание, правдоподобный предварительный довод, просто намёк, что этот шаг имеет некоторые шансы на успех, короче, некоторое эвристическое оправдание.
6. Рассказ о другом открытии. Почти нет необходимости напоминать читателю, что лучшие рассказы не представляют правды в чистом виде. Они должны, однако, содержать некоторые существенные элементы правды, в противном случае они не были бы даже хорошими. Нижеследующее является несколько «рационализированным» изложением шагов, которые привели меня к доказательству, изложенному в § 4; иными словами, в нём должным образом подчёркивается эвристическое оправдание последовательных шагов.
Теорема, доказанная в § 4, сама по себе удивительна. Мы удивлялись бы меньше, если бы знали, как она была открыта. Мы естественно приходим к ней, пытаясь доказать теорему: Если ряд с положительными членами
сходится, то и ряд
также сходится. Я попытаюсь подчеркнуть некоторые соображения, которые могут нам помочь найти доказательство.
(1) Подходящая известная теорема. Естественно начать с обычных вопросов.
В чём состоит посылка? Мы допускаем, что ряд
В чём состоит заключение? Мы хотим доказать, что сходится ряд
Знаете ли вы теорему, которая могла бы оказаться полезной? Что нам нужно — это какая-нибудь связь между суммой n положительных величин и их средним геометрическим. Встречали ли мы ранее
|
|
Это неравенство показывает, что
|
(a) | |||||||||||||||||||||||||||
— полная неудача! Ряд
(2) Учиться на неудаче. Трудно допустить, чтобы наш план был ошибочным. Хотелось бы верить, что по крайней мере некоторая его часть правильна. Вот полезные вопросы: Что в нашем плане было ошибочно? Какую его часть мы могли бы спасти?
Ряд
(3) Видоизменение подхода. Ошибка состояла в применении неравенства
которые были слишком неравны. Так почему бы не применить его к каким-нибудь родственным величинам, которые имеют больше шансов быть равными? Мы могли бы испытать
Быть может это идея! Мы можем ввести возрастающие компенсирующие множители, например 1, 2,
Можно было бы λ оставить на время неопределённым и выбрать наиболее выгодное значение позже. Этот план имеет столько хороших черт, что кажется созревшим для исполнения:
|
(b) | ||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||
Мы натолкнулись на трудное место. Оценить последнюю сумму мы не можем. Даже если мы вспомним различные приёмы, имеющие отношение к данному случаю, то всё же будем вынуждены работать с «сырыми равенствами»
| (n!)1/n ≈ | n e |
, |
| ∞ | ∞ | ∞ | ||||||||
| ∑ | 1 n (n!)λ/n |
≈ eλ | ∑ | 1 n1+λ |
≈ eλ | ∫ | dx x1+λ |
= | eλ λkλ |
. |
| n=k | n=k | k | ||||||||
Вводя это в последнюю сумму формулы (b), мы очень близко подходим к доказательству того, что
|
(b') |
где C — некоторая постоянная, возможно
(4) Вновь просматривая предыдущее рассуждение, мы вынуждены повторить вопрос: «Какое значение λ наиболее выгодно?» Вероятно, то λ, которое делает
Это определённо наводит на мысль, что наиболее очевидный выбор и наиболее выгоден: в качестве компенсирующего множителя при an нужно взять
(5) Больше гибкости. В нашем предыдущем рассуждении (b) мы оставили λ неопределённым. Это придало нашему плану известную гибкость: значение λ оставалось в нашем распоряжении. Почему бы не придать нашему плану ещё большую гибкость? Мы могли бы оставить компенсирующий множитель при an совсем неопределённым; обозначим его буквой cn и распорядимся его значением позднее, когда яснее увидим, что нам нужно. Перейдём к этой дальнейшей модификации нашего первоначального подхода:
|
(c) | ||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||
Как нам следовало бы выбрать cn? Это — решающий вопрос, и мы больше не можем откладывать ответ.
Во-первых, мы легко видим, что множитель пропорциональности должен оставаться произвольным. Действительно, последовательность cc1,
Во-вторых, наша предшествующая работа наводит на мысль, что и cn и
| cn ~ Kn, (c1c2...cn)1/n ~ | Kn e |
= K'n. |
В-третьих, больше всего желательно, чтобы мы были в состоянии найти сумму ряда
| ∞ | ||
| ∑ | 1 n (c1c2 ... cn)1/n |
. |
| n=k | ||
В этом месте нам понадобятся все наши знания о простых рядах. Если мы знакомы с рядом
| ∑ | 1 n(n + 1) |
= | ∑ | ( | 1 n |
– | 1 n + 1 |
) | , |
то велика вероятность, что в этой связи мы о нём вспомним. Этот ряд обладает тем свойством, что его сумма имеет простое выражение не только от
Теперь, очевидно,
Поскольку
| cn = | (n + 1)n nn–1 |
= | ( | 1 + | 1 n |
) | n | n ~ en; |
асимптотическая пропорциональность n является хорошим признаком! И возникает число e — очень хороший признак!
Мы выбираем эти cn, и после этого выбора снова возвращаемся к
Теперь мы можем понять, как человек мог открыть то определение cn, которое появилось в § 4 как «deus ex machina».
7. Несколько типичных указаний. Мы рассмотрели в предыдущих параграфах два примера. Сначала мы исследовали «задачу на нахождение»
Перечисляя такие оценивающие указания, мы не будем пытаться добиться полноты. В некоторых случаях мы будем находить необходимым делать различие между задачами на нахождение и задачами на доказательство. В таких случаях мы будем давать две параллельные формулировки и первой давать формулировку, относящуюся к задачам на нахождение.
Рассмотрим ситуацию, в которой человек, решающий задачу, естественно сталкивается с правдоподобным рассуждением. Вы заняты интересной задачей. Вы задумали план решения, но
A. Этот план решения можно осуществить.
Когда вы исследуете ваш план под различными углами зрения, вам может прийти на ум несколько за и против. Вот некоторые бросающиеся в глаза типичные указания, которые могут говорить в пользу
B1. Этот план принимает в расчёт все данные.
Эта формулировка относится к задачам на нахождение. Имеется параллельная формулировка, относящаяся к задачам на доказательство: этот план принимает в расчёт все части посылки. Например,
B2. Этот план обеспечивает связь между данными и неизвестным.
Имеется параллельная формулировка, относящаяся к задачам на доказательство: этот план обеспечивает связь между посылкой и заключением. Например, в
B3. Этот план имеет черты, часто оказывающиеся полезными при решении задач такого типа.
Например, план, начинающийся с
B4. Этот план похож на план, с помощью которого удалось решить аналогичную задачу.
B5. С помощью этого плана удалось решить задачи в частном случае.
Например, у вас есть план для решения трудной задачи, относящейся к произвольной замкнутой кривой. Прямое проведение этого плана,
B6. С помощью этого плана удалось решить часть задачи (найти некоторые из неизвестных или доказать более слабое заключение).
Этот перечень ни в коем случае не является исчерпывающим. Существуют и другие типичные указания и признаки, но нам нет необходимости их здесь перечислять. Во всяком случае, было бы бесполезно перечислять их без должной иллюстрации.
8. Индукция в изобретении. Предположение A человека, решающего задачу (что его план решения можно осуществить), может быть подкреплено одним, двумя или большим числом указаний B1, B2,
(1) Когда человек, решающий задачу, обдумывает свой план решения, этот план обычно является скорее «текучим», чем «жёстким», он больше чувствуется, чем формулируется. В самом деле, для этого человека было бы глупо преждевременно фиксировать свой план. Умный человек не связывает себя жёстким планом. Даже на более позднем этапе, когда план более созреет, он сохраняет этот план пригодным для видоизменений, оставляет ему некоторую гибкость, принимает во внимание непредвиденные трудности, к которым он может оказаться вынужденным приспосабливать свой план. Поэтому, когда он исследует осуществимость своего плана, он рассматривает изменчивый, иногда очень недолговечный объект.
С другой стороны, предположения, которые исследует математик или натуралист, обычно являются довольно определёнными: они ясно сформулированы или по крайней мере разумно близки к ясной формулировке. И присяжные должны исследовать довольно определённое предположение: обвинительный акт, выражения которого тщательно подобраны обвинением.
Отметим это существенное различие между исследованием человеком, решающим задачу, осуществимости его плана и индуктивным исследованием математического или физического предположения или судебным исследованием обвинения: это различие между изменчивым, или очень недолговечным, и неизменным, сравнительно хорошо определённым объектом.
(2) Заседания и решения суда присяжных заносятся в протокол. Предположение, исследуемое натуралистом, и доводы, собранные за или против него, также предназначены для постоянного протоколирования. Не так обстоит дело с предположением человека, решающего задачу, относительно осуществимости его схемы или с признаками, говорящими за или против неё: их значение мимолётно. Они крайне важны в то время, когда они руководят действиями человека, решающего задачу. Но когда его работа вступает в новую фазу, сам план может измениться, и тогда указания, говорящие за или против этого плана, теряют почти всякий интерес. В конце, когда решение достигнуто и задача решена, все такие аксессуары отбрасываются. Окончательная форма решения может быть записана, но изменявшиеся планы и аргументы за или против них в большей части или целиком забываются. Воздвигнутое здание остаётся на виду, но леса, которые были необходимы, чтобы его воздвигнуть, удаляются.
Отметим этот аспект различия между индуктивным или судебным исследованием, с одной стороны, и оценкой человеком, решающим задачу, перспектив своего плана — с другой: первое постоянно протоколируется, а второе нет.
(3) Предположение A и указания B1, B2,
A. Этот план решения можно осуществить в его теперешней форме.
В. Этот план решения принимает в расчёт все данные.
Чтобы описать эту ситуацию точнее, прибавим: Известно, что каждое из данных необходимо. Если это так, то
Действительно, если бы план мог быть осуществлён и дать правильное решение, он должен был бы использовать все данные, каждое из которых необходимо для решения.
Теперь важно ясно себе представить ситуацию: A — предположение, в котором человек, решающий задачу, естественно заинтересован, B — утверждение, которое может быть истинным или нет. Исследуем обе возможности.
(4) Если для решения необходимы все данные, но наш план решения не принимает всех данных в расчёт, то наш план в его теперешней форме не может быть осуществлён. (Он мог бы быть осуществлён в видоизмененной форме.) Иными словами, если Bложно, то и A должно быть ложно.
Теперь важно отметить, что мы могли бы прийти к этому заключению и с помощью формального рассуждения. Действительно, мы следовали здесь классической элементарной схеме рассуждения «modus tollens», так называемого гипотетического силлогизма:
| Из A следует B В ложно |
| A ложно |
(5) Если, однако, наш план решения действительно принимает в расчёт все данные, то естественно рассматривать это обстоятельство как благоприятный признак, как хорошую примету, что наш план может быть осуществлён. (Я представляю себе вид человека, решающего задачу, когда он замечает, что данное, которое, как ему казалось сначала, его план не учитывает, в конце концов оказалось использованным планом, и при этом хорошо использованным.) Короче говоря, если B истинно, то A становится более правдоподобным. Теперь важно отметить, что в действительности мы могли бы прийти к этому заключению, просто следуя нашей фундаментальной индуктивной схеме:
| Из A следует B В истинно |
| A более правдоподобно |
(6) Рассмотрим теперь другую ситуацию. Она сходна с ситуацией, объяснённой в (3) и разобранной в (4) и (5), но явным образом от неё отлична. Снова мы интересуемся предположением A человека, решающего задачу, и указанием B, подкрепляющим это предположение. Однако ситуация теперь иная (менее чётко определённая). A и B имеют значения:
A. Этот план решения может быть осуществлён (быть может, в видоизменённой форме).
B. Этот план решения принимает в расчёт все данные.
Чтобы охарактеризовать эту ситуацию более полно, прибавим: Мы сильно подозреваем, хотя и не знаем определённо, что все данные необходимы.
Как и выше, A — предположение, в котором человек, решающий задачу, очень заинтересован, а B — утверждение, которое может быть истинным или нет. Мы должны исследовать обе возможности.
Если B оказывается ложным, то появляется довод против A, но он не является полностью решающим. Поскольку B ложно, наш план не принимает в расчёт всех данных; тем не менее мы можем придерживаться нашего плана (если мы имеем для него
Если B оказывается истинным, то мы можем принять это обстоятельство за ободряющий признак. Действительно, даже если из A не следует B, и, таким образом, B вместе с A не является несомненным, всё же может быть, что
| B вместе с A весьма правдоподобно, B без A не в такой мере правдоподобно. |
В таком случае подтверждение можно рассматривать как своего рода косвенную улику в
(7) В предыдущих пунктах (3), (4), (5) и (6) мы рассмотрели указание, обозначенное в § 7 символом B1 (мы обозначали его просто B). Рассмотрение других указаний, перечисленных в § 7 (указаний B2,
Как мы уже видели, из A может следовать B1, но даже если это и не так и B1 не обязательно присоединяется к A, могут иметься сильные шансы в пользу того, что A будет сопровождаться B1. Такой же характер имеет отношение A к B2 (или B3, или
Следовательно, если мы сомневаемся в предположении A, но нам удалось наблюдать B1, или B2, или
(8) Если, несмотря на значительный труд, натуралисту удаётся подтвердить только несколько, не слишком уж неожиданных следствий своего предположения, то он может быть вынужден от него отказаться. Если против подсудимого предъявлено слишком мало улик, суд может прекратить дело. Если после долгих и напряжённых усилий человеку, решающему задачу, пришло на ум только несколько слабых указаний в пользу его плана, то он может быть вынужден радикально изменить свой план или даже совсем его отбросить.
С другой стороны, если было подтверждено несколько следствий, было предъявлено несколько улик против подсудимого, было подмечено несколько указаний, то доводы в пользу предположения натуралиста, в пользу обвинения или в пользу плана человека, решающего задачу, могут значительно усилиться. Однако даже более важную роль, чем число, может играть разнообразие. Следствия, очень отличающиеся одно от другого, свидетели, являющиеся очевидно независимыми, указания, приходящие с различных сторон, следует рассматривать как более веские.
(9) Несмотря на такое сходство, существует и заметное различие. Цель натуралиста — собрать за или против своего предположения столько доводов, сколько ему удастся. Цель суда — исследовать все относящиеся к делу предъявленные улики. Однако цель человека, решающего задачу, отнюдь не состоит в том, чтобы собрать столько, сколько ему удастся, доводов за или против своего плана решения или до самого конца обдумать эти доводы: его цель —решить задачу любыми средствами, следуя своему плану решения, или
Даже ошибочный план может служить цели человека, решающего задачу. Чтобы решить свою задачу, он должен мобилизовать и организовать относящиеся к рассматриваемому вопросу части своего прошлого опыта. Работая с ошибочным планом, но с настоящим напряжением, он может расшевелить
(10) Два человека, которым представлены одни и те же доводы, могут честно быть несогласны, даже если они руководствуются одними и теми же схемами правдоподобных рассуждений. Их фоны могут быть различными. Мои несформулированные, неясные основания, весь мой фон может оказывать влияние на мою оценку экспериментальных данных или судебных улик. Ещё большее влияние могут они оказывать на мою оценку указаний за или против моего плана решения, и это не неразумно. Разумно, что, работая над решением задачи, больше веса, чем при других условиях, я должен придавать внушениям моего фона, и меньше веса — отчётливо сформулированным основаниям: расшевелить подходящий материал, скрытый
Тем не менее мне кажется, что одно из главных достоинств человека, закалённого в решении задач, состоит в том, что он может проницательно оценивать указания за или против осуществимости своего плана, как прошедший хорошую школу натуралист оценивает экспериментальные данные или опытный юрист — судебные улики.
9. Несколько слов преподавателю. Математику можно рассматривать с различных точек зрения. Многим учащимся, я опасаюсь, математика кажется собранием жёстких правил, часть из которых перед заключительными экзаменами следует выучить наизусть, и все их после этого можно позабыть. Некоторым преподавателям математика кажется системой строгих доказательств, от изложения которых в классе следует, однако, воздержаться, а вместо них изложить какой-нибудь более доступный, хотя и не имеющий силы доказательства рассказ, которого вы немножко стыдитесь. Математику, являющемуся активным исследователем, математика иногда может казаться игрой в догадки: вы должны догадаться о математической теореме, перед тем как её докажете, вы должны догадаться об идее доказательства, перед тем как проведёте его в деталях.
Философу с довольно широкими взглядами, я думаю, все разумные приобретения знаний должны иногда казаться игрой в догадки. В науке, как и в повседневной жизни, встретившись с новой ситуацией, мы начинаем с какой-нибудь догадки. Наша первая догадка может бить мимо цели, но мы испытываем её и в соответствии со степенью успеха более или менее её видоизменяем. В конечном счёте после нескольких испытаний и нескольких видоизменений, толкаемые наблюдениями и ведомые аналогией, мы можем прийти к более удовлетворительной догадке. Неспециалист не находит удивительным, что натуралист работает таким образом. Знания натуралиста могут быть лучше упорядочены с целью отбора подходящих аналогий, его наблюдения могут быть более целеустремленны и более тщательны, он может давать своим догадкам более причудливые названия и называть их «ориентировочными обобщениями», но натуралист подобно обычному человеку приспосабливает свой ум к новой ситуации с помощью догадок. И неспециалист не удивляется, когда слышит, что натуралист подобно ему самому догадывается. Неспециалисту может казаться несколько более удивительным, что и математик также догадывается. Результат творческой работы математика — доказательное рассуждение, доказательство, но доказательство открывают с помощью правдоподобных рассуждений, с помощью догадки.
Если это так, а я верю, что это так, то для догадки должно быть место и в преподавании математики. Обучение должно подготавливать к изобретению, или по крайней мере давать некоторое представление об изобретении. Во всяком случае, обучение не должно подавлять в учащемся ростки изобретательности. Учащийся, немного интересующийся рассматриваемой в классе задачей, ожидает решение определённого типа. Если учащийся смышлён, то он в
Я не говорю, что мы должны пренебрегать доказательствами. Наоборот, нам следует учить и доказывать и догадываться, учить обоим видам рассуждений: доказательному и правдоподобному. Для учащегося ценнее, чем любому частному математическому факту или приёму, теореме или аппарату, научиться двум следующим вещам:
Во-первых, отличать строгое доказательство от нестрогой попытки, доказательство от догадки.
Во-вторых, отличать более разумную догадку от менее разумной догадки.
Существуют частные случаи, когда важнее учить догадываться, чем доказывать. Возьмите преподавание дифференциального и интегрального исчисления студентам технических учебных заведений. (Я имею длительный и разнообразный опыт такого преподавания.) Инженерам нужна математика, совсем немногие из них имеют здоровый интерес к математике, но они не приучаются понимать
Я сказал, что желательно учить догадываться, но не сказал, что этому учить легко. Нет никакого абсолютно верного метода для догадок, и потому не может быть никакого абсолютно верного метода для обучения тому, как догадываться. Я мог, пожалуй, в предыдущем сказать несколько глупостей, но, надеюсь, я избежал наибольшей глупости — претензии на то, что у меня есть безошибочный метод, позволяющий учить догадываться.
Тем не менее учить догадываться не невозможно. Я надеюсь, что в этом отношении могут оказаться полезными некоторые из подробно объяснённых примеров и некоторые из предложенных в этой книге упражнений. Они имеют наилучшие шансы попасть на плодородную почву у преподавателей, имеющих длительный опыт в решении задач.
Возьмите, скажем, пример, рассмотренный в §§ 4 и 6. Два изложения в §§ 4 и 6 очень различны. Наиболее бросающееся в глаза различие состоит в том, что одно из них короткое, а другое длинное. Наиболее существенное различие состоит в том, что одно даёт доказательства, а другое — правдоподобности. Одно предназначено для того, чтобы проверить доказательные заключения, оправдывающие последовательные шаги. Другое приспособлено для того, чтобы дать известную возможность заглянуть в эвристические мотивы некоторых шагов. Доказательное изложение следует принятому способу, обычному со времен Евклида; эвристическое изложение крайне необычно в печати. Однако наблюдательный преподаватель может пользоваться обоими способами изложения. Действительно, он мог бы придумать, если нужно, третье изложение, находящееся между этими двумя, с должным учётом имеющегося в распоряжении времени интереса своих учеников, всех условий, в которых он работает.4
Эта книга главным образом адресуется учащимся, желающим развить свои способности, и читателям, желающим узнать о правдоподобных рассуждениях и их не столь уж банальных связях с математикой. Не игнорировались, я надеюсь, и интересы преподавателя, но они удовлетворялись скорее косвенно, чем прямо. Я надеюсь
1. Преподавателю: некоторые типы задач. Эта книга предназначена служить различным категориям читателей: тем, кто желает понять, как догадываются, тем, кто желает научиться догадываться, и тем, кто желает учить догадываться. Читатель последней категории редко является непосредственным адресатом, но наблюдательный преподаватель мог бы
Догадаться и доказать. О математических фактах сначала догадываются, а затем их доказывают, и почти каждое место в этой книге старается показать, что это — нормальный образ действий. Если изучение математики должно иметь
Испытать следствия. Философы и нефилософы расходятся в мнениях относительно почти всего, касающегося индукции, но существует мало сомнений в том, что наиболее обычный индуктивный приём состоит в исследовании общего утверждения путём испытания его частных следствий. Этот индуктивный приём ежедневно применяется в математическом исследовании и мог бы ежедневно применяться в классе с реальной пользой для учащихся. См. пример 12.2 и примеры
Вы можете сделать ошибочную догадку. Вам следовало бы приобрести некоторый опыт в догадках. Вам следовало бы из личного соприкосновения с реальными вещами знать, что догадки могут быть серьёзными, что догадки могут вести к ошибке и что даже ваши собственные вполне серьёзные догадки могут вести к ошибке. Для такого опыта решите примеры
Теория в малом масштабе. Почти на каждой странице этой книги
2. Четырёхугольник разрезается своими двумя диагоналями на четыре треугольника. Назовём два из этих треугольников «противоположными», если они имеют общую вершину, но не имеют общей стороны. Докажите утверждения:
(a) Произведение площадей двух противоположных треугольников равно произведению площадей двух других противоположных треугольников.
(b) Четырёхугольник является трапецией в том и только в том случае, если существуют два равновеликих противоположных треугольника.
(c) Четырёхугольник является параллелограммом в том и только в том случае, если все четыре треугольника равновелики.
Решение
3. (a) Докажите следующую теорему: Точка лежит внутри равностороннего треугольника и имеет соответственно расстояния x, y и z от трёх его сторон;
(b) Точно сформулируйте и докажите аналогичную теорему пространственной геометрии относительно расстояний внутренней точки от четырёх граней правильного тетраэдра.
(c) Обобщите обе теоремы так, чтобы они относились к любой точке соответственно на плоскости или в пространстве (а не только к точкам внутри треугольника или тетраэдра). Дайте точные формулировки и доказательства.
Решение
4. Рассмотрите предложения (I)–(IV), которые не обязательно верны:
(I) Если многоугольник, вписанный в окружность, является равносторонним, то он также и равноугольный.
(II) Если многоугольник, вписанный в окружность, является равноугольным, то он также и равносторонний.
(III) Если многоугольник, описанный вокруг окружности, является равносторонним, то он также и равноугольный.
(IV) Если многоугольник, описанный вокруг окружности, является равноугольным, то он также и равносторонний.
(a) Установите, какие из этих четырёх предложений верны и какие неверны, давая в каждом случае доказательство вашего утверждения.
(b) Если вместо произвольных многоугольников мы рассматривали бы только четырёхугольники, то какие из этих четырёх предложений были бы верны и какие неверны?
(c) Как обстоит дело с пятиугольниками?
(d) Можете вы догадаться о каких-нибудь более широких утверждениях или, быть может, даже доказать их? Они должны объяснить ваши наблюдения (b)
Решение
5. Пусть α, β и γ — углы треугольника. Покажите, что
(a)
(b)
(c)
Решение
6. Рассмотрите усечённую правильную пирамиду с квадратными основаниями. Назовите «средним сечением» сечение усечённой пирамиды плоскостью, параллельной основаниям и находящейся от них на одинаковом расстоянии. Назовите «промежуточным прямоугольником» прямоугольник, одна сторона которого равна стороне нижнего, а другая — стороне верхнего основания.
Четыре различных ваших друга согласны, что объём этой усечённой пирамиды равен произведению высоты на некоторую площадь, но они расходятся в мнениях относительно этой площади и делают четыре различных предположения:
(I) Площадь среднего сечения.
(II) Среднее арифметическое площадей нижнего и верхнего оснований.
(III) Среднее арифметическое площадей нижнего и верхнего оснований и среднего сечения.
(IV) Среднее арифметическое площадей нижнего и верхнего оснований и промежуточного прямоугольника.
Пусть h — высота усечённой пирамиды, a — сторона её нижнего основания и
Решение
7. Qui nimium probat, nihil probat. Иными словами, если вы доказываете слишком много, то вы ничего не доказываете. Я не могу сказать, в каком смысле изобретатель этой классической поговорки намеревался ею пользоваться, но хочу объяснить то значение этого изречения, которое с тех пор, как я приступил к математической работе, я нахожу чрезвычайно полезным. Это изречение напоминает мне об одном из наиболее полезных признаков, с помощью которых мы можем судить об осуществимости плана решения.
Вот ситуация: вы хотите доказать какое-то предложение. Это предложение состоит из заключения и посылки, которая имеет несколько пунктов, и вы знаете, что каждый из этих пунктов необходим для заключения, т.е. что ни один из них не может быть отброшен без того, чтобы заключение вашего предложения не стало несправедливым. Вы задумали план доказательства и взвешиваете шансы вашего плана. Если ваш план не вовлекает в игру все эти пункты, то вам следует видоизменить ваш план или же отвергнуть его: если бы он был осуществим, как он есть, и привёл бы к доказательству заключения, хотя он и не учитывает тот или иной пункт посылки, то он доказал бы слишком много, т.е. нечто ложное, и таким образом он не доказал бы ничего.
Я сказал, что ваш план должен вовлекать в игру эти пункты. Я имею в виду, что одних лишь словоизлияний не достаточно, простое их упоминание в счёт не идёт: ваш план должен обеспечивать существенное использование каждого пункта посылки в доказательстве. Каркас, который должен поддерживать заключение, не может быть воздвигнут, если он не имеет крепкой опоры в каждом пункте посылки.
Может оказаться очень трудным придумать план, должным образом вовлекающий в игру все пункты посылки. Поэтому, если план обещает уловить все эти пункты, то мы приветствуем его с облегчением: это превосходный признак, сильное указание на то, что план можно осуществить.
По поводу соответствующих «задач на нахождение», все данные которых необходимы,
Если вы предпочитаете латинской поговорке французское изречение, то вот оно: «La mariée est trop belle» — новобрачная слишком красива. Я не думаю, что мне нужно распространяться на эту тему; после предыдущего читатель может сам представить себе все подробности.
8. Близость и правдоподобность. Насколько далеко решение? Сколько остаётся доделать? Такие вопросы тяжёлым грузом лежат на сознании учащегося, который должен окончить свою задачу за назначенное время, но они присутствуют в сознании каждого человека, решающего задачу.
(1) Мы даже в состоянии до некоторой степени ответить на такие вопросы, конечно, не точно, но я склонен верить, что в среднем довольно правильно.
Например, посмотрим снова на рис. 16.1–16.5 и на процесс решения, который они изображают. Человек, решающий задачу, может чувствовать, что рис. 16.3 значительно ближе к решению, чем рис. 16.2; и как только он придёт к рис. 16.4, он может чувствовать, что решение в пределах лёгкой достижимости.
Оценивая близость решения, мы можем полагаться на неясные чувства или на более отчётливые признаки. Любой признак, указывающий, что наш план решения осуществим, может быть истолкован также и как признак продвижения к решению и может помочь нам оценить расстояние, которое нам ещё осталось пройти.
(2) Рассмотрим решение «задачи на доказательство». Цель состоит в доказательстве (или опровержении) некоторой теоремы. Человек, решающий задачу, может верить или не верить в теорему, которую он доказывает. Однако, если он сколько-нибудь хорошо умеет решать задачи, то он должен быть готов к пересмотру своих мнений. И, таким образом, вопросы «Правдоподобна ли теорема? Насколько она правдоподобна?» всегда присутствуют в его сознании, хотя иногда более, а иногда менее на переднем плане. Если в его поле зрения попадает
(3) Припоминание когда-то известной, но теперь забытой фамилии является задачей более простой, чем математическая задача, но несколько с ней сходной. Мы часто можем наблюдать людей, пытающихся припомнить фамилию, и на таких наблюдениях мы могли бы научиться нескольким интересным вещам.
В разговоре ваш друг хочет назвать вам какую-то фамилию (хозяина магазина, или фамилию знакомого, или, может быть, автора). Он запинается, и вы слышите его слова: «Сейчас я её назову», или «Подождите немножко, я через некоторое время её вспомню», или «Как это ни глупо, но я не могу теперь вспомнить, хотя уверен, что эта фамилия придёт мне в голову через несколько часов, возможно, завтра утром». Очевидно, ваш друг пытается оценить близость этой фамилии, пытается измерить своего рода «психологическое расстояние». Я высказал бы догадку, что его предсказание окажется приблизительно верным, что его оценка этого «психологического расстояния» в общих чертах правильна.
С точки зрения возможного сравнения с решением задачи интересно также отметить, что человек, который не в состоянии вспомнить фамилию полностью, может быть в состоянии вспомнить её частично или, пожалуй, лучше сказать, он может быть в состоянии вспомнить некоторые черты этой фамилии. Вы можете слышать, как ваш друг говорит: «Фамилия не Баттенберг — он, в конце концов, не муж королевы,5 — но это немецкая фамилия из трёх слогов, очень похожая на Баттенберг». И (я наблюдал такие случаи) ваш друг, может быть, совершенно прав во всех этих подробностях, хотя правильная фамилия придёт ему на ум только через несколько дней.
Совсем таким же образом математик, хотя он ещё и не решил свою задачу, может предвидеть некоторые черты её решения вполне надёжно.
Те аспекты решения задач, которые наиболее интересны для будущего математика или для преподавателя, не легко поддаются обычным методам экспериментальной психологии. Возможно, припоминание фамилии, процесс в
9. Вычисления и правдоподобные рассуждения. Хотя числа часто рассматриваются как символы наиболее высокой достижимой достоверности, результаты вычислений никоим образом не являются достоверными; они только правдоподобны. Вычисления во многих отношениях зависят от правдоподобных рассуждений.
(1) Вы должны проделать длинное вычисление. Окончательный результат достигается последовательностью шагов. У вас очень хорошие шансы сделать правильно любой отдельный шаг, но шагов много, в каждом шаге есть возможность ошибиться, и окончательный результат может быть неверным. Как предохранить себя от ошибки?
Вычислите искомое число дважды с помощью как можно более отличающихся способов. Если эти два вычисления дадут различные результаты, то, несомненно, по крайней мере один из них неверен, но, возможно, что и оба неверны. Если два вычисления находятся в согласии, то никоим образом не несомненно, что дважды полученный результат правилен, но он может оказаться правильным, а согласие является указанием его правильности. Вес этого указания зависит от различия между двумя способами, которыми мы воспользовались.
Например, этот вес очень мал, если, проделав вычисление один раз, вы немедленно после этого повторите его без какого бы то ни было изменения в методе: с первым вычислением, ещё свежим в вашем уме и в ваших пальцах, вы легко можете оступиться на том же месте, где оступились в первый раз. Повторить вычисление после того, как пройдёт известное время, немножко лучше, дать проделать его во второй раз другому человеку значительно лучше, проделать второе вычисление совсем другим методом ещё лучше.
Действительно, если два совершенно различных способа приводят к одинаковому результату, то мы имеем только два очевидных предположения: результат может быть правильным или согласие может быть вызвано случайностью. Если вероятность согласия
Чем больше отличаются способы двух вычислений, тем более реалистична простейшая оценка вероятности их согласия: вероятность того, что два вычисления
При вычислениях большого масштаба является хорошим обычаем делать случайность совпадения ещё более невероятной посредством введения многократного контроля. Два вычисления выполняются методами, настолько различными, насколько возможно по обстоятельствам, однако так, чтобы, если они правильны, совпадали не только их окончательные результаты, но и несколько промежуточных результатов. Когда степень согласия возрастает, становится всё более и более трудно приписать его простой случайности, хотя, конечно, случайность никогда не может быть полностью исключена и результат никогда не может быть полностью гарантирован.
(2) До сих пор мы молчаливо допускали как известное, что два вычисления, результаты которых мы сравниваем, теоретически строго эквивалентны. Однако в прикладной математике мы часто должны работать с приближениями и можем сравнивать числовые результаты, которые не обязаны полностью совпадать, даже если все совершаемые арифметические операции безошибочны; мы только надеемся, что они будут «грубо» совпадать. Кроме того, теория метода приближения, с которым мы работаем, может быть очень плохо известна. При таких обстоятельствах, конечно, сфера приложения правдоподобных рассуждений является даже более широкой и такие рассуждения более рискованны. Ср. пример 11.23.
(3) Два математика, A к B, исследовали одно и то же множество из девяти комбинаторных задач. Нам нет необходимости знать содержание этих задач (они относятся к гиперкубу в четырёхмерном пространстве), но важно знать, что они расположены в порядке возрастающей трудности. Первые две задачи тривиальны, третья лёгкая, четвёртая труднее, затем они становятся всё более и более сложными, а последняя задача является наиболее трудной.
И A, и B решили задачи, но их результаты не вполне согласны. Вот их решения этих девяти задач:
Иными словами, A и B согласны в отношении первых шести задач, более лёгких, но несогласны в отношении трёх последних задач, более трудных. На самом деле, они следовали различным методам.
A решал каждую из этих девяти задач независимо от других. Его метод для каждой задачи несколько иной, и по мере того, как он переходит к более трудным задачам, его метод становится всё более сложным.
B решал задачи с помощью единого метода. Его работа состояла из двух частей. Первая часть, более трудная, была подготовительной для решения всех девяти задач. Вторая часть, более стандартная, применяла результат первой части к каждой отдельной задаче в соответствии с единообразным правилом. При решении задач методом математика B они кажутся значительно менее отличающимися по трудности, чем при их решении методом
Мне кажется, что описанная ситуация даёт нам разумное основание больше верить решению B, чем
Поскольку эти два очень различных метода приводят к одинаковым результатам в первых шести задачах и эти задачи
Так как результат первой части работы математика B в 3 случаях из 9 подтверждается своими следствиями и,
Если, однако, первая часть работы B была правильна (как это,
Только что рассмотренный случай является довольно специальным, но он показывает, что существуют дальнейшие возможности в исследовании схем правдоподобных рассуждений. Например, благодарной может оказаться задача выразить, как можно лучше, только что изложенное правдоподобное рассуждение в формулах исчисления вероятностей.
10. Вы должны сложить столбец из десяти шестизначных чисел, начинающийся, например, так:
Опишите различные способы, которыми можно это сделать.
Способы
11. Назовите «элементарным шагом» прибавление написанного однозначного числа к двузначному числу, которое вы держите в уме; включите, однако, возможность (делающую шаг более лёгким), что второе число также написано или что оно имеет только один знак. Сколько потребуется элементарных шагов, чтобы выполнить упомянутое в примере 10 сложение наиболее обычным способом?
Ответ
12. Производя вычисление, вы получаете сначала два девятизначных числа, а затем окончательный результат как их разность, которая оказывается трёхзначным числом. При другом способе вычисления то же самое трёхзначное число вы получаете в результате как разность двух семизначных чисел. Пользуясь формулой, приведённой в
Ответ
13. Формальное доказательство и правдоподобные рассуждения. Вы должны проделать длинное вычисление. Окончательный результат достигается последовательностью шагов и должен быть правильным, если правилен каждый шаг. Каждый отдельный шаг (например, сложение
Вы проводите длинное математическое доказательство. Предполагается, что это доказательство разлагается на шаги, каждый из которых вы полностью можете проверить, и окончательное заключение должно быть правильным, если правилен каждый шаг. Однако подобно всякому другому, вы можете делать ошибки. Весьма тщательно проверив эти последовательные шаги, можете ли вы доверять окончательному заключению? Не более, а возможно и менее, чем окончательному результату длинного вычисления.
Действительно, математик, проверивший детали доказательства шаг за шагом и нашедший каждый шаг в порядке, всё же может быть неубеждён. Для убеждённости ему нужно нечто большее, чем правильность каждой детали. Что же?
Он хочет понять доказательство. После того как он пробился через доказательство, шаг за шагом, он берёт на себя больший труд: он пересматривает, перерабатывает, переформулирует и перерасполагает эти шаги до тех пор, пока ему не удаётся сгруппировать детали в доступное пониманию целое. Только тогда он начинает доверять доказательству.
Я не отважился бы анализировать, что составляет «понимание». Некоторые говорят, что оно основано на «интуиции», и ощущение целого и группировку деталей в хорошо упорядоченное гармоничное целое они приписывают интуиции. Я не отважился бы этому противоречить, хотя у меня есть некоторые опасения.7 Однако я хочу привлечь внимание к одному обстоятельству, на мысль о котором настойчиво наводят примеры и обсуждения в этой книге.
Некоторая практика может убедить нас, что аналогия и частные случаи могут быть полезны и в отыскании, и в понимании математических доказательств. С помощью аналогии могут быть подсказаны или сделаны более ясными общий план или значительные части доказательства. Доказательство могут подсказывать и частные случаи (см., например, § 3.17); с другой стороны, мы можем проверить уже сформулированное доказательство, наблюдая, как оно проходит в знакомых или критических частных случаях. Однако аналогия и частные случаи являются наиболее обильными источниками правдоподобных рассуждений: возможно, они не только помогают создавать доказательное рассуждение и делать его более понятным, но и увеличивают наше доверие к нему. И это заставляет нас подозревать, что значительная часть нашей уверенности в доказательных рассуждениях может проистекать из правдоподобных рассуждений.
| 1. | Oeuvres de Descartes, ed. Adam et Tannery, vol. 10, 1908, p. 204. назад к тексту |
| 2. | Параграфы 4, 5 и 6 с незначительными изменениями воспроизводят части моей статьи «With, or without motivation?», Amer. Math. Monthly, 56 (1949), |
| 3. | Меня можно извинить за то, что я выбрал пример из моей собственной работы. См. G. Pólya, Proof of an inequality, Proc. Lond. Math. Soc. (2), 24 (1925), 57. Доказанная теорема принадлежит Т. Карлеману. назад к тексту |
| 4. | Изложение, промежуточное между § 4 и § 6, см. в книге Г. Г. Харди, Дж. И. Литлвуд и Д. Пойа, Неравенства, М., 1948, |
| 5. | Муж английской королевы принадлежит к семье английских пэров, сменившей в 1917 г. свою немецкую фамилию Баттенберг на Маунтбэттен. |
| 6. | См. G. Pólya, Sur les types des propositions composées, Journal of Symbolic Logic, 5 (1940), |
| 7. | Значение интуиции и её роль в группировке деталей обычно не слишком хорошо объясняются. Замечательно, однако, что Декарт, от которого ведёт происхождение современное употребление термина «интуиция», оба эти момента объясняет довольно убедительно, в третьем и седьмом из своих правил для руководства ума. См. Рене Декарт, Избранные произведения, М., 1950, |