
476 Кб
 |
| 476 Кб |
В наши дни каждый, кто занимался математикой как профессионал или как любитель, слышал о диофантовых уравнениях и даже о диофантовом анализе. За последние 15–20 лет эта область сделалась «модной» благодаря своей близости к алгебраической геометрии — властительнице дум современных математиков. Между тем, о том, кто дал имя неопределённому анализу, о самом Диофанте, одном из наиболее интересных учёных античности, почти ничего не написано. О его работах даже историки науки имеют самое превратное представление. Большинство из них считает, что Диофант занимался решением отдельных задач, равносильных неопределённым уравнениям, применяя для этого хитроумные, но частные методы. Подробнее об этих оценках Диофанта мы скажем в §4.
Между тем простой разбор задач Диофанта показывает, что он не только поставил проблему решения неопределённых уравнений в рациональных числах, но и дал некоторые общие методы их решения. Надо при этом иметь в виду, что в античной математике общие методы никогда не излагались «в чистом виде», отдельно от решаемых задач. Так, например, поступал Архимед: определяя площади эллипса, сегмента параболы, поверхности шара, объёмы шара и других тел, он применял метод интегральных сумм и метод предельного перехода, однако нигде не дал общего абстрактного описания этих методов. Учёным XVI–XVII веков приходилось тщательно изучать и перелагать по-новому его сочинения, чтобы выделить оттуда методы Архимеда. Аналогично обстоит дело и с Диофантом. Его методы были поняты и применены для решения новых задач Виетом и Ферма,
Заметим ещё, что если история интеграционных методов Архимеда в основном завершается созданием интегрального и дифференциального исчисления Ньютоном и Лейбницем, то история методов Диофанта растягивается ещё на несколько сотен лет, переплетаясь с развитием теории алгебраических функций и алгебраической геометрии. Развитие идей Диофанта можно проследить вплоть до работ Анри Пуанкаре и Андре Вейля. Поэтому-то история диофантова анализа особенно интересна.
Настоящая книга будет посвящена в основном методам Диофанта для решения неопределённых уравнений второго и третьего порядка в рациональных числах и их истории. Попутно мы рассмотрим вопрос и о числовой системе, которую применял Диофант, и о его буквенной символике. В этом гораздо более простом вопросе также до сих пор нет ясности: большинство историков науки считает, что Диофант ограничивался областью положительных рациональных чисел и не знал отрицательных чисел. Мы постараемся показать, что это не так, что именно в «Арифметике» Диофанта область чисел была расширена до поля рациональных чисел Q.
Я надеюсь, что эта книга познакомит читателя с новой стороной античной математики. Ведь большинство из нас составляет о ней впечатление по «Началам» Евклида, сочинениям Архимеда и Аполлония. Диофант открывает нам мир арифметики и алгебры, не менее богатый и красочный.
Разумеется, мы не сможем рассказать здесь о всём творчестве Диофанта, ещё того менее, — о всём диофантовом анализе и его истории. Как мы уже говорили, мы будем следить в основном за той областью, которая получила название арифметики алгебраических кривых и которая состоит в нахождении рациональных точек алгебраической кривой (или рациональных решений одного алгебраического уравнения от двух переменных) и в изучении структуры этого множества. Поэтому читатель не найдёт здесь истории проблемы решения неопределённых уравнений в целых числах, которой занимались Ферма, Эйлер, Лагранж, Лежандр и которой продолжают заниматься и теперь. Мы не будем также касаться трудного и тонкого вопроса о существовании рационального (или целого) решения у неопределённого уравнения с целыми рациональными коэффициентами, поскольку этот вопрос выходит за пределы круга проблем, непосредственно идущих от Диофанта. Наконец, мы не будем касаться и истории десятой проблемы Гильберта, в которой требуется найти общий метод (или доказать, что такового не существует), «следуя которому можно было бы в конечное число шагов узнать, имеет данное уравнение решение в целых рациональных числах или нет» 1). Настоящая книга рассчитана на широкий круг читателей: её смогут прочесть преподаватели математики высших учебных заведений и школ, студенты физико-математических факультетов университетов и пединститутов, инженеры и школьники старших классов специализированных школ (с математическим уклоном). Строго говоря, для понимания книги достаточно знания аналитической геометрии и элементов дифференциального и интегрального исчисления, поэтому школьникам не все разделы будут доступны в равной степени. Чтобы облегчить пользование книгой, мы даём здесь «указатель», в котором расскажем, как книга построена и какие параграфы можно опустить без ущерба для понимания целого. В §1 рассказывается о самом Диофанте, в §2 — о системе чисел и символов, которые он вводит, в §3 приводятся сведения из диофантовых уравнений и алгебраической геометрии, необходимые для понимания дальнейшего. Следующий, §4, посвящён оценкам методов Диофанта историками математики. В §5 и §6 излагаются задачи Диофанта и исследуется, какими методами он решал неопределённые уравнения второго и третьего порядков. Здесь же рассказывается об однородных или проективных координатах. В §7 приводятся некоторые задачи Диофанта, которые потребовали теоретико-числового исследования. Эти задачи позволяют судить об объёме знаний античных математиков по теории чисел. Всё дальнейшее,
В заключение я приношу глубокую благодарность А. И. Лапину и И. Р. Шафаревичу, которым я обязана многими ценными замечаниями и указаниями.
Многие усовершенствования и поправки были внесены в рукопись редактором Н. Н. Гендрихсоном, которому я также приношу глубокую благодарность.
В конце книги помещён список наиболее доступных изданий «Арифметики» Диофанта и сочинений о ней.
Диофант представляет одну из наиболее трудных загадок в истории науки. Нам не известны ни время, когда он жил, ни предшественники его, которые работали бы в той же области. Труды его подобны сверкающему огню среди полной непроницаемой тьмы.
Промежуток времени, когда мог жить Диофант, составляет полтысячелетия! Нижняя грань этого промежутка определяется без труда: в своей книге о многоугольных числах Диофант неоднократно упоминает математика Гипсикла Александрийского, который жил в середине II века до н. э. С другой стороны, в комментариях Теона Александрийского к «Альмагесту» знаменитого астронома Птолемея помещён отрывок из сочинения Диофанта. Теон жил в середине IV века н. э. Этим определяется верхняя грань этого промежутка. Итак, 500 лет!
Французский историк науки Поль Таннери, издатель наиболее полного текста Диофанта, попытался су́зить этот промежуток. В библиотеке Эскуриала он нашёл отрывки из письма Михаила Пселла, византийского учёного XI века, где говорится, что «учёнейший Анатолий, после того как собрал наиболее существенные части этой науки (речь идёт о введении степеней неизвестного и об их обозначениях), посвятил их своему другу Диофанту». Анатолий Александрийский действительно составил «Введение в арифметику», отрывки из которой приводят в дошедших до нас сочинениях Ямблих и Евсевий. Но Анатолий жил в Александрии в середине III века н. э. и даже более точно — до 270 года, когда он стал епископом Лаодакийским. Значит, его дружба с Диофантом, которого все называют Александрийским, должна была иметь место до этого. Итак, если знаменитый александрийский математик и друг Анатолия по имени Диофант составляют одно лицо, то время жизни Диофанта — середина III века н. э.
Сама же «Арифметика» Диофанта посвящена «достопочтенному Дионисию», который, как видно из текста «Введения», интересовался арифметикой и её преподаванием. Хотя имя Дионисий было в то время довольно распространённым, Таннери предположил, что «достопочтенного» Дионисия следует искать среди известных людей эпохи, занимавших видные посты. И вот оказалось, что в 247 году епископом Александрии стал некий Дионисий, который с 231 года руководил христианской гимназией города! Поэтому Таннери отождествил этого Дионисия с тем, которому посвятил свой труд Диофант, и пришёл к выводу, что Диофант жил в середине III века н. э. Мы можем, за неимением лучшего, принять эту дату.
Зато место жительства Диофанта хорошо известно — это знаменитая Александрия, центр научной мысли эллинистического мира.
После распада огромной империи Александра Македонского Египет в конце IV века до н. э. достался его полководцу Птолемею Лагу, который перенёс столицу в новый город — Александрию. Вскоре этот многоязыкий торговый город сделался одним из прекраснейших городов древности. Размерами его превзошёл впоследствии Рим, но долгое время ему не было равного. И вот именно этот город стал на многие века научным и культурным центром древнего мира. Это было связано с тем, что Птолемей Лаг основал Музейон, храм Муз, нечто вроде первой Академии наук, куда приглашались наиболее крупные учёные, причём им назначалось содержание, так что основным делом их были размышления и беседы с учениками. При Музейоне была построена знаменитая библиотека, которая в лучшие свои дни насчитывала более 700 000 рукописей. Неудивительно, что учёные и жаждущие знаний юноши со всего мира устремились в Александрию, чтобы послушать знаменитых философов, поучиться астрономии и математике, иметь возможность в прохладных залах библиотеки углубиться в изучение уникальных рукописей.
Музейон пережил династию Птолемеев. В первые века
Тоньше другие ковать будут жизнью дышащую бронзу, —
Верю тому, — создадут из мрамора лики живые,
Красноречивее будут в судах, движения неба
Тростью начертят своей и вычислят звёзд восхожденья,
Ты же, римлянин, знай, как надо народами править 2).
И если в III–II веках до н. э. Музейон блистал именами Евклида, Аполлония, Эратосфена, Гиппарха, то в I–III веках н. э. здесь работали такие учёные как Герон, Птолемей и Диофант.
Чтобы исчерпать всё известное о личности Диофанта, приведём дошедшее до нас стихотворение-загадку:
Прах Диофанта гробница покоит; дивись ей — и камень
Мудрым искусством его скажет усопшего век.
Волей богов шестую часть жизни он прожил ребёнком
И половину шестой встретил с пушком на щеках.
Только минула седьмая, с подругою он обручился.
С нею пять лет проведя сына дождался мудрец;
Только полжизни отцовской возлюбленный сын его прожил.
Отнят он был у отца ранней могилой своей.
Дважды два года родитель оплакивал тяжкое горе,
Тут и увидел предел жизни печальной своей 3).
Отсюда нетрудно подсчитать, что Диофант прожил 84 года. Однако для этого вовсе не нужно владеть искусством Диофанта! Достаточно уметь решать уравнение
Но наиболее загадочным представляется творчество Диофанта. До нас дошло шесть книг из 13, которые были объединены в «Арифметику». Стиль и содержание этих книг резко отличаются от классических античных сочинений по теории чисел и алгебре, образцы которых мы знаем по «Началам» Евклида, его «Данным», леммам из сочинений Архимеда и Аполлония. «Арифметика», несомненно, явилась результатом многочисленных исследований, которые остались нам совершенно не известны. Мы можем только гадать о её корнях и изумляться богатству и красоте её методов и результатов.
«Арифметика» Диофанта — это сборник задач (их всего 189), каждая из которых снабжена решением (или несколькими способами решения) и необходимыми пояснениями. Поэтому с первого взгляда кажется, что она не является теоретическим произведением. Однако при внимательном чтении видно, что задачи тщательно подобраны и служат для иллюстрации вполне определённых, строго продуманных методов. Как это было принято в древности, методы не формулируются в общем виде, а повторяются для решения однотипных задач.
Всё же первой книге предпослано «общее введение» автора, на котором мы остановимся более подробно.
Диофант начинает с основных определений и описания буквенных символов, которые он будет применять.
В классической греческой математике, которая нашла своё завершение в «Началах» Евклида, под числом
Диофант приводит традиционное определение числа как множества единиц, однако в дальнейшем ищет для своих задач положительные рациональные решения, причём называет каждое такое решение числом
Но этим дело не ограничивается. Диофант вводит отрицательные числа: он называет их специальным термином
Заметим, что термин
Мы так подробно остановились на филологическом анализе текста Диофанта, чтобы убедить читателя, что мы не отступим от истины, если будем переводить термины Диофанта как «положительное» и «отрицательное».
Диофант формулирует для относительных чисел правило знаков:
|
«отрицательное, умноженное на отрицательное, даёт положительное, тогда как отрицательное на положительное даёт отрицательное, и отличительный знак для отрицательного есть |
Далее он пишет:
|
«После того как я тебе объяснил умножение, становится ясным и деление предложенных членов; теперь будет хорошо приступить к упражнениям над сложением, вычитанием и умножением таких членов. И положительные и отрицательные члены с различными коэффициентами прибавлять к другим членам, которые либо положительны, либо, равным образом, и положительны и отрицательны, и от положительных членов и других отрицательных отнимать другие положительные и, равным образом, положительные и отрицательные». |
Заметим, что хотя Диофант ищет только рациональные положительные решения, в промежуточных выкладках он охотно пользуется отрицательными числами.
Мы можем, таким образом, отметить, что Диофант расширил числовую область до поля рациональных чисел, в котором можно беспрепятственно производить все четыре действия арифметики.
В «Арифметике» мы встречаем впервые и буквенную символику. Диофант ввёл следующие обозначения для первых шести степеней x,
первая степень — ς;
вторая степень — Δυ̃ от
третья степень — Κυ̃ от
четвёртая степень — Δυ̃Δ от
пятая степень — ΔΚυ̃ от
шестая степень — Κυ̃Κ от
Свободный член, или x0, Диофант обозначал символом
| ° | |
| Μ | , |
т.е. первыми двумя буквами слова
Он ввёл специальный знак для отрицательного показателя степени Итак, у Диофанта была символика для обозначения одного неизвестного и его положительных и отрицательных степеней вплоть до шестой. Обозначения для второго неизвестного он не ввёл, что сильно затрудняло решение задач. Иногда на протяжении одной задачи Далее, Диофант излагает правила умножения xm на xn для положительных и отрицательных m и n Для равенства Диофант применял знак ΐσ — первые две буквы слова он записывает так:
Далее, во «введении» формулируются правила преобразования уравнений: прибавление равных членов к обеим частям уравнения и приведение подобных членов. Оба эти правила получили впоследствии широкую известность под арабизированными названиями «алджебр» и «альмукабала».
Мы видим, что хотя при наименовании и обозначении степеней неизвестного ещё применяются геометрические термины «квадрат», «куб» (что, кстати, сохранилось и до наших дней), однако при составлении уравнений Диофант спокойно складывает квадрат или куб со стороной 6), Таким образом, мы здесь встречаемся с совершенно новым построением алгебры, которая основывается уже не на геометрии, как это было у Евклида, а на арифметике. Однако это не простой возврат к числовой алгебре Вавилона, а начало построения буквенной алгебры, которая Но в «Арифметике» поражает не только совершенно новый язык, не только смелое расширение области чисел, но и особенно те проблемы, которые ставит и решает Диофант.
Чтобы понять сущность этих проблем и исследовать методы Диофанта, нам придётся дать некоторые сведения из алгебраической геометрии и теории неопределённых уравнений. В настоящее время задача решения неопределённых уравнений формулируется так: пусть дано m многочленов от n переменных, и определить его алгебраическую структуру. При этом решение Множество M(k), разумеется, зависит от поля k. Так, уравнение Наиболее важными для теории чисел являются случаи, когда Мы ограничимся рассмотрением только таких задач Диофанта, которые сводятся к одному уравнению с двумя неизвестными, Это уравнение определяет на плоскости R2 алгебраическую Прежде всего необходимо дать какую-нибудь классификацию уравнений (2) или, что то же, алгебраических кривых. Наиболее естественной и ранее всего возникшей является классификация их по порядкам.
Напомним, что порядком кривой (2) называется максимальный порядок членов многочлена Однако для целей диофантова анализа (такое название получила область математики, выросшая из задач решения неопределённых уравнений; впрочем, теперь её чаще называют диофантовой геометрией) классификация по порядкам оказалась слишком грубой. Поясним сказанное на примере. Пусть задана окружность Более тонкой является классификация алгебраических кривых по родам, которая была введена только в XIX веке Абелем и Риманом. Эта классификация учитывает число особых точек кривой Γ.
Будем считать, что в уравнении (2) кривой Γ многочлен где
fy' (x0, y0) Если в точке P производная Если же в точке P обе частные производные обращаются в нуль, то точка P называется особой.
Например, у кривой Наиболее простыми особыми точками являются двойные, в которых хотя бы одна из производных У алгебраической кривой может быть только конечное число особых точек. Действительно, пусть — уравнение кривой, где и уравнению (*). Но система этих трёх алгебраических уравнений может иметь только конечное число решений.
Мы определим здесь род для таких плоских алгебраических кривых, которые не имеют никаких особых точек, кроме двойных. В общем случае, Итак, пусть число двойных точек плоской алгебраической кривой Γ равно d 2 где n — порядок кривой Γ. Можно показать, что Если Γ — прямая или кривая второго порядка, то из приведённой формулы видно, что Однако и классификация по родам не учитывает арифметических свойств кривой. Так, например, кривые где φ и ψ — рациональные функции, Это уравнение определяет некоторую кривую Γ'. Для того чтобы рациональные точки кривой Γ, кроме, быть может, конечного числа их, переходили в рациональные точки где φ1 и ψ1 — рациональные функции с рациональными коэффициентами.
Если между двумя кривыми Γ и Γ' можно установить соответствие с помощью формул Так, например, если то u, v также выразятся через x, y линейно с рациональными коэффициентами, Покажем, что её можно бирационально преобразовать в кривую L' вида u (x – 1)2 Тогда уравнение (*) преобразуется в При этом x и y выражаются через u u2 и, обратно,
x – 1 (x – 1)2 т.е. кривые L и L' бирационально эквивалентны 9).
Множество рациональных точек M и M' двух бирационально эквивалентных кривых можно привести во взаимно однозначное соответствие, за исключением, быть может, конечного числа точек. Исключительными точками будут те, в которых числитель и знаменатель по крайней мере одной из функций (3) или (x – 1)2 С точки зрения диофантова анализа две бирационально эквивалентные кривые между собой равноправны. Между тем порядок Обратное утверждение неверно: кривые одного и того же рода могут не быть бирационально эквивалентными. Это видно хотя бы из приведённого выше примера кривых Таким образом, кривые одного и того же рода разбиваются на классы бирационально эквивалентных между собой кривых. Вся сила введённых понятий была выявлена в работах Анри Пуанкаре, который в самом начале XX века положил совокупность бирациональных преобразований в основу классификации и исследования проблем диофантова анализа. Мы будем говорить об этом в §12.
Сейчас отметим только один, весьма важный для дальнейшего, факт: если Γ — кривая третьего порядка, которая имеет по крайней мере одну рациональную точку, то её уравнение с помощью бирациональных преобразований всегда можно привести к виду где a и b — рациональные числа. Мы часто будем считать в дальнейшем, что кривая Γ уже задана в В следующих параграфах мы покажем, что Диофант владел общим методом для определения рациональных точек на кривых второго порядка. Как показал Пуанкаре, этот метод применим для всех кривых рода 0, имеющих рациональную точку. Диофант нашёл также общие методы для отыскания рациональных точек на кривых третьего порядка, причём методы эти оказались глубоко отличными от тех, которые он применял для кривых второго порядка. Из работ Пуанкаре следует, что эти методы Диофанта применимы для нахождения рациональных точек на любых кривых рода 1. Никаких других общих методов для нахождения рациональных точек алгебраических кривых до сих пор не существует.
Мы покажем также, какую роль сыграли идеи и методы Диофанта в истории математики, как ими пользовались математики от Виета и Ферма до Эйлера.
Между тем большинство историков науки, в противоположность математикам, до сих пор недооценивали труды Диофанта. Многие из них считали, что Диофант ограничивался нахождением только одного решения и применял для этого искусственные приёмы, различные для разных задач. Такого мнения придерживался, например, Г. Ганкель, который писал: «...современному математику после изучения 100 решений Диофанта трудно решить Но, может быть, такая оценка объясняется тем, что книга Ганкеля была написана до работ Пуанкаре, проливших новый свет на проблемы диофантовых уравнений? Но, вот, перед нами книга О. Беккера и И. Гофмана «История математики», вышедшая в 1951 году (O. Becker, J. Hofmann, Geschichte der Mathematik. Bonn). На стр. 90 мы читаем: «Диофант не даёт никакого общего метода, но применяет, Более правильную оценку Диофанта мы находим y Г. Г. Цейтена: «Вообще говоря, Диофант старается найти какое-нибудь одно решение задачи, не отыскивая общего решения её, которое включает в себя все возможные частные решения, но не следует придавать особенного значения этому факту, если желать понять полученные Диофантом результаты, ибо частные его решения заключаются лишь в том, что он сейчас же придаёт определённые значения вспомогательным количествам, служащим для решения задачи» (История математики в древности и средние века. После этого Цейтен разбирает способы Диофанта для решения неопределённых уравнений второго порядка. Однако и он не видит у Диофанта методов для решения неопределённых уравнений третьего порядка. До сих пор эти методы приписываются различным математикам нового времени. Так, Т. Сколем в своей книге «Диофантовы уравнения» (T. H. Skolem, Diophantische Gleichungen. Berlin, 1938) методы Диофанта приписывает Коши и Люка, а сам Люка — Коши и Ферма.
Итак, с общими методами решения неопределённых уравнений Диофанту так же не повезло, как и с отрицательными числами!
Но приступим к рассмотрению его задач. Два вида таких уравнений были рассмотрены до Диофанта. Это уравнения Второе полностью решается в «Началах» Евклида для случая Диофант в книге II своей «Арифметики» рассматривает различные неопределённые уравнения второго порядка и устанавливает, по существу, следующую теорему: неопределённое уравнение второго порядка от двух переменных либо не имеет ни одного рационального решения, либо имеет их бесконечно много, причём в последнем случае все решения выражаются как рациональные функции параметра где φ и ψ — рациональные функции.
Чтобы показать это, приведём сначала задачу 8 книги II.
«Данный квадрат разделить на два квадрата 10).
Пусть предложено 16 разделить на два квадрата. И положим первый x2, а другой тогда будет Образуем этот квадрат из нескольких x минус столько единиц, сколько содержится в Это равно
К обеим частям прибавим отрицательные (члены) и сделаем приведение подобных. Тогда Один будет 256/25, другой 144/25, сумма их будет Попробуем теперь выделить метод Диофанта «в чистом виде». Итак, пусть дано уравнение которое представляет окружность с центром в начале координат. Одним из рациональных решений этого уравнения будет Не имея обозначений для произвольного k, он берёт Подстановку (7) можно интерпретировать геометрически как проведение через точку Эта прямая встретит окружность (6) ещё в одной точке, координаты которой будут рациональными функциями от k. Действительно, и
k2 + 1 k2 + 1 Таким образом, каждому рациональному значению k отвечает одна и только одна рациональная точка Ещё яснее метод Диофанта виден из решения задачи 9 книги II, которую он формулирует так:
«Данное число, являющееся суммой двух квадратов, разбить на два других квадрата».
Диофант задаёт число 13, которое равно сумме Интересно отметить, что в качестве известной точки он берёт не указанную нами и имеющую положительные координаты, но выбирает точку с отрицательной ординатой, что соответствует отрицательному решению. Вообще Диофант в промежуточных выкладках охотно оперирует с отрицательными числами, хотя окончательное решение должно быть всегда рациональным и положительным.
Диофант применяет ту же процедуру и в задачах 16, 17 и других книги II.
Легко видеть, что метод Диофанта совершенно общий; он позволяет найти все рациональные точки кривой второго порядка, если эта кривая содержит хотя бы одну рациональную точку. Действительно, пусть дано уравнение второго порядка от двух переменных и пусть оно имеет рациональное решение и получим Но f2(x, y) = 0, поэтому C(a, b, k) Таким образом, для каждого рационального k мы найдём одно и только одно рациональное решение.
Если заданное уравнение имеет вид то Диофант несколько видоизменяет приём, полагая Тогда 2am – b Постараемся выяснить геометрический смысл этой второй подстановки. Для этого нам придётся перейти к однородным или проективным координатам. Поскольку эти координаты очень удобны для исследования свойств алгебраических кривых и мы будем неоднократно применять их в дальнейшем, остановимся на этом вопросе подробнее. До сих пор мы рассматривали, как это принято в аналитической геометрии, аффинную Установим теперь соответствие между точками плоскостей Если же z = 0, то точке Для перехода от уравнения записанного в аффинных координатах, к уравнению в однородных координатах полагаем z z Сделав соответствующую подстановку и приведение к общему знаменателю, получим уравнение где Φ(u, v, z) — многочлен относительно u, v и z. Например, уравнение гиперболы в однородных координатах примет вид Чтобы найти бесконечно удалённые точки этой кривой, положим Вернёмся к подстановке Диофанта. Уравнение (9) в однородных координатах запишется так: Точки Но наша точка лежит на этой Значит, можно положить или, снова переходя к аффинным координатам, получим Но это и есть подстановка, применённая Диофантом. Итак, она эквивалентна проведению произвольной прямой через рациональную бесконечно удалённую точку кривой (9).
Оговоримся сразу же, что мы вовсе не считаем, будто Диофант имел понятие о бесконечно удалённых точках кривой. Он просто пользовался эквивалентными соображениями. В истории математики нам известно немало примеров, когда основные факты некоторой теории были найдены до возникновения самой теории и до возникновения её основных понятий. Так было, например, с арифметикой квадратичных полей, которая была построена Эйлером, Лагранжем и Гауссом до введения квадратичных полей и даже до появления понятия алгебраического числа. Это было сделано в рамках теории квадратичных форм, но открытые там факты были эквивалентны арифметике квадратичных полей.
Так было и в «Арифметике» Диофанта, где некоторые общие предложения алгебраической геометрии были открыты и изучены, но без геометрической интерпретации, в рамках чистой алгебры и теории чисел.
Зададимся теперь вопросом, знал ли Диофант, что число решений поставленных им задач бесконечно? Или он, действительно, довольствовался нахождением одного рационального решения?
В книге II он ничего не говорит об этом и бесконечность решений можно усмотреть только из метода Диофанта. Однако в задаче 19 книги III он пишет: «мы уже знаем, что заданный квадрат можно разбить на два квадрата бесконечным числом способов». Далее, задачу 19 книги IV Диофант формулирует так:
«Найти общие (или неопределённые) выражения для трёх чисел таких, что произведение любых двух из них вместе с единицей давало бы квадрат».
Диофант находит эти выражения в виде «Итак, проблема решена с помощью общих выражений (или в неопределённом виде), так что произведение любых двух из них вместе с единицей даёт квадрат, как бы ни было выбрано x. Ибо найти общие (или неопределённые) выражения означает дать такую формулу, что, каково бы ни было значение x, после его подстановки удовлетворяются условия (задачи)».
Заметим, что методы Диофанта для решения неопределённых уравнений совпадают с так называемыми «подстановками Эйлера», которые хорошо известны каждому, изучавшему математический анализ. И там и тут x и y выражаются с помощью рациональных функций от одного параметра; делается это с помощью одних и тех же подстановок, только при вычислении интеграла √ax² + bx + c нам не нужно требовать, чтобы коэффициенты этих функций сами были рациональными числами. Поэтому можно положить У Диофанта же, поскольку речь шла о рациональных точках, все подстановки должны были иметь рациональные коэффициенты. Поэтому ему приходилось учитывать это добавочное требование. В книге IV Диофант рассматривает неопределённые уравнения третьего и четвёртого порядков. Здесь дело обстоит гораздо сложнее: если кривая третьего порядка и имеет рациональные точки, то координаты их, вообще говоря, не могут быть выражены рациональными функциями одного параметра. Однако, зная одну или две рациональные точки кубической кривой, можно найти ещё одну её рациональную точку. Действительно, любая прямая пересекает кривую третьего порядка в трёх точках, координаты которых можно найти например, из уравнения третьей степени, получающегося и прямой. Если два корня этого результирующего уравнения рациональны, то и третий будет рациональным (это можно усмотреть хотя бы из того, что сумма корней кубического уравнения равна коэффициенту 1) если P — рациональная точка 2) Если P1 и P2 — рациональные точки В дальнейшем будем называть эти способы методами касательной и секущей Диофанта. Покажем, что мы имеем право приписать оба эти метода Диофанту. Для этого рассмотрим его задачи.
Задача 24 книги IV:
«Данное число разбить на два числа так, чтобы их произведение было равно кубу без стороны.
Пусть дано 6. Я полагаю 1-е число x, тогда Это равно Если коэффициенты при x в обеих частях были бы равны, то остались бы равные члены с x3 и x2; тогда x было бы рациональным. Но 4x получается как избыток Так как я хочу, чтобы и
По формулам: Постараемся теперь выделить метод Диофанта в чистом виде. Пусть задано Одним из рациональных решений будет (Диофант берёт сначала Для того чтобы x получилось рациональным, достаточно положить что и делает Диофант. После этого найдём k3 a3 Посмотрим, что означает или
Тогда Но f3(a, b) = 0 и, если положить
то получим B(a, b) ∂x ∂y т.е. угловой коэффициент нашей прямой (12) должен быть выбран так, чтобы она была касательной к Этим же способом Диофант решает задачу 18 книги VI, а также, вероятно, и задачу рассмотренную, по свидетельству самого Диофанта, в его книге «Поризмы», которая до нас не дошла.
Заметим, что попутно Диофант получает чисто алгебраический способ определения углового dx ∂x ∂y Этот способ, который не требует предельного перехода, Перейдём теперь к задаче 26 книги IV, где применяется метод секущей.
«Найти два числа, произведение которых вместе с каждым из них будет кубом.
Положим первое x с каким-нибудь коэффициентом, равным кубу, Остаётся сделать так, чтобы при прибавлении к тому же второго тоже получался куб. Но прибавление второго даёт Образуем куб из Обозначим, следуя Диофанту, первое неизвестное через a3x, второе через Диофант делает подстановку 3a2 + 1 Остановимся несколько подробнее на применённом здесь методе. Одним из рациональных решений Диофант приравнивает нулю не коэффициент при x, как это имело место в предыдущем случае, а коэффициент при x3 и получает Что означает такое приравнивание с геометрической точки зрения? Для выяснения этого вопроса запишем уравнение (15) в однородных координатах, положив Мы видим, что эта кривая имеет две рациональные точки Она-то и даёт в пересечении Диофант применяет свои методы касательной и секущей и в других задачах книг IV, V и VI. В тех книгах «Арифметики», которыми мы располагаем, исследования по теории чисел, в собственном смысле слова, отсутствуют. Однако, ставя некоторые задачи или решая их, Диофант иногда формулирует, при каких условиях эта задача возможна или невозможна 12), или отмечает, что некоторое полученное в процессе решения число невозможно представить в том или ином виде, например, как сумму двух квадратов. Именно таким образом и появляются в «Арифметике» теоремы теории чисел. Судя по одному замечанию самого Диофанта все эти и другие теоремы такого рода были им рассмотрены в специальной книге «Поризмы», которая до нас не дошла.
Поэтому нам ничего другого не остаётся, как судить о знаниях Диофанта в теории чисел на основании замечаний и диоризмов, имеющихся в «Арифметике». Начнём с задачи 19 книги III.
«Найти четыре числа такие, чтобы квадрат суммы их, если к нему прибавить одно из них, или отнять, оставался бы квадратом.
Так как во всяком прямоугольном треугольнике, если к квадрату гипотенузы прибавить или из него отнять удвоенное произведение сторон, заключающих прямой угол, получится квадрат, то я ищу сперва четыре прямоугольных треугольника, имеющих равные гипотенузы. Это то же, что разбить некоторый квадрат на два квадрата (четырьмя способами), а мы уже знаем, что Итак, пусть предложены два прямоугольных треугольника в наименьших числах, как 3, 4, 5 и 5, 12, 13. Умножим каждый из предложенных на гипотенузу другого; тогда первый треугольник будет 39, 52, 65, а второй 25, 60, 65. Это и есть прямоугольные треугольники, имеющие равные гипотенузы.
По своей природе 65 может быть разложено на два квадрата двумя способами: на 16 и 49, и Теперь от предложенных 49 и 16 я беру стороны, они будут 7 и 4, и образую из двух чисел 7 и 4 прямоугольный треугольник Подобным образом 64 и 1 имеют стороны 8 и 1, и я образую из них другой прямоугольный треугольник, стороны которого будут И вот получены четыре прямоугольных треугольника, имеющих равные гипотенузы. Итак, вернёмся к первоначальной задаче; я полагаю сумму четырёх (чисел) Тогда сумма четырёх чисел что даёт
По формулам будут с одним и тем же знаменателем Эта задача замечательна во многих отношениях. о котором мы говорили в §5. Наиболее общие формулы для его решения привёл Евклид в «Началах». Диофант без специальных оговорок пользуется этими формулами, дающими при взаимно простых p и q все целые решения этого уравнения, не имеющие общего делителя: (Поскольку уравнение однородно, то расширение области решения до поля рациональных чисел не даёт тут ничего нового.) Эти решения можно получить тем же методом, который Диофант применил в задаче 8 книги II для разложения заданного квадрата в сумму двух квадратов (см. §5).
Во-вторых, она содержит утверждение, что произведение двух целых чисел, каждое из которых является суммой двух квадратов, само представимо суммой двух квадратов и притом по крайней мере двумя различными способами (если только перемножаемые числа не равны между собой). При этом, если Именно в примечаниях к этой задаче Ферма высказал своё знаменитое утверждение, что каждое простое число вида Были ли известны эти предложения Диофанту? Для ответа на этот вопрос рассмотрим ещё одну задачу Диофанта, снабженную диоризмом, говорящим о представимости некоторого числа суммой двух квадратов — задачу 9 книги V.
«Разделить единицу на две дроби так, чтобы прибавление к каждой из частей заданного (числа) делало бы его квадратом».
Вслед за условием Диофант формулирует ограничение (диоризм), которое надо наложить на заданное число, чтобы задача была возможной. К сожалению, после слов: «Необходимо, чтобы заданное число не было бы нечётным и чтобы удвоенное от него и «Пусть предложено к каждой части прибавить 6 так, чтобы получились квадраты.
Так как мы хотим разбить 1 на такие части, чтобы при прибавлении к каждой из них 6 Если теперь я разобью 13 на два квадрата, разность которых Всё на x2. Получаем Итак, x2 = 100, Значит, прибавляемое к 26 будет Итак, необходимо разбить 13 на два квадрата, построив для каждого сторону, приближенно равную Итак, я образую два квадрата, один из и получим x = 5/101.
Значит, будет сторона одного квадрата Условия задачи мы можем записать в виде системы трёх уравнений: Складывая два последние уравнения, получим Поэтому число a должно быть выбрано так, чтобы «Если число после деления на наибольший содержащийся в нём квадрат даёт частное, которое делится на простое число вида Эти условия могут быть выведены из одной замечательной теоремы, которую сформулировал Ферма, а доказал Эйлер, а именно: суммой двух квадратов представимы те и только те простые числа, которые имеют Знал ли Диофант доказательство своего диоризма и подозревал ли он о том, что выставленные им условия не только необходимы, но и достаточны для представимости целого числа суммою двух квадратов?
Этому вопросу посвятил специальное исследование один из знаменитых математиков XIX века, младший современник Гаусса, Карл Густав Якоб Якоби (1804–1851). Прежде всего, он провёл тщательный филологический анализ текста Диофанта и предложил следующую его реконструкцию:
«Необходимо, чтобы заданное число не было нечётным, и чтобы удвоенное его и единица не имело делителя, кратного четырём без единицы».
Примерно так же этот текст был впоследствии восстановлен большим знатоком античности и издателем Диофанта Полем Таннери (издание 1893 года).
Это условие действительно будет необходимо, если к нему прибавить оговорку «после деления на наибольший содержащийся в нём квадрат», но, по-видимому, Диофант подразумевает это. В таком случае условие будет и достаточным, Якоби полагает, что Диофант имел доказательство того, что высказанное им условие является необходимым, Якоби не сомневается в том, что Диофант знал и о достаточности своих условий, однако не мог этого доказать, так как для этого нужны были средства, выходящие за пределы античной математики.
В задаче 14 книги V Диофант сформулировал условие, необходимое для того, чтобы некоторое число могло быть представлено суммой трёх квадратов. Диоризм заключается в том, что число не должно иметь вид Комментировать Диофанта начали ещё в древности. Разбору его книг были посвящены труды знаменитой Гипатии, дочери александрийского учёного Теона. Гипатия жила в Сочинения Гипатии до нас, к сожалению, не дошли.
После Гипатии мы не знаем ни одного александрийского математика. Последние греческие учёные Прокл, Исидор и Симпликий развивали своё учение уже не в Александрии, а в Афинах. Но и здесь к началу VII века научная мысль угасла. Античная наука погибла вместе с гибелью античного общества. В IX–XIII веках возникли новые научные центры: Константинополь, а также Багдад и другие города арабского Востока. Отсюда начиная с XII века научная мысль проникала в Европу. Идеи Диофанта шли двумя различными потоками. Первый из них можно назвать алгебраическим, второй — теоретико-числовым или арифметическим. При этом то новое, что внёс Диофант в алгебру, стало известно учёным Европы лет на 300 раньше, чем его арифметические идеи. Это и неудивительно. Новая алгебра и была воспринята как византийскими комментаторами Диофанта (Максим Плануда, Георгий Пахимер, жившие в XIII веке), так и арабскими математиками, особенно Абуль Вафой (X век) и его школой. Правда, арабы не пользовались буквенными символами, а именовали степени неизвестного словами. Кроме того, при наименовании степеней неизвестного они пользовались не аддитивным принципом, как это делал Диофант, а неудобным мультипликативным, Что касается правил Диофанта оперирования с многочленами и уравнениями, то они повторялись почти всеми алгебраистами средних веков.
Отрицательные числа были восприняты гораздо менее охотно. Арабские математики вообще от них отказались, а европейцы принимали их с большим недоверием. Долгое время они именовали отрицательные числа «ложными числами» и старались обходиться без них.
Но в «Арифметике» Диофанта имелся и другой, гораздо более глубокий круг идей, связанный с решением неопределённых уравнений, с диофантовым анализом. Долгое время о них ничего не знали. В XV–XVI веках в Европе сложилась несколько парадоксальная ситуация: учёные пользовались буквенной алгеброй, восходящей к Диофанту, развивали её дальше, но не были знакомы с трудами Диофанта.
Первым прочёл их, по-видимому, известный астроном XV века Региомонтан (Иоганн Мюллер). Путешествуя по Италии, он открыл рукопись Диофанта в Венеции и сообщил об этом в письме к своему другу. Рукопись поразила его богатством содержания. Он решил перевести её, но не раньше, чем найдёт все 13 книг, о которых пишет Диофант во Введении. Однако, были найдены только 6 книг, те, которые известны и нам, и перевод так и не был сделан.
Прошло ещё 100 лет. За это время ни один из крупных алгебраистов, а их было немало, — достаточно назвать Джироламо Кардано и Николо Тарталья, ничего не знали о Диофанте. Но вот в 1572 году в «Алгебре» Рафаэля Бомбелли, профессора университета в Болонье, вдруг появляются 143 задачи из «Арифметики» Диофанта! В предисловии Бомбелли пишет, что «в прошлом году труд, посвящённый этому предмету, был найден в библиотеке Господа нашего в Ватикане, составленный неким Диофантом, греческим автором, жившим в эпоху Антонина Пия». Заметим, что Антонин Пий был Римским императором в середине II века н. э. Откуда взял своё утверждение о времени жизни Диофанта Бомбелли, абсолютно не известно. Прочтя рукопись, Бомбелли убедился, что автор её «весьма сведущ в науке чисел». И вот «с целью обогатить мир произведением такой важности» Бомбелли принялся совместно с римским математиком Пацци, который первый обнаружил рукопись, за перевод. «Мы перевели пять книг из семи, — сообщает Бомбелли, — но не смогли окончить остальное «Алгебра» Бомбелли замечательна во многих отношениях. Здесь были усовершенствованы алгебраические обозначения для степеней неизвестного, здесь впервые появились мнимые числа Но уже через три года после выхода в свет «Алгебры» был опубликован первый перевод «Арифметики» на латынь. Он был выполнен известным филологом и философом того времени Ксиландром (настоящее имя его — Гильом Хольцман). Перевод этот был, в целом, хорош, хотя чувствовалось, что он был выполнен человеком, далёким от математики.
После этого задачи четырёх первых книг Диофанта появились в книге известного математика и механика Симона Стевина (1585 год), а во втором издании, подготовленном талантливым алгебраистом Альбером Жираром, — и задачи из последних двух книг.
Но методы Диофанта обрели новую жизнь только в произведениях двух крупнейших математиков Франции XVI–XVII веков — Франсуа Виета и Пьера Ферма. Франсуа Виет (1540–1603) по праву считается родоначальником буквенного исчисления, до создания которого говорить об алгебре можно только с известными оговорками. Он первый после Диофанта сделал существенно новый шаг в построении такого исчисления и именно тем, что ввёл символы для произвольных постоянных величин (или параметров), фигурирующих в задачах. Только после этого появились первые алгебраические формулы и стало возможным часть умственных операций заменить буквенными.
Франсуа Виет был также первым математиком Европы, обратившим внимание на метод Диофанта для нахождения рациональных точек кубической кривой и хорошо понявшим этот метод.
В задаче 12 книги V Диофант пишет: «а мы имели в Поризмах, что разность любых двух кубов есть сумма двух кубов». Очевидно, речь идёт о решении уравнения где a>b>0 и x, y — положительные. Однако, решение этой задачи в самой «Арифметике» отсутствует.
В своей книге, носящей странное название «Зететика», — слово, придуманное автором для обозначения науки о приведении различных проблем к уравнениям, — Виет ставит ещё две аналогичные задачи:
1) x3 – y3 = a3 + b3 2) x3 – y3 = a3 – b3 Все три задачи он решает с помощью метода касательной Диофанта. Так, например, для решения и получает после подстановки Затем он требует, чтобы a3 + b3 Аналогично решаются и две другие задачи.
Впоследствии Ферма добавил к трём задачам Виета ещё одну, Она вызывала затруднения, так как при её решении обычным способом либо x либо y получаются отрицательными, В 1621 году Баше де Мезириак выпустил новое издание «Арифметики» Диофанта. Впервые был опубликован не только перевод на латынь (сделанный заново и имеющий значительные преимущества по сравнению с переводом Ксиландра), но и греческий текст. Однако это издание стало знаменитым не только благодаря качеству перевода и обстоятельным комментариям Баше, — на одном из его экземпляров Пьер Ферма записывал свои мысли и результаты, относящиеся к теории чисел. Именно здесь, на полях напротив задачи 8 книги II, в которой Диофант раскладывает заданный квадрат в сумму двух квадратов (см. §5), Ферма записал: «Наоборот, невозможно разложить куб на два куба, биквадрат на два биквадрата и вообще никакую степень, бо́льшую квадрата, на две степени с тем же показателем. Я дал этому поистине чудесное доказательство, но поля книги слишком узки для него». Это и есть знаменитая Большая или Великая теорема Ферма, прославившая имя своего автора далеко за пределами математики. Но и в самой нашей науке Великая теорема сыграла совершенно исключительную роль. Она служила предметом раздумий и исследований для Эйлера, Лежандра, Дирихле, Куммера и других крупнейших математиков и побудила их к построению новой области математики — высшей арифметики или арифметики полей алгебраических чисел.
Но кто же был автором Великой теоремы? Что мы о нём знаем? Несколько больше, чем о Диофанте, но гораздо меньше, чем о других его современниках.
Пьер Ферма родился в 1601 году на юге Франции близ Тулузы в зажиточной семье, принадлежащей к третьему сословию. Ферма получил хорошее образование: он прекрасно владел латынью, итальянским и испанским, причём писал на этих языках и по-французски изящные стихи. Греческий он знал настолько хорошо, что делал поправки ко многим учёным переводам (в том числе и к переводу Диофанта) и мог бы прославиться как знаток эллинизма. Получив юридическое образование, Ферма занял место советника Парламента Ферма бесспорно был первым математиком своего времени. Он создал наиболее общие новые методы той части нашей науки, которая получила название анализа бесконечно малых, наряду с Декартом он был творцом аналитической геометрии, вместе с Паскалем заложил основы теории вероятностей. Как и все учёные его времени, Ферма живо интересовался приложениями математики к анализу явлений физического мира. Он занимался оптикой, где с помощью принципа минимума, носящего теперь его имя, сумел объяснить, как движется луч света в неоднородной среде.
Но любимой областью Ферма была теория чисел. И здесь он не имел себе равных. Он сумел выбрать среди множества интересных вопросов и частных задач те основные проблемы, исследование которых и создало теорию чисел как науку. Проблемами Ферма занимались все крупные математики XVIII и XIX веков, от Эйлера и до Гильберта.
Мы говорим о «проблемах», а не о «теоремах», потому что большинство утверждений Ферма дошло до нас без доказательств: они сформулированы либо на полях его экземпляра «Арифметики» Диофанта, либо в письмах, где предлагается другим учёным попробовать свои силы для их обоснования. Исключение составляет только Великая теорема для биквадратов, доказательство которой он записал. Зато Ферма подробно описал новый общий метод доказательства теоретико-числовых предложений, который сам он назвал «методом бесконечного или неопределённого спуска». Приведём выдержку из письма Ферма, в которой он описывает новый метод:
«...Поскольку обычные методы, которые изложены в книгах, недостаточны для доказательства столь трудных предложений (Речь идёт о теоремах теории чисел. Я назвал этот способ доказательства бесконечным или неопределённым спуском; вначале я пользовался им только для доказательства отрицательных предложений, как-то:
что не существует числа, меньшего на единицу кратного трёх, которое составлялось бы из квадрата и утроенного квадрата;
что не существует прямоугольного треугольника в целых числах, площадь которого была бы квадратным числом. Доказательство проводится путём приведения к абсурду таким способом:
Если бы существовал какой-нибудь прямоугольный треугольник в целых числах, который имел бы площадь, равную квадрату, то существовал бы другой треугольник, меньший этого, который обладал бы тем же свойством. Если бы существовал второй, меньший первого, который имел бы это же свойство, то существовал бы в силу подобного рассуждения третий, меньший второго, который имел бы то же свойство, и, наконец, четвёртый, пятый, спускаясь до бесконечности. Но если задано число, то не существует бесконечности по спуску меньших его (я все время подразумеваю целые числа). Откуда заключают, что не существует никакого прямоугольного треугольника с квадратной площадью» 13).
Заметим, что предложение о площади прямоугольного треугольника, стороны которого выражаются в целых числах, на примере которого Ферма демонстрирует свой метод, равносильно тому, что не существует двух биквадратов, разность которых была бы квадратом. Значит, тем более эта разность не может быть биквадратом. Таким образом, из этого предложения следует Великая теорема для биквадратов. Доказательство этого предложения, выполненное методом спуска, до нас дошло. Это и есть единственное теоретико-числовое доказательство Ферма, которым мы располагаем. Впоследствии с помощью метода спуска Эйлер доказал Великую теорему для В наши дни метод спуска Ферма сделался незаменимым орудием при исследовании проблем диофантова анализа. Однако применение этого метода к проблемам, относящимся к рациональным точкам кривой или некоторого другого многообразия, потребовало введения нового понятия «высоты точки».
Пусть, например, дано неопределённое уравнение относительно которого требуется доказать, что оно не имеет решений в рациональных числах. Для доказательства перейдём к однородным координатам, положив z z получим Каждому рациональному решению (*) отвечает решение (**) в целых числах. Поэтому достаточно показать, что Так, например, если уравнение (*) имеет вид то уравнение (**) будет
Пусть теперь u, v, z — Нам остаётся рассказать о трактовке неопределённых уравнений второго и третьего порядков в работах Ферма. Самое большее, что можно здесь утверждать, сводится к следующему: Ферма хорошо понял Диофанта и умело применял его методы, к которым он добавил только сдвиг кривой. Задачи, сводящиеся к нахождению рациональных решений неопределённых уравнений третьего порядка, встречаются как на полях экземпляра «Арифметики», принадлежавшего Ферма, так и в сочинении де Бильи, написанного после смерти Ферма с целью разъяснить методы последнего. В этом сочинении, озаглавленном «Новое искусство» (Inventum novum), которое было присоединено к собранию трудов Ферма (это сделал Поль Таннери), методы Диофанта применяются обстоятельно и методически, однако ничего нового к ним не добавлено. Первый этап развития учения о неопределённых уравнениях второго и третьего порядков, начало которому положил Диофант, нашёл своё завершение в работах Леонарда Эйлера (1707–1783).
Величайший математик XVIII века, один из первых петербургских академиков, Леонард Эйлер занимает в нашей науке столь большое место, что буквально нельзя найти такую область математики, в которой ему не принадлежали бы фундаментальные результаты, глубокие идеи или мощные общие методы. Что касается рассматриваемого нами вопроса, то воздействие работ Эйлера было двояким. Сам он в своей «Алгебре» 14) систематически рассмотрел вопрос о решении в рациональных числах неопределённых уравнений вида и
и чётко сформулировал, в чём заключается различие между обоими случаями. Так, переходя к исследованию уравнений (17), Эйлер пишет:
«Мы должны заметить заранее, что здесь нельзя найти общего решения, как это было в предыдущих случаях, и метод, употребляемый ниже, приводит не к бесчисленному множеству решений одновременно, но теперь каждая операция позволяет нам узнать только одно значение x».
И он показывает, как найти новое решение при помощи метода касательной Диофанта. При этом все рассуждения проводились чисто аналитически, без применения каких бы то ни было геометрических терминов.
Эйлер заметил 15), что кривые третьего порядка в частных случаях могут вести себя как кривые второго порядка, Сам Эйлер доказал только достаточность этого условия: он показал, что в этом случае рациональные выражения для x и y можно найти при помощи подстановки Применяя указанную подстановку, получим откуда
a a Нетрудно показать, что условие Эйлера равносильно тому, что кривая определяющих особые точки, получим, что абсцисса двойной точки должна быть общим корнем многочлена Впоследствии Пуанкаре показал, что условие Эйлера не только достаточно, но и необходимо (см. §12).
В последние годы жизни Эйлер вновь обратился к диофантову анализу. Он усовершенствовал свои методы и впервые применил метод секущей Диофанта в случае, если известны две конечные рациональные точки тогда Эйлер полагал
β – α α – β что равносильно проведению прямой через точки β – α Для этого нужно только учесть равенства (18).
Эти работы были опубликованы только в 1830 году после смерти Эйлера.
Но Эйлеру принадлежат и другие исследования, с первого взгляда как будто не связанные с задачами Диофанта, но именно они внесли в трактовку этих задач совершенно новую точку зрения. Мы имеем в виду знаменитую теорему сложения эллиптических интегралов, открытую Эйлером.
Пусть дана кривая и точка A(x, y) на ней. Обозначим
y Теорема Эйлера утверждает, что для любых точек При этом координаты Вторая теорема Эйлера утверждает, что если задано уравнение где A и D — точки кривой Γ, а n — любое целое число, положительное или отрицательное, то координаты точки D рационально выражаются через координаты точки A.
В частности, если n = 2, то получаем уравнение Соотношение (21) называют иногда теоремой умножения эллиптических интегралов.
Если теперь точки A и B рациональные, то рациональными будут точки C и D, Эту-то связь теоремы сложения с диофантовым анализом и отметил впервые знаменитый немецкий математик Карл Густав Якоб Якоби. Он это сделал в своей статье «О применении теории эллиптических и абелевых интегралов в диофантовом анализе» (De usu theoriae integralium ellipticorum et integralium abelianorum in analysi Diophańtea), которая была опубликована в журнале Крелля, самом солидном немецком математическом журнале XIX века, в 1834 году. Современные Якоби учёные, В начале статьи Якоби высказывает удивление, что учёный муж где m1, ..., ms — любые целые числа. Аналогично, исходя из одной рациональной т.е. через конечное число шагов мы вернёмся к исходной точке. Якоби отмечает это и находит условие, при котором такое равенство будет иметь место (мы не будем приводить это условие, так как нам пришлось бы углубиться в изучение периодов интегралов В конце статьи Якоби намечает, как перенести полученные результаты на случай алгебраических кривых высших порядков. При этом вместо теоремы сложения Эйлера он пользуется более общими теоремами Абеля. Мы не будем здесь на этом останавливаться, отметим только, что эти идеи Якоби получили развитие только в наши дни.
Вернёмся к основному содержанию статьи. Покажем, что в ней Якоби близко подошёл к открытию структуры множества рациональных точек эллиптической кривой. Для такого открытия ему недоставало не аппарата, которым он прекрасно владел, но совершенно новой точки зрения, которая только постепенно и с трудом пробивала себе дорогу в XIX веке. Попробуем пояснить суть этой точки зрения. Рассмотрим Условимся считать точку C «суммой» точек A и B и писать Мы обвели знак + кружочком, чтобы подчеркнуть, что речь здесь идёт не о сложении чисел.
Итак, во множестве M мы определили закон композиции (операцию), который каждым двум элементам A и B из M ставит в соответствие третий элемент C из M.
В современной математике множество S, в котором определён закон Для любых трёх элементов A, B и C из S (ассоциативность).
В множестве S существует нейтральный элемент N — такой, что для Для каждого элемента A существует обратный (или противоположный) элемент A' Если, кроме того, для любых элементов из S то группа называется коммутативной или абелевой.
Так, множество всех целых чисел образует абелеву группу по сложению, множество рациональных положительных чисел — абелеву группу по умножению, множество квадратных матриц второго порядка, определители которых отличны от нуля, образует некоммутативную группу по умножению. В последнем случае роль нейтрального элемента играет единичная матрица.
Обычно, по аналогии с числовыми операциями, законы композиции в произвольных группах также называют сложением или умножением. В соответствии с этим нейтральный элемент называют нулём или единицей. (При этом становятся естественными названия противоположного или обратного элементов.)
Посмотрим, будет ли группой наше множество точек M с введённой операцией сложения.
Что касается первого условия, т.е. свойства ассоциативности, то оно следует из аналогичного свойства сложения интегралов, для которых, разумеется, Но существует ли во множестве M точка, которая играет роль нуля? И имеется ли для каждой точки этого множества «противоположная» точка?
Начнём с нуля. Если M — множество рациональных точек Теперь мы сможем для любой точки A найти «противоположную». Действительно, естественно считать, что Но тогда за A' нужно принять точку, симметричную –y y Заметим, что т.е. а значит, наша группа коммутативна.
Итак, исходя из теорем Эйлера и на основании связи, замеченной Якоби, можно было бы определить сложение во множестве рациональных точек эллиптической кривой, дополнив его только одной точкой, и тогда это множество получило бы структуру коммутативной группы. Точки конечного порядка, о которых говорит Якоби, являются элементами конечного порядка этой группы (элемент группы называется элементом конечного порядка, если некоторое Таков перевод замечаний Якоби на современный нам язык.
Однако, поскольку математики первой половины XIX века не были склонны переносить арифметические операции на точки или другие объекты, далёкие от чисел, то Якоби выражал те же результаты иначе. Вместо «сложения» точек A и B, он говорил о сложении интегралов Поставим теперь вопрос: имеет ли связь теорема сложения Эйлера с методами касательной и секущей Диофанта? Ведь в обоих случаях по двум или одной рациональной точке кривой Γ определяются новые её рациональные точки. Ни Эйлер, ни Якоби ничего не говорят об этой связи. А между тем такая связь имеется!
Уточним поставленный нами вопрос. По двум точкам A и B С другой стороны, проведём через A и B прямую и найдём её точку Теперь мы можем придать операции сложения точек на кривой простой геометрический смысл: суммой Однако, этим способом мы не можем сложить Какая же точка при такой интерпретации сложения точек будет играть роль нуля?
Для ответа на этот вопрос перейдём, как это мы делали в §6, к однородным координатам. Положим z z тогда уравнение (19) примет вид Из уравнения (19') видно, что при Условимся теперь считать, что набору чисел Покажем, что точка O и будет играть роль нуля. Для этого заметим, что все вертикальные прямые Пусть теперь дана некоторая рациональная Эта прямая пересечёт кривую Γ в трёх точках: Наконец, точкой, противоположной точке A, будет Заметим, что определённая нами точка O такова, что для неё
y Таким образом, и из теоремы сложения Эйлера можно было бы усмотреть, что роль нуля должна играть бесконечно удалённая точка.
Итак, «сложение» точек эллиптической кривой можно определить из процедур Диофанта. Знали ли об этом Эйлер и Якоби? Точнее, знали ли они, что три точки лежат на одной прямой? Ни Эйлер, ни Якоби не упоминают об этом, хотя по крайней мере Якоби этот факт должен был быть хорошо известен. Возможно, что о нём знал и Эйлер. Но, не выделяя специально случая кривой третьего порядка. А для Как ни просты изложенные здесь соображения о «сложении» точек эллиптической кривой, прошло ещё около 70 лет прежде, чем они были положены в основу систематического изучения структуры множества её рациональных точек. Это было сделано в начале XX века замечательным французским математиком Анри Пуанкаре (1854–1912). Работа Якоби, о которой мы говорили, осталась незамеченной и к идее построения арифметики на эллиптической кривой обратился только Пуанкаре. Однако за время, прошедшее между 1834 годом и концом XIX века, было много сделано в изучении геометрии алгебраических кривых. Ещё в работах замечательного норвежского математика Нильса Хенрика Абеля (1802–1829) появилось понятие рода алгебраической кривой 18). Из других соображений к тому же понятию пришёл крупнейший математик Германии Бернгард Риман (1826–1866). В своей знаменитой работе «Теория абелевых «Станем считать принадлежащими к одному классу все неприводимые алгебраические уравнения между двумя величинами, переводящиеся одно в другое посредством рациональных подстановок; итак, уравнения В последующих работах Клебша и других немецких математиков были заложены основы теории алгебраических кривых. Однако, как правило, такие кривые рассматривали над полем комплексных чисел Анри Пуанкаре начинает свой мемуар «Об арифметических свойствах алгебраических кривых» 20) с важного замечания, что арифметические свойства многих объектов самым тесным образом связаны с преобразованиями этих объектов: так, например, если речь идёт о квадратичных формах от двух переменных, то, как показал Гаусс, такими преобразованиями будут линейные подстановки с целыми коэффициентами. «Можно предположить, — пишет он далее, — что изучение аналогичных групп преобразований окажет большие услуги Арифметике. Это меня и побудило опубликовать следующие соображения, хотя они составляют скорее программу изучения, чем настоящую теорию» 21).
Пуанкаре начал искать, каким способом можно связать между собой и систематизировать проблемы диофантова анализа. Для этого он решил провести новую классификацию многочленов от двух переменных с целыми рациональными коэффициентами. За основу такой классификации он выбрал совокупность бирациональных преобразований с рациональными коэффициентами. Выше мы говорили, что аналогичную классификацию вводил и Риман. Отличие состоит в том, что Риман рассматривал бирациональные преобразования с комплексными коэффициентами, а Пуанкаре — с рациональными, что и позволило ему подойти к изучению арифметических свойств кривых.
Итак, согласно Пуанкаре две кривые эквивалентны или принадлежат одному классу, если от одной из них к другой можно перейти путём бирационального преобразования с рациональными коэффициентами 22). Так, например, любые две прямые коэффициенты которых рациональны, эквивалентны.
Чтобы показать это, Пуанкаре выбирает фиксированную рациональную После этого он переходит к коническим сечениям, Затем Пуанкаре рассматривает кубические кривые 2 то отсюда получаем d = 1, Однако доказательства необходимости у Эйлера не было. Достаточность наличия двойной точки для того, чтобы кубика 23) была эквивалентна рациональной прямой, Пуанкаре доказывает тем же способом, что и Эйлер, только проводит доказательство не аналитически, а геометрически. Он берёт эту двойную После этого Пуанкаре доказывает основную теорему, которая полностью решает вопрос о Теорема. Всякая кривая Следовательно, всякая кривая Отсюда, в частности, следует, что на всякой кривой Вопрос же о рациональных точках кривых Заметим, что аналогичные результаты, относящиеся к кривым Эти исследования Пуанкаре начинает с рассмотрения простейших кривых Предположим, что оно уже задано в таком виде. Пуанкаре излагает методы касательной и секущей Диофанта (разумеется, не упоминая имени последнего) для нахождения новых рациональных точек лежат на одной прямой. Пуанкаре уточняет и смысл этого равенства.
Дело в том, что интеграл
y где y определяется из уравнения (*), является бесконечнозначной функцией своего верхнего предела. Он несколько напоминает функцию
√1 – x² которая имеет свои «главные значения» в промежутке Подобно этому и
√x³ + ax + b имеет «главные значения», от которых все остальные отличаются на слагаемые вида Пуанкаре явно определяет сложение рациональных точек на эллиптической также принадлежит M.
Пуанкаре ставит вопрос: можно ли выбрать точки В переводе на язык теории групп это означает: имеет ли группа рациональных точек Пуанкаре называет точки Наименьшее число рациональных Можно показать, что ранг является инвариантом при бирациональных преобразованиях, Относительно ранга Пуанкаре ставит следующий вопрос: «Какие значения может принимать целое число, которое мы назвали рангом рациональной кубики?».
Этот вопрос был воспринят последующими математиками как утверждение, что ранг эллиптической кривой всегда конечен, После рассмотрения кубик Пуанкаре переходит к другим кривым Пусть f (x, y) = 0 — кривая Этим полностью решается вопрос о кривых Мемуар Пуанкаре содержит ещё и другие интересные идеи и «программы изучения», однако мы не можем здесь на них останавливаться. Отметим только один факт, интересный с точки зрения истории математики: Пуанкаре, Остановимся теперь на некоторых обобщениях, результатах и гипотезах, относящихся к арифметике алгебраических кривых.
Одно из обобщений было намечено уже в мемуаре Пуанкаре. От Диофанта и до Пуанкаре арифметические свойства кривых рассматривали над полем рациональных чисел, кривой Γ, всех бирациональных преобразований и координаты искомых точек должны были принадлежать полю рациональных чисел Q. Пуанкаре предложил провести подобные рассмотрения над полями алгебраических чисел, например, над квадратичным Но можно строить арифметику кривых и над совершенно произвольным В 1929 году французский математик Андре Вейль при помощи метода спуска Ферма доказал гипотезу Пуанкаре о конечности ранга эллиптической кривой над произвольным полем k.
Другое обобщение, начатое также Пуанкаре, относится к арифметике алгебраических кривых Параллельно с этим рассматривался вопрос о целых точках имеет только конечное число целых рациональных решений. Наиболее общий результат тут был получен немецким математиком К. Л. Зигелем, который, применив методы А. Туэ и методы Морделла–Вейля, показал, что число целых точек кривой над полем k алгебраических чисел, если род Что касается рациональных точек на кривой Отметим, что все теоремы, доказанные относительно системы образующих группы рациональных точек эллиптической кривой, являются чистыми теоремами существования: неизвестно никакого эффективного приёма для нахождения образующих. Остаётся открытым вопрос Пуанкаре о том, какие значения может принимать число, которое он назвал рангом эллиптической кривой. До сих пор неизвестно, существуют ли кривые, ранг которых был бы больше 11, но и не доказано, что ранг не может принимать сколь угодно больших значений. Единственный результат здесь получен советским математиком А. И. Лапиным, который доказал, что над полем рациональных функций существуют кривые сколь угодно большого ранга.
Глубокие результаты, относящиеся к установлению существования рациональных точек на эллиптической кривой, принадлежат советскому математику И. Р. Шафаревичу и американскому математику Дж. Тэйту. Однако здесь мы не можем привести не только доказательства, но и формулировки результатов, так как для этого требуются более обширные сведения из современной алгебры и алгебраической геометрии, чем мы имеем право предполагать в этой брошюре. К тому же мы от истории вопроса перешли к современности и читатель сможет, если захочет, более подробно познакомиться с нынешним состоянием диофантовых уравнений по обзорным статьям. Укажем, например, на статью Дж. Касселса «Диофантовы уравнения со специальным рассмотрением эллиптических кривых», опубликованную в журнале «Математика» (№ 1 и № 2 за 1968 год). I. Издания сочинений Диофанта. Общепринятый теперь текст «Арифметики» Диофанта и его небольшого трактата «О многоугольных числах» был издан в 1893 году (вместе с переводом на латинский язык) известным французским историком науки Полем Таннери. Во втором томе издания собраны все греческие комментарии к сочинениям Диофанта. Приведём название и выходные данные этого издания:
С издания Таннери сделаны следующие переводы:
Приведу ещё фрагмент вступительной статьи И. Г. Башмаковой из этой книги:
Здесь уместно поставить вопрос о том, каковы были познания самого Диофанта в теории чисел. Для ответа на него соберём вместе все предложения по теории чисел, которые Диофант формулирует явно или на которые он опирается в своей «Арифметике».
Из приведённой сводки видно, что Диофантом был хорошо изучен вопрос о представлении чисел формой Попытаемся в заключение представить себе, каковы же были сведения Диофанта в тех вопросах, которые мы теперь относим к алгебраической геометрии.
Сама последовательность книг показывает, что Диофант классифицировал задачи по степеням уравнений, к которым они сводятся. Так, в первых трёх книгах помещены задачи, которые сводятся либо к уравнению не выше второй степени, либо к «двойному уравнению», каждое из которых имеет Но, помимо степеней, Диофант различал уравнения и по другому, более глубокому признаку, а именно по тому, униформизируются ли они в рациональных функциях. Мы говорили уже выше, что эта проблема была полностью им решена для уравнения второй степени от двух переменных. Далее, Диофант знал, что для некоторых уравнений третьей и четвёртой степени такая униформизация также возможна, а для других нет. Уравнения, определяющие кривые у которой существуют рациональные точки Наконец, следует отметить, что при всех своих решениях Диофант всегда принимал во внимание случаи, соответствующие наличию бесконечно удалённых рациональных точек кривых или поверхностей (разумеется, не вводя этого понятия).
— E.G.A. II. Литература о Диофанте очень бедна. О нём можно прочитать в общих курсах истории математики, например,
а также в книге
и в статье
III. Литература о диофантовых уравнениях и алгебраической геометрии.
![]() и, таким образом, получил возможность обозначать первые шесть отрицательных степеней неизвестного. Например,
и, таким образом, получил возможность обозначать первые шесть отрицательных степеней неизвестного. Например, ![]() ,
,![]() .
.
° ° Δυ̃ σβ Μ ιγ ![]()
ς ι ΐσ Μ ιγ 5).
ì í î
f1(x1, x2, ... , xn) = 0, · · · · · · · · · · fm(x1, x2, ... , xn) = 0 (1)
f (x, y) = 0.
(2)

Рис. 1.
k = –
fx' (x0, y0)
.
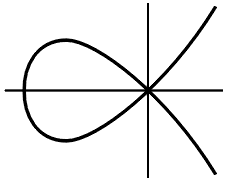
Рис. 2.
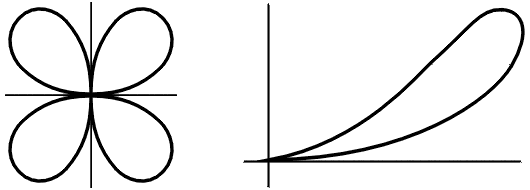
Рис. 3.
f (x, y) = 0
(*)
p =
(n – 1)(n – 2)
– d.
x = φ(u, v), y = ψ(u, v),
(3)
G(u, v) = 0.
(4)
u = φ1(x, y), v = ψ1(x, y),
(3')
ì í î
x = φ(u, v) = au + bv + c,
y = ψ(u, v) = a1u + b1v + c1, причём
a
a1 b
b1 ≠ 0,
y2 = x4 – x3 + 2x – 2 = (x – 1)(x3 + 2).
(*)
x – 1 =
1
,
y
= v.
x =
1 + u
, y =
v
u =
1
, v =
y
,
v =
y
.
y2 = x3 + ax + b,
(5)
x2 + y2 = a2,
(6)
ì í î
x = x,
y = kx – a.(7)
y = kx – a.
(7')
x =
2ak
, y = kx – a = a
k2 – 1
.
f2(x, y) = 0
(8)
ì í î
x = a + t,
y = b + kt
t = –
A(a, b) + kB(a, b)
.
y2 = a2x2 + bx + c,
(9)
x =
c – m2
.
x =
u
, y =
v
.
v2 = a2u2 + buz + cz2.
(9')
∫
dx
f3(x, y) = 0
(10)
x(a – x) = y3 – y.
(11)
y = kx – 1
(*)
2k = a, т.е. k = a/2,
(**)
x =
3k2 – 1
= 2·
3a2 – 4
.
y – b = k(x – a)
(12)
ì í î
x = a + t,
y = b + kt.(13)
A(a, b) + kB(a, b) = 0,
(14)
k = –
A(a, b)
= –
∂f3 ∂f3 (P),
dy
= –
∂f3 ∂f3 .
a3x3 + x2 – a3x – 1 = y3.
(15)
x =
a3 + 3a
.
a3u3 + u2z – a3uz2 – z3 = v3.
(15')
ì í î
x + y = 1, x + a = u2, y + a = v2.
x3 + y3 = a3 – b3,
(*)
t =
3a3b
.
f (x, y) = 0
(*)
x =
u
, y =
v
;
Φ(u, v, z) = 0.
(**)
y2 = ax2 + bx + c
(16)
y2 = ax3 + bx2 + cx + d
(17)
x =
k2 + aβ
, y = k
k2 + aβ – aα
.
ì í î
y2 = ax3 + bx2 + cx + d, 3ax2 + 2bx + c = 0, 2y = 0,
F3(α) = f 2, F3(β) = g2;
(18)
y = f +
g – f
(x – α) или y = g +
f – g
(x – β),
F3(x) =
f +
g – f
(x – α)
2
.
y2 = x3 + ax + b 16)
(19)
x
Π(A) =
∫
dx
.
∞
Π(A) + Π(B) = Π(C).
(20)
Π(D) = nΠ(A),
(21)
Π(D) = 2Π(A).
(22)
x
x
Π(A') =
∫
dx
= –
∫
dx
= –Π(A).
∞
∞
x =
u
, y =
v
,
v2z = u3 + auz2 + bz3.
(19')
∞
Π(O) =
∫
dx
= 0.
∞
y2 = ax4 + bx3 + cx2 + dx + e,
(*)
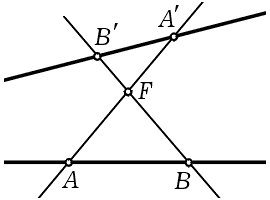
Рис. 4.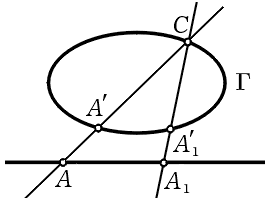
Рис. 5.
0 =
(3 – 1)(3 – 2)
– d,
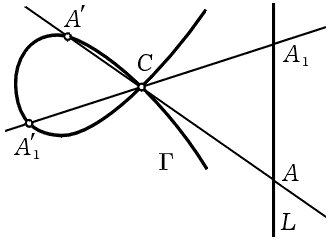
Рис. 6.
y2 = x3 + ax + b.
(*)
Π(A) + Π(B) + Π(C) = 0,
(**)
u
∫
dx
,
a
u
∫
dx
= arcsin u,
0
u
∫
dx
0
A = m1A1 + ... + msAs
(***)
Diophante d'Alexandrie, Les six livres arithmétiques et le livre des nombres polygones, trad. par Paul Ver Eecke. Bruges, 1926 (переизд. Paris, 1959).
Diophantus Alexandrinus, Arithmetik des Diophantos aus Alexandria, Aus dem Griech. übertr. and erklärt
Heath Th. L., Diophantus of Alexandria, A Study in the History of Greek Algebra. Cambridge, 1910 (эта книга была переиздана в
Диофант Александрийский. Арифметика и книга о многоугольных числах (перевод с древнегреческого И. Н. Веселовского; редакция и комментарии И. Г. Башмаковой). М., «Наука», 1974.
| x = | 16 a3 – 1 |
, y = ax = | 16a a3 – 1 |
. |
где P — некоторая точка конечного порядка. назад к тексту
 Сведения об авторе
Сведения об авторе
Башмакова Изабелла Григорьевна родилась 3 января 1921 г. в Ростове-на-Дону. В 1938 г. поступила на мехмат МГУ. Во время Отечественной войны находилась в эвакуации и работала медсестрой в Самарканде. По возвращении в Москву в 1943 г. познакомилась с С. А. Яновской и стала её любимой ученицей, а затем и сотрудницей. Первые доклады сделала на семинаре по истории математики в МГУ, которым в то время руководили С. А. Яновская и А. П. Юшкевич. Вся дальнейшая работа Изабеллы Григорьевны связана с МГУ, где она работает и поныне профессором истории математики. По окончании аспирантуры И. Г. Башмакова защитила кандидатскую диссертацию «Из истории теории делимости». В 1961 г. защитила в качестве докторской диссертации совокупность своих исследований по античной математике. В 1968 г. ей было присвоено звание профессора. В 1966 г. Международная Академия истории науки избрала её членом-корреспондентом (в 1971 г. — академиком). Среди её исследований по античной математике первых веков нашей эры, особенно существенны работы по истории диофантова анализа. УМН, 1981, т. 36, № 5, с.211–213. |