Why are special functions special?

Michael Berry

According to legend, Leo Szilard's baths were ruined by his conversion to biology. He had enjoyed soaking for hours while thinking about physics. But as a convert he found this pleasure punctuated by the frequent need to leap out and search for a fact. In physics—particularly theoretical physics—we can get by with a few basic principles without knowing many facts; that is why the subject attracts those of us cursed with poor memory.

But there is a corpus of mathematical information that we do need. Much of this consists of formulas for the "special" functions. How many of us remember the expansion of cos 5x in terms of cos x and sin x, or whether an integral obtained in the course of a calculation can be identified as one of the many representations of a Bessel function, or whether the asymptotic expression for the gamma function involves (n + ½) or (n – ½)? For such knowledge, we theorists have traditionally relied on compilations of formulas. When I started research, my peers were using Jahnke and Emde's Tables of Functions with Formulae and Curves (J&E)¹ or Erdélyi and coauthors' Higher Transcendental Functions.²

Then in 1964 came Abramowitz and Stegun's Handbook of Mathematical Functions (A&S),³ perhaps the most successful work of mathematical reference ever published. It has been on the desk of every theoretical physicist. Over the years, I have worn out three copies. Several years ago, I was invited to contemplate being marooned on the proverbial desert island. What book would I most wish to have there, in addition to the Bible and the complete works of Shakespeare? My immediate answer was: A&S. If I could substitute for the Bible, I would choose Gradsteyn and Ryzhik's Table of Integrals, Series and Products.⁴ Compounding the impiety, I would give up Shakespeare in favor of Prudnikov, Brychkov and Marichev's Integrals and Series.⁵ On the island, there would be much time to think about physics and much physics to think about: waves on the water that carve ridges on the sand beneath and focus sunlight there; shapes of clouds; subtle tints in the sky... With the arrogance that keeps us theorists going, I harbor the delusion that it would be not too difficult to guess the underlying physics and formulate the governing equations. It is when contemplating how to solve these equations—to convert formulations into explanations—that humility sets in. Then, compendia of formulas become indispensable.

Nowadays the emphasis is shifting away from books towards computers. With a few keystrokes, the expansion of cos 5x, the numerical values of Bessel functions, and many analytical integrals can all be obtained easily using software such as Mathematica and Maple. (In the spirit of the times, I must be even handed and refer to both the competing religions.) A variety of resources is available online. The most ambitious initiative in this direction is being prepared by NIST, the descendant of tho US National Bureau of Standards, which published A&S. NIST's forthcoming Digital Library of Mathematical Functions (DLMF) will be a free Web-based collection of formulas (http://dlmf.nist.gov), cross-linked and with live graphics that can be magnified and rotated. (Stripped-down versions of the project will be issued as a book and a CD-ROM for people who prefer those media.)

The DLMF will reflect a substantial increase in our knowledge of special functions since 1964, and will also include new families of functions. Some of these functions were (with one class of exceptions) known to mathematicians in 1964, but they were not well known to scientists, and had rarely been applied in physics. They are new in the sense that, in the years since 1964, they have been found useful in several branches of physics. For example, string theory and quantum chaology now make use of automorphic functions and zeta functions; in the theory of solitons and integrable dynamical systems, Painlevé transcendents are widely employed; and in optics and quantum mechanics, a central role is played by "diffraction catastrophe" integrals, generated by the polynomials of singularity theory—my own favorite, and the subject of a chapter I am writing with Christopher Howls for the DLMF.

Kelvin's ship-wave pattern, calculated with the Airy function, the simplest special function in the hierarchy of diffraction catastrophes.

This continuing and indeed increasing reliance on special functions is a surprising development in the sociology of our profession. One of the principal applications of these functions was in the compact expression of approximations to physical problems for which explicit analytical solutions could not be found. But since the 1960s, when scientific computing became widespread, direct and "exact" numerical solution of the equations of physics has become available in many cases. It was often claimed that this would make the special functions redundant. Similar skepticism came from some pure mathematicians, whose ignorance about special functions, and lack of interest in them, was almost total. I remember that when singularity theory was being applied to optics in the 1970s, and I was seeking a graduate student to pursue these investigations, a mathematician recommended somebody as being very bright, very knowledgeable, and interested in applications. But this student had never heard of Bessel functions (nor could he carry out the simplest integrations, but that is another story).

A cross section of the elliptic umbilic, a member of the hierarchy of diffraction catastrophes.

The persistence of special functions is puzzling as well as surprising. What are they, other than just names for mathematical objects that are useful only in situations of contrived simplicity? Why are we so pleased when a complicated calculation "comes out" as a Bessel function, or a Laguerre polynomial? What determines which functions are "special"? These are slippery and subtle questions to which I do not have clear answers. Instead, I offer the following observations.

There are mathematical theories in which some classes of special functions appear naturally. A familiar classification is by increasing complexity, starting with polynomials and algebraic functions and progressing through the "elementary" or "lower" transcendental functions (logarithms, exponentials, sines and cosines, and so on) to the "higher" transcendental functions (Bessel, parabolic cylinder, and so on). Functions of hypergeometric type can be ordered by the behavior of singular points of the differential equations representing them, or by a group-theoretical analysis of their symmetries. But all these classifications are incomplete, in the sense of omitting whole classes that we find useful. For example, Mathieu functions fall outside the hypergeometric class, and gamma and zeta functions are not the solutions of simple differential equations. Moreover, even when the classifications do apply, the connections they provide often appear remote and unhelpful in our applications.

One reason for the continuing popularity of special functions could be that they enshrine sets of recognizable and communicable patterns and so constitute a common currency. Compilations like A&S and the DLMF assist the process of standardization, much as a dictionary enshrines the words in common use at a given time. Formal grammar, while interesting for its own sake, is rarely useful to those who use natural language to communicate. Arguing by analogy, I wonder if that is why the formal classifications of special functions have not proved very useful in applications.

The cusp, a member of the hierarchy of diffraction catastrophes.

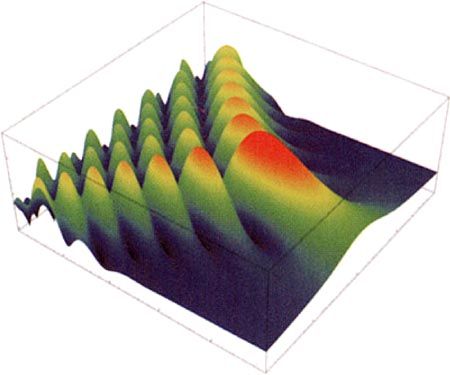
Sometimes the patterns embodying special functions are conjured up in the form of pictures. I wonder how useful sines and cosines would be without the images, which we all share, of how they oscillate. In 1960, the publication in J&E of a 3D graph showing the poles of the gamma function in the complex plane acquired an almost iconic status. With the more sophisticated graphics available now, the far more complicated behavior of functions of several variables can be explored in a variety of 2D sections and 3D plots, generating a large class of new and shared insights.

"New" is important here. Just as new words come into the language, so the set of special functions increases. The increase is driven by more sophisticated applications, and by new technology that enables more functions to be depicted in forms that can be readily assimilated.

Sometimes the patterns are associated with the asymptotic behavior of the functions, or of their singularities. Of the two Airy functions, Ai is the one that decays towards infinity, while Bi grows; the J  Bessel functions are regular at the origin, the Y  Bessel functions have a pole or a branch point.

Perhaps standardization is simply a matter of establishing uniformity of definition and notation. Although simple, this is far from trivial. To emphasize the importance of notation, Robert Dingle in his graduate lectures in theoretical physics at the University of St. Andrews in Scotland would occasionally replace the letters representing variables by nameless invented squiggles, thereby inducing instant incomprehensibility. Extending this one level higher, to the names of functions, just imagine how much confusion the physicist John Doe would cause if he insisted on replacing sin x by doe x), even with a definition helpfully provided at the start of each paper.

To paraphrase an aphorism attributed to the biochemist Albert Szent-Györgyi, perhaps special functions provide an economical and shared culture analogous to books: places to keep our knowledge in, so that we can use our heads for better things.

Singular Limits

Michael Berry

Biting into an apple and finding a maggot is unpleasant enough, but finding half a maggot is worse. Discovering one-third of a maggot would be more distressing still: The less you find, the more you might have eaten. Extrapolating to the limit, an encounter with no maggot at all should be the ultimate bad-apple experience. This remorseless logic fails, however, because the limit is singular: A very small maggot fraction ( f <<1) is qualitatively different from no maggot ( f = 0). Limits in physics can be singular too—indeed they usually are—reflecting deep aspects of our scientific description of the world.

In physics, limits abound and are fundamental in the passage between descriptions of nature at different levels. The classical world is the limit of the quantum world when Planck's constant h is inappreciable; geometrical optics is the limit of wave optics when the wavelength λ is insignificant; thermodynamics is the limit of statistical mechanics when the number of particles N is so large that 1/N is negligible; mechanics of a slippery fluid is the limit of mechanics of a viscous fluid when the inverse Reynolds number 1/R can be disregarded. These limits have a common feature: They are all singular—they must be, because the theories they connect involve concepts that are qualitatively very different. As I explain here, there are both reassuring and creative aspects to singular limits. And by regarding them as a general feature of physical science, we get insight into two related philosophical problems: how a more general theory can reduce to a less general theory and how higher-level phenomena can emerge from lower-level ones.

The coherence of our physical worldview requires the reassurance that, singularities notwithstanding, quantum mechanics does reduce to classical mechanics, statistical mechanics does reduce to thermodynamics, and so on, in the appropriate limits. We know that when calculating the orbit of a spacecraft (and indeed knowing that it has an orbit) we can safely use classical mechanics, rather than having to solve the Schrödinger equation. An engineer designing a bridge can rely on continuum elasticity theory, without needing to know the atomic arrangements underlying the equation of state of the materials used in the construction. However, getting these reassurances from fundamental theory can involve subtle and unexpected concepts.

Perhaps the simplest example is two flashlights shining on a wall. Their combined light is twice as bright as when each shines separately: This is the optical embodiment of the equation 1+1=2. But we learned from Thomas Young almost exactly two centuries ago that this mathematics does not describe the intensity of superposed light beams: To account for wave interference, amplitudes must be added, and the sum then squared to give the intensity. This involves the phases of the two waves, ±φ say, and gives the intensity as |exp(iφ) + exp(–iφ)|² = 2 + 2cos 2φ, which can take any value between 0 and 4. So, what becomes of 1+1=2? Young himself, responding to a critic who claimed that the wall should be covered with interference fringes, agreed, but pointed out that ''the fringes will demonstrably be invisible ... a hundred ... would not cover the point of a needle." Underlying this explanation is a singular limit: The unwanted cos 2φ does not vanish but oscillates rapidly. If the beams make an angle θ the fringe spacing is λ/2θ, vanishing in the geometrical limit of small λ. The limit is singular because the cosine oscillates infinitely fast as λ vanishes. Mathematically, this is an essential singularity of a type dismissed as pathological to students learning mathematics, yet here it appears naturally in the geometrical limit of the simplest wave pattern.

Young's "demonstrable" invisibility requires an additional concept, later made precise by Augustin Jean Fresnel and Lord Rayleigh: The rapidly varying cos 2φ must be replaced by its average value, namely zero, reflecting the finite resolution of the detectors, the fact that the light beam is not monochromatic, and the rapid phase variations in the uncoordinated light from the two flashlights. Only then does 1+1=2 apply—a relation thus reinterpreted as a singular limit.

Nowadays this application of the idea that the average of a cosine is zero, elaborated and reincarnated, is called decoherence. This might seem a bombastic redescription of the commonplace, but the applications of decoherence are far from trivial. Decoherence quantifies the uncontrolled extraneous influences that could upset the delicate superpositions in quantum computers. And, as we have learned from the work of Wojciech Zurek and others, the same concept governs the emergence of the classical from the quantum world in situations more sophisticated than Young's, where chaos is involved. For example, the chaotic tumbling of Saturn's satellite Hyperion, regarded as a quantum rotator with about 10⁶⁰ quanta of angular momentum, would, according to an unpublished calculation by Ronald Fox, be suppressed in a few decades by the discrete nature of the energy spectrum. However, nobody expects to witness this suppression, because Hyperion is not isolated: Just one photon arriving from the Sun (whose reemission enables our observations) destroys the coherence responsible for quantization in a time of the order of 10^–50 seconds, and reinstates classicality.¹ Alternatively stated, decoherence suppresses the quantum suppression of chaos.

Other reassurances are equally hard to come by. For example, formally obtaining thermodynamics from statistical mechanics involves applying the mathematical saddle-point method to an infinite-dimensional integral. But although such reassurances about the appropriate application of earlier, less general theories are welcome, they look backward rather than forward. However, there is a creative side to singular limits: They lead to new physics. For large N, where a central idea is symmetry-breaking, this creative side is concisely expressed in Philip Anderson's celebrated phrase: More is different.² The vast literature on critical phenomena reflects the fact that the large-N limit of statistical mechanics is singular at a critical point because there the continuum postulated in the thermodynamic limit is never reached, even when averaging over distances far exceeding the spacing between atoms. Correlations span arbitrarily large distances, and the critical state—the new physics—is a fractal. The zero-viscosity limit of fluid mechanics is singular because of the still-mysterious phenomenon of turbulence, whose definitive understanding would earn one of the Clay Foundation's $1 million prizes.

In quantum mechanics (and indeed the physics of waves of all kinds), a range of new phenomena lurk in the borderland with classical mechanics. High-lying energy levels display remarkable universality: Their statistics depend only on whether the corresponding classical orbits are regular or chaotic, and on certain global symmetries. In the chaotic case (see the column "Quantum Chaos and the Bow-Stern Enigma" by Daniel Kleppner, Physics Today, August 1991, page 9), the associated wavefunctions resemble random functions of position decorated by "scars" along classical periodic orbits. (See the article "Postmodern Quantum Mechanics," by Eric J. Heller and Steven Tomsovic, Physics Today, July 1993, page 38.) For regular motion, the dominant feature is focusing, and the classical paths are singular on caustics; the caustics are decorated with striking and characteristic interference patterns (see my column "Why Are Special Functions Special?" in Physics Today, April 2001, page 11). Such postmodern quantum effects are emergent phenomena par excellence: The discrete states they describe are essentially nonclassical, but can be unambiguously identified only for highly excited states, that is, under near-classical conditions.

a     b

Across the boundary between classically allowed and forbidden regions in a 2D chaotic system, the density of trajectories falls discontinuously to zero. This classical limit is singular because, in the corresponding semiclassical quantum wavefunctions shown here as simulations (with the classical boundary indicated by dashed lines), (a) the probability density (color-coded from red at maxima to black at zeros) fluctuates smoothly, and (b) the phase (color-coded by hue) varies smoothly except at points where all colors meet (points that are themselves singularities).

New ideas in physics often inspire, or are inspired by, new ideas in mathematics, and singular limits are no exception. Underlying critical phenomena is the renormalization group, which determines how systems transform, or remain invariant, under changes of scale—a fertile idea that is essentially mathematical but whose foundations have not been rigorously established. The quantum-classical connection involves divergent infinite series (for example, in powers of h), and the divergence can be traced precisely to the singularity of the limit. Some quantum phenomena involving divergent series are nonclassical reflection above a smooth potential barrier, weak quantum transitions caused by slowly varying external forces, and the representation of spectra in terms of classical periodic orbits. Mathematicians long regarded divergent series with suspicion; in 1828, Niels Henrik Abel wrote that they "are an invention of the devil, and it is shameful to base on them any demonstration whatsoever." But such series are often the best (even the only) way to calculate physical quantities, and applied mathematicians, disregarding Abel's censure, have freely developed sophisticated manipulations and regularizations of the divergences. An elementary example of a divergent series is 1+2+3+4+..., which can be resummed to give the value –1/12; this looks like a joke, but is the unambiguous result of zeta function regularization, widely used in quantum field theory. Much more violent divergences arise from singular limits associated with the integrals and differential equations of physics, and have been tamed using more sophisticated methods. This is the domain of mathematical asymptotics and singular perturbation theory. In the 1990s, the long overdue beginnings of a rigorous mathematical theory were established.

Singular limits carry a clear message, which philosophers are beginning to hear:³ The physics of singular limits is the natural philosophy of renormalization and divergent series. Perhaps they are recognizing that some problems of theory reduction can themselves be reduced to tricky questions in mathematical asymptotics an extension of the traditional philosophical method, of argumentation based on words. Usually, we think of "applications" of science going from the more general to the more specific—physics to widgets—but this is an application that goes the other way: from physics to philosophy. One wonders if it counts with those journalists or administrators who like to question whether our research has applications. Probably not.