| В МИРЕ НАУКИ Scientific American · Издание на русском языке № 2 · ФЕВРАЛЬ 1987 · С. 16–28 |
Хаос
| В МИРЕ НАУКИ Scientific American · Издание на русском языке № 2 · ФЕВРАЛЬ 1987 · С. 16–28 |
Огромная сила науки заключена в её способности устанавливать связь между причиной и следствием. Например, законы гравитации позволяют предсказывать затмения на тысячи лет вперёд. Другие явления природы не поддаются столь точному предсказанию. Течения в атмосфере так же строго подчиняются физическим законам, как и движения планет, тем не менее прогнозы погоды всё ещё имеют вероятностный характер. И погода, и течение горной реки, и движение брошенной игральной кости имеют в своём поведении непредсказуемые аспекты. Так как в этих явлениях не видно чёткой связи между причиной и следствием, говорят, что в них присутствует элемент случайности. Однако до недавнего времени было мало оснований сомневаться в том, что в принципе можно достичь точной предсказуемости. Считалось, что для этого необходимо только собрать и обработать достаточное количество информации.
Такую точку зрения круто изменило поразительное открытие: простые детерминированные системы с малым числом компонент могут порождать случайное поведение, причём эта случайность имеет принципиальный характер — от неё нельзя избавиться, собирая больше информации. Порождаемую таким способом случайность стали называть хаосом.
Кажущийся парадокс состоит в том, что хаос детерминирован — порождён определёнными правилами, которые сами по себе не включают никаких элементов случайности. В принципе будущее полностью определено прошлым, однако на практике малые неопределённости растут и поэтому поведение, допускающее краткосрочный прогноз, на долгий срок непредсказуемо. Таким образом, в хаосе есть порядок: в основе хаотического поведения лежат изящные геометрические структуры, которые создают случайность таким же способом, как создает её сдающий карты, тасуя колоду, или миксер, размешивая тесто для бисквита.
 0 |
 1 |
 2 |
 3 |
 4 |
 5 |
 7 |
 10 |
 18 |
 47 |
 48 |
 237 |
 239 |
 240 |
 241 |
Рис. 1. Хаос связан с применением геометрической операции растяжения. Эффект растяжения проиллюстрирован на примере портрета французского математика Анри Пуанкаре, основоположника теории динамических систем. Исходное изображение (вверху слева) было преобразовано в цифровую форму, так чтобы операцию растяжения мог выполнять компьютер. Простое математическое преобразование растягивает изображение по диагонали, как будто оно нарисовано на резиновой поверхности. Там, где изображение вылезает за рамки исходного, оно обрезается и вставляется с другой стороны, как показано на кадре 1. (Номер кадра указывает на количество выполненных преобразований.) После повторных применений преобразования разобрать лицо уже невозможно |
Открытие хаоса породило новый образец научного моделирования. С одной стороны, оно ввело новые принципиальные ограничения на возможность предсказаний. С другой стороны, заложенный в хаосе детерминизм показал, что многие случайные явления более предсказуемы, чем считалось раньше. Собранная в прошлом информация, казавшаяся случайной и отправленная на полку как слишком сложная, теперь получила объяснение при помощи простых законов. Хаос позволяет находить порядок в столь различных системах, как атмосфера, подтекающий водопроводный кран или сердце. Это революционное открытие затронуло многие области науки.
Каковы источники случайного поведения? Классическим примером служит броуновское движение. Рассматриваемая в микроскоп пылинка совершает свой безостановочный и беспорядочный танец под действием теплового движения окружающих её молекул воды. Поскольку молекулы воды невидимы, а число их огромно, точное движение пылинки совершенно непредсказуемо. Таким образом, паутина причинных воздействий одних частей системы на другие может стать настолько запутанной, что окончательная картина поведения будет совсем случайной.
Хаос, о котором речь пойдёт в статье, не связан ни с большим числом компонент, ни с их невидимыми воздействиями. Наличие случайного поведения в очень простых системах заставляет
Почему предвидеть течения в атмосфере намного труднее, чем движения в Солнечной системе? И та, и другая составлены из многих частей, и обе подчиняются второму закону Ньютона
|
Лаплас, 1776 год «Состояние системы природы в настоящем есть, очевидно, следствие того, каким оно было в предыдущий момент, и если мы представим себе разум, который в данное мгновение постиг все связи между объектами Вселенной, то он сможет установить соответствующие положения, движения и общие воздействия всех этих объектов в любое время в прошлом или в будущем. Физическая астрономия, область знания, которая делает величайшую честь человеческому уму, даёт нам представление, хотя и неполное, чем был бы такой разум. Простота законов, по которым движутся небесные тела, и соотношения между их массами и расстояниями позволяют проанализировать их движение до определённой точки, и, чтобы определить состояние системы этих крупных тел в прошлых или будущих веках, математику достаточно того, чтобы их положение и скорость были получены из наблюдений в любой момент времени. Человек обязан этим мощности приборов, которыми он пользуется, и небольшому числу соотношений, которые он применяет в своих расчётах. Однако незнание различных причин, вызывающих те или иные события, а также их сложность в сочетании с несовершенством анализа мешает нам достичь той же уверенности по отношению к огромному большинству явлений. Таким образом, существуют вещи, которые для нас неопределённы, вещи, более или менее вероятные, и мы стараемся компенсировать невозможность их узнать, определяя различные степени их достоверности. Получается, что слабости человеческого разума мы обязаны появлением одной из самых тонких и искусных математических теорий — науки о случае, или о вероятности». Пуанкаре, 1903 год «Совсем незначительная причина, ускользнувшая от нашего внимания, вызывает значительный эффект, который мы не можем не заметить, и тогда мы говорим, что этот эффект вызван случаем. Если бы мы точно знали законы природы и положение Вселенной в начальный момент, мы могли бы точно предсказать положение той же Вселенной в последующий момент. Но даже если бы законы природы открыли нам все свои тайны, мы и тогда могли бы знать начальное положение только приближённо. Если бы это позволило нам предсказать последующее положение с тем же приближением, это было бы всё, что нам требуется, и мы могли бы сказать, что явление было предсказано, что оно управляется законами. Но это не всегда так; может случиться, что малые различия в начальных условиях вызовут очень большие различия в конечном явлении. Малая ошибка в первых породит огромную ошибку в последнем. Предсказание становится невозможным, и мы имеем дело с явлением, которое развивается по воле случая». |
Взгляды двух великих учёных на случайность и вероятность совершенно противоположны. Французский математик Пьер Симон Лаплас полагал, что законы природы подразумевают строгий детерминизм и полную предсказуемость, хотя несовершенство наблюдений и требует введения теории вероятностей. Высказывание Пуанкаре предвосхищает современный взгляд, согласно которому сколь угодно малые неопределённости в состоянии системы могут усиливаться со временем и предсказания отдалённого будущего могут стать невозможными. |
Наука XX века покончила с лапласовым детерминизмом. Первый удар ему нанесла квантовая механика. Одно из главных положений этой теории — открытый Гейзенбергом принцип неопределённости, который утверждает, что одновременно положение и скорость частицы не могут быть точно измерены. Принцип неопределённости хорошо объясняет, почему некоторые случайные явления, такие, как радиоактивный распад, не подчиняются лапласову детерминизму. Ядро настолько мало, что вступает в силу принцип неопределённости, и точно знать происходящие в ядре процессы принципиально невозможно, а потому, сколько бы ни было собрано о нём информации, нельзя точно предсказать, когда оно распадётся.
Однако источник непредсказуемости для крупномасштабных систем следует искать в другом. Одни крупномасштабные явления предсказуемы, другие — нет, и квантовая механика тут ни при чём. Например, траектория бейсбольного мяча в принципе предсказуема, и каждый игрок интуитивно пользуется этим всякий раз, когда ловит мяч. Напротив, траектория воздушного шара, когда из него вырывается воздух, непредсказуема: он кренится и беспорядочно вертится в
Классический пример подобного двоякого поведения даёт течение жидкости. При одних обстоятельствах оно является ламинарным — ровным, устойчивым, регулярным — и легко предсказывается при помощи уравнений. При других обстоятельствах течение становится турбулентным — неровным, неустойчивым, нерегулярным — и трудно предсказуемым. Переход от ламинарного поведения к турбулентному знаком каждому, кто хоть раз летел в самолёте в спокойную погоду и затем внезапно попадал в грозу. Чем объяснить существенную разницу между ламинарным и турбулентным течением?
Чтобы лучше понять, в чём тут загадка, допустим, что мы решили посидеть у горного ручья. Вода кружится в водоворотах и плещется так, будто по собственной воле бросается то туда, то сюда. Но ведь камни в русле ручья прочно лежат на месте, а приток воды почти одинаков. Чем же вызван случайный характер её движения?
Советский физик Л. Д. Ландау в своё время предложил объяснение случайного движения жидкости, которое господствовало много лет. Оно состояло в том, что в турбулентном течении возникает много различных независимых колебаний (вихрей). При увеличении скорости течение станет ещё более турбулентным и постепенно, по одной, будут прибавляться новые частоты. Хотя каждое отдельное колебание может быть простым, их сложное сочетание приводит к движению, которое невозможно предсказать.
Однако по поводу теории Ландау возникли сомнения. Случайное поведение проявляют даже системы, не отличающиеся ни особой сложностью, ни неопределённостью. Ещё на рубеже века это осознал французский математик Анри Пуанкаре, отметив, что непредсказуемые, возникающие «по воле случая» явления присущи скорее таким системам, где небольшие изменения в настоящем приводят к заметным изменениям в будущем. Представим себе камень на вершине холма.
Чтобы показать, насколько чутко реагируют некоторые физические системы на внешние воздействия, приведём простой пример. Представим себе несколько идеализированный бильярд, в котором шары катятся по столу и сталкиваются между собой так, что потерями энергии можно пренебречь. Игрок делает один удар, и начинается длинная серия столкновений; естественно, он хочет знать, что последует за его ударом. На какой срок может игрок, в совершенстве контролирующий свой удар, предсказать траекторию шара, который он толкнул своим кием? Если он пренебрежёт даже столь малым воздействием, как гравитационное притяжение электрона на краю галактики, прогноз окажется неверным уже через одну минуту!
Быстрый рост неопределённости объясняется тем, что шары не идеальны, и небольшие отклонения от идеальной траектории в точке удара с каждым новым столкновением увеличиваются. Рост происходит экспоненциально подобно тому, как размножаются бактерии в условиях неограниченного пространства и запаса пищи. С каждым новым столкновением ошибки накапливаются, и любое даже самое малое воздействие быстро достигает макроскопических размеров. Это одно из основных свойств хаоса1.
Экспоненциальное накопление ошибок, свойственное хаотической динамике, стало вторым камнем преткновения для лапласова детерминизма. Квантовая механика установила, что начальные измерения всегда неопределённы, а хаос гарантирует, что эти неопределённости быстро превысят пределы предсказуемости. Не будь хаоса, Лаплас мог бы тешиться надеждой, что ошибки останутся ограниченными или хотя бы будут расти достаточно медленно, позволяя делать долгосрочный прогноз. При наличии хаоса достоверность прогнозов быстро падает.
Понятие хаоса относится к так называемой теории динамических систем. Динамическая система состоит из двух частей: понятия состояния (существенной информации о системе) и динамики (правила, описывающего эволюцию системы во времени). Эволюцию можно наблюдать в пространстве состояний, или фазовом пространстве, — абстрактном пространстве, в котором координатами служат компоненты состояния. При этом координаты выбираются в зависимости от контекста. В случае механической системы это могут быть положение и скорость, в случае экологической модели — популяции различных биологических видов.
Хороший пример динамической системы — простой маятник. Его движение задаётся всего двумя переменными: положением и скоростью. Таким образом, его состояние — это точка на плоскости, координаты которой — положение маятника и его скорость. Эволюция состояния описывается правилом, которое выводится из законов Ньютона и выражается математически в виде дифференциального уравнения. Когда маятник качается
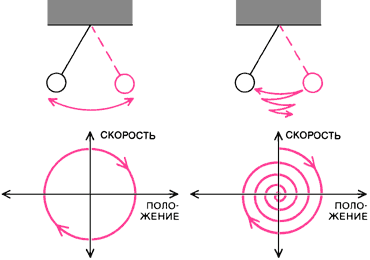 |
Рис. 2. Фазовое пространство даёт удобное средство для наглядного представления поведения динамической системы. Это абстрактное пространство, координатами в котором являются степени свободы системы. Например, движение маятника (вверху) полностью определено его начальной скоростью и положением. Таким образом, его состоянию отвечает точка на плоскости, координатами которой являются положение и скорость маятника (внизу). Когда маятник качается, эта точка описывает некоторую траекторию, или «орбиту», в фазовом пространстве. Для идеального маятника без трения орбита представляет собой замкнутую кривую (внизу слева), в противном случае орбита сходится по спирали к точке (внизу справа). |
Динамическая система может развиваться либо в непрерывном времени, либо в дискретном времени. Первая называется потоком, вторая — отображением (иногда каскадом). Маятник непрерывно движется от одного положения к другому и, следовательно, описывается динамической системой с непрерывным временем, т.е. потоком. Число насекомых, рождающихся каждый год в определённом ареале, или промежуток времени между каплями из подтекающего водопроводного крана более естественно описывать системой с дискретным временем, т.е. отображением.
Чтобы узнать, как развивается система из заданного начального состояния, нужно совершить бесконечно малое продвижение по орбите, а для этого можно воспользоваться динамикой (уравнениями движения). При таком методе объём вычислительной работы пропорционален времени, в течение которого мы хотим двигаться по орбите. Для простых систем типа маятника без трения может оказаться, что уравнения движения допускают решение в замкнутой форме, т.е. существует формула, выражающая любое будущее состояние через начальное состояние. Такое решение даёт «путь напрямик», т.е. более простой алгоритм, в котором для предсказания будущего используется только начальное состояние и окончательное время и который не требует прохода через все промежуточные состояния. В таком случае объём работы, затрачиваемой на прослеживание движения системы, почти не зависит от конечного значения времени. Так, если заданы уравнения движения планет и Луны, а также положения и скорости Земли и Луны, то можно, например, на много лет вперёд предсказать затмения.
Благодаря успешному нахождению решений в замкнутой форме для многих разнообразных простых систем на ранних стадиях развития физики появилась надежда, что для всякой механической системы существует такое решение. Теперь известно, что это, вообще говоря, не так. Непредсказуемое поведение хаотических динамических систем нельзя описать решением в замкнутой форме. Значит, при установлении их поведения у нас нет никакого «пути напрямик».
И всё-таки фазовое пространство даёт мощное средство для изучения хаотических систем, так как оно позволяет представить их поведение в геометрической форме. Так, в нашем примере маятника с трением, который в конце концов останавливается, его траектория в фазовом пространстве приходит в некоторую точку. Это неподвижная точка; так как она притягивает близлежащие орбиты, её называют притягивающей неподвижной точкой, или аттрактором (от англ. to attract — притягивать. — Перев.). Если сообщить маятнику небольшой толчок, его орбита вернётся в неподвижную точку. Всякой системе, которая с течением времени приходит в состояние покоя, отвечает неподвижная точка в фазовом пространстве. Это явление имеет весьма общий характер: потери энергии
| ||||||
Рис. 3. Аттракторы — это геометрические структуры, характеризующие поведение в фазовом пространстве по прошествии длительного времени. Грубо говоря, аттрактор — это то, к чему система стремится прийти, к чему она притягивается. Здесь аттракторы показаны синим цветом, а начальные состояния — красным. Траектории, выйдя из начальных состояний, в конце концов приближаются к аттракторам. Самый простой тип аттрактора — неподвижная точка (вверху слева). Такой аттрактор соответствует поведению маятника при наличии трения; маятник всегда приходит в одно и то же положение покоя независимо от того, как он начал колебаться (см. правую половину рис. 2). Следующий, более сложный аттрактор — предельный цикл (вверху в центре), который имеет форму замкнутой петли в фазовом пространстве. Предельный цикл описывает устойчивые колебания, такие, как движение маятника в часах или биение сердца. Сложному колебанию, или квазипериодическому движению, соответствует аттрактор в форме тора (вверху справа). Все три аттрактора предсказуемы: их поведение можно прогнозировать с любой точностью. Хаотические аттракторы соответствуют непредсказуемому движению и имеют более сложную геометрическую форму. Три примера хаотических аттракторов изображены в нижнем ряду; они получены (слева направо) Э. Лоренцем, О. Рёсслером и одним из авторов (Шоу) соответственно путём решения простых систем дифференциальных уравнений с трёхмерным фазовым пространством. | ||||||
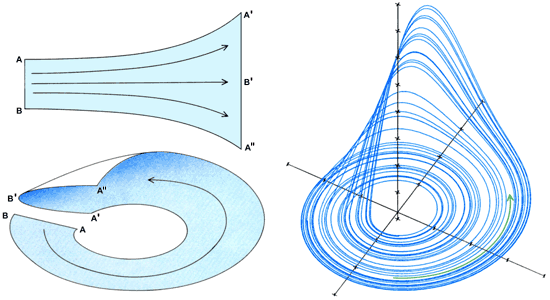 |
Рис. 4. Хаотический аттрактор имеет гораздо более сложное строение, чем предсказуемые аттракторы — точка, предельный цикл или тор. В крупном масштабе хаотический аттрактор есть неровная поверхность со складками. Показаны этапы образования хаотического аттрактора на примере аттрактора Рёсслера (справа). Сначала близкие траектории на объекте расходятся экспоненциально (вверху слева); расстояние между соседними траекториями увеличивается примерно вдвое. Чтобы остаться в конечной области, объект складывается (внизу слева): поверхность сгибается и её края соединяются. Аттрактор Рёсслера наблюдался во многих системах, от потоков жидкости до химических реакций; этот факт иллюстрирует максиму Эйнштейна о том, что природа предпочитает простые структуры. |
Некоторые системы не останавливаются по прошествии длительного времени, а циклически проходят некоторую последовательность состояний. Пример — часы с маятником, которые заводятся при помощи пружины или гирь. Маятник снова и снова повторяет свой путь. В фазовом пространстве его движению соответствует периодическая траектория, или цикл. Неважно, как маятник запущен в движение — в конце концов он придёт к тому же циклу. Такие аттракторы называются предельными циклами. Другой знакомой всем системой с предельным циклом является сердце. Одна и та же система может иметь несколько аттракторов. Если это так, то разные начальные условия могут привести к разным аттракторам. Множество точек, приводящих к некоторому аттрактору, называется его областью притяжения. Система с маятником имеет две такие области: при небольшом смещении маятника от точки покоя он возвращается в эту точку, однако при большом отклонении часы начинают тикать, и маятник совершает стабильные колебания.
Более сложный аттрактор имеет форму тора (напоминающую поверхность бублика). Такая форма отвечает движению, составленному из двух независимых колебаний, — так называемому квазипериодическому движению. (Физические примеры можно построить при помощи электрических осцилляторов.) Траектория навивается на тор в фазовом пространстве, одна частота определяется временем оборота по малому кругу тора, другая — по большому кругу. Для комбинации более чем двух вращений аттракторами могут быть многомерные торы.
Важное отличительное свойство квазипериодического движения состоит в том, что, несмотря на сложный характер, оно предсказуемо. Хотя траектория может никогда не повторяться точно (если частоты несоизмеримы), движение остаётся регулярным. Траектории, начинающиеся поблизости одна от другой на торе, так и остаются поблизости одна от другой, и долгосрочный прогноз гарантирован.
|
|
|
|||
|
|
|
|||
|
|
|
Рис. 5. Расходимость соседних траекторий является основной причиной того, что хаос ведёт к непредсказуемости. Идеальное измерение определяло бы точку в фазовом пространстве, но реальное измерение не бывает точным, порождая тем самым облако неопределённости. Истинное состояние может оказаться где угодно внутри этого облака. Как показано здесь на примере аттрактора Лоренца, неопределённость начального измерения представлена 10 000 красных точек, расположенных так близко друг к другу, что они неразличимы. По мере того как каждая точка движется в соответствии с уравнениями, облако вытягивается в длинную тонкую нить, которая затем многократно свивается, пока красные точки не распространятся по всему аттрактору. Предсказание стало невозможным: конечное состояние может быть в любом месте аттрактора. Напротив, для предсказуемого аттрактора все конечные состояния неизменно остаются поблизости друг от друга. Числа под картинками указаны в единицах, равных 0,005 с. | ||||||||||
| ||||||||||
Рис. 6. Хаотические аттракторы являются фракталами: объектами, проявляющими по мере увеличения всё большее число деталей. Хаос естественным образом порождает фракталы. Для того чтобы движение оставалось в конечной области, близлежащие траектории, хоть они и расходятся, должны в конечном счёте изогнуться и пройти поблизости друг от друга. Это повторяется снова и снова, порождая складки внутри складок, | ||||||||||
До недавнего времени были известны лишь перечисленные виды аттракторов: неподвижные точки, предельные точки, предельные циклы и торы. В 1963 году Э. Лоренц из Массачусетского технологического института открыл конкретную систему низкой размерности со сложным поведением. Движимый желанием понять, в чём трудность с прогнозами погоды, он рассмотрел уравнения движения жидкости (они описывают и атмосферные течения) и путём упрощений получил систему ровно с тремя степенями свободы.
Тем не менее эта система вела себя случайным образом и не поддавалась адекватному описанию с помощью
Промоделировав свою простую систему на компьютере, Лоренц выявил основной механизм, который вызывал случайное поведение: микроскопические возмущения накапливаются и влияют на макроскопическое поведение. Две траектории с близкими начальными условиями экспоненциально расходятся в процессе эволюции, так что они проходят рядом лишь совсем недолго. В случае нехаотических аттракторов качественная картина совершенно другая. Для них близкие траектории так и остаются близкими, небольшие ошибки остаются ограниченными, и поведение предсказуемо.
Ключ к пониманию хаотического поведения даёт простая процедура растягивания и образования складок в фазовом пространстве. Экспоненциальная расходимость — локальное явление: поскольку аттрактор имеет конечные размеры, две орбиты на хаотическом аттракторе не могут экспоненциально расходиться навсегда. Это означает, что такой аттрактор должен образовывать складки внутри самого себя. И хотя орбиты расходятся и следуют совершенно разными путями, в конце концов они должны пройти снова вблизи друг от друга. В результате орбиты на хаотическом аттракторе перемешиваются подобно тому, как перетасовываются карты в колоде. Случайность хаотических орбит есть результат этого процесса перемешивания. Вытягивание и образование складок происходит снова и снова, создавая складки внутри складок, и так до бесконечности. Иначе говоря, хаотический аттрактор является фракталом — объектом, в котором по мере увеличения выявляется всё больше деталей (см. рисунок справа).
Хаос перемешивает орбиты в фазовом пространстве точно так же, как пекарь месит тесто для выпечки хлеба. Представить себе, что происходит с близлежащими траекториями на хаотическом аттракторе, поможет такой эксперимент. Добавим в тесто каплю синей пищевой краски. Вымешивание теста — это комбинация двух действий: его то раскатывают (при этом цветное пятно расширяется), то складывают. Поначалу пятно просто становится длиннее, затем образуются складки, и всё это повторяется снова и снова. При ближайшем рассмотрении оказывается, что тесто состоит из многих слоев попеременно белого и голубого цвета. Уже через 20 шагов исходное пятно вытягивается более чем в
При наблюдении физической системы из-за неизбежных ошибок измерения нельзя точно задать её состояние. Одному состоянию отвечает не точка, а малая область в фазовом пространстве. Предельные размеры области устанавливает соотношение неопределённостей, но на деле различного рода шумы ухудшают точность измерений и способствуют появлению более заметных ошибок. Эта малая область аналогична синей капле в тесте.
Локализация системы в малой области фазового пространства, достигнутая путём измерения, даёт определённое количество информации об этой системе. Чем точнее проведено измерение, тем больше знает наблюдатель о состоянии системы. И наоборот, чем больше область, тем меньше уверенности у наблюдателя. Поскольку в нехаотической системе близко расположенные точки остаются близкими в процессе эволюции, часть информации, полученной измерением, сохраняется во времени. Именно в этом смысле такие системы предсказуемы: начальное измерение содержит информацию, которой можно воспользоваться для прогноза будущего поведения. Иначе говоря, предсказуемые динамические системы не особенно чувствительны к ошибкам измерения.
Вытягивание и складывание хаотического аттрактора систематически устраняет начальную информацию и заменяет её новой: при растяжении увеличиваются мелкомасштабные неопределённости, при складывании сближаются далеко отстоящие траектории и стирается крупномасштабная информация. Таким образом, хаотические аттракторы действуют как своего рода помпа, «подкачивающая» микроскопические флуктуации в макроскопическое проявление. Отсюда ясно, что никакого точного решения, никакого кратчайшего пути для прогноза будущего быть не может. Проходит совсем немного времени, и неопределённость, возникшая при начальном измерении, покрывает весь аттрактор, лишая нас возможности делать какие бы то ни было предсказания: между прошлым и будущим уже нет никакой причинной связи.
Хаотический аттрактор локально действует как усилитель шумов. Небольшая флуктуация, вызванная, быть может, тепловым шумом, очень быстро приводит к сильному отклонению траектории. Однако в одном важном отношении хаотические аттракторы отличаются от простых усилителей шумов. Поскольку предполагается, что вытягивания и складывания беспрерывно повторяются, малейшая флуктуация в конце концов приобретает важную роль в движении и качественное поведение не зависит от уровня шума. Поэтому хаотическую систему нельзя непосредственно «успокоить», скажем, понизив температуру. Хаотические системы сами по себе порождают случайность и не нуждаются во внешних случайных воздействиях. Случайное поведение таких систем объясняется не просто усилением ошибок и потерей способности предвидения; оно связано со сложными траекториями, образующимися при растягивании и складывании.
Следует отметить, что хаотическое поведение, как и нехаотическое, может возникать в консервативных недиссипативных системах. В этом случае орбиты «прикованы» не к аттрактору, а к энергетической поверхности. Однако диссипация играет важную роль во многих, если не во всех, системах реального мира, и можно ожидать, что понятие аттрактора окажется полезным в большинстве случаев.
Хаотические аттракторы низкой размерности открывают новую главу теории динамических систем, но спрашивается: имеют ли они
Изученная ими система представляла собой ячейку Куэтта, которая состоит из двух концентрических цилиндров. Пространство между цилиндрами заполнено жидкостью, и один из них или они оба вращаются с фиксированной угловой скоростью. По мере роста угловой скорости течение становится всё более сложным с весьма замысловатой зависимостью от времени (см. рис. 7). Голлуб и Суинни по существу измеряли скорость жидкости в некотором заданном месте. Увеличивая скорость вращения, они наблюдали переход от постоянной во времени скорости к периодически изменяющейся, а затем — к непериодически изменяющейся. В последнем переходе и заключалась суть эксперимента.
 a |
 b |
 c |
 d |
Рис. 7. Экспериментальные данные подтверждают гипотезу о том, что в основе некоторых типов случайных движений в жидкости лежат хаотические аттракторы. Здесь приведены сделанные друг за другом фотографии поверхности воды в ячейке Куэтта, состоящей из двух вложенных цилиндров. Пространство между цилиндрами заполнено водой, и внутренний цилиндр вращается с определённой угловой |
Этот эксперимент был придуман для того, чтобы подтвердить или опровергнуть одну из двух теоретических гипотез, которые предсказывали две разные картины поведения жидкости при изменении скорости вращения. Согласно теории Ландау, по мере увеличения скорости в жидкости должно было возбуждаться всё больше независимых колебаний. Соответствующим аттрактором был бы многомерный тор, С этим были несогласны Д. Рюэль из Института высших научных исследований (под Парижем) и Ф. Такенс из Гронингенского университета в Нидерландах. На основе математических соображений они пришли к выводу, что при движении жидкости появление аттрактора, соответствующего теории Ландау, маловероятно. Их результаты подсказывали, что любые возможные многомерные торы должны уступить место хаотическому аттрактору, как это и предполагалось с самого начала Лоренцем.
Голлуб и Суинни обнаружили, что при низких скоростях вращения течение жидкости не изменяется во времени: аттрактором является неподвижная точка. С увеличением скорости жидкость начинала колебаться с одной независимой частотой, отвечающей предельному циклу (периодическая траектория), а при дальнейшем увеличении возникло колебание с двумя независимыми частотами и соответствующим ему аттрактором — двумерным тором. Теория Ландау предсказывала, что и дальше всё должно происходить точно так же: постепенно будет появляться всё больше различных частот. Вместо этого при некоторой критической скорости вращения внезапно возникал непрерывный диапазон частот. Такое наблюдение больше согласовывалось с «детерминированным непериодическим течением» Лоренца, отдавая дань его идее о том, что в основе турбулентности лежат хаотические аттракторы.
Хотя анализ, проведённый Голлубом и Суинни, подкреплял представление, что некоторые случайные движения в потоках жидкости связаны с хаотическими аттракторами, их работа ничего не доказывала. Хотелось иметь более явное свидетельство о наличии в полученных экспериментальных данных простого хаотического аттрактора. Обычно в эксперименте регистрируются не все характеристики системы, а только некоторые из них. Например, Голлуб и Суинни не могли полностью регистрировать течение Куэтта; они измеряли только скорость жидкости в одной точке. Задача исследователя — воспроизвести аттрактор при помощи неполных данных. Ясно, что это не всегда возможно: если аттрактор слишком сложный,
Введенная нами методика, которой Такенс дал прочное математическое обоснование, позволяет воссоздать («реконструировать») фазовое пространство и искать хаотические аттракторы. Её основная идея состоит в том, что эволюция всякой отдельной компоненты системы определяется другими компонентами, с которыми она взаимодействует. Таким образом, информация о таких компонентах неявно содержится в «истории» отдельной компоненты. Чтобы воссоздать «эквивалентное» фазовое пространство, мы берём просто одну компоненту и обращаемся с измеренными значениями при фиксированных запаздываниях (например, секунду назад, две секунды назад
Эти «запоздалые» значения можно рассматривать как новые координаты, задающие точку в многомерном фазовом пространстве. Повторяя процедуру с другими интервалами запаздывания, получаем много таких точек. Затем другими приёмами можно проверить, лежат или не лежат эти точки на хаотическом аттракторе. Хотя такое представление во многих отношениях произвольно, оказалось, что оно сохраняет многие важные свойства аттрактора, которые, как выяснилось, не зависят от деталей реконструкции.
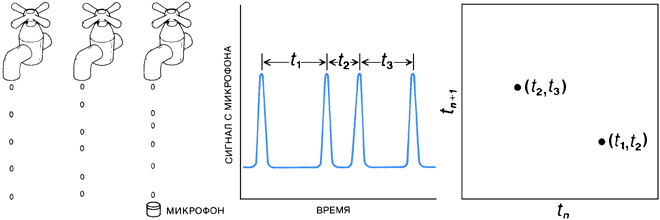
Для иллюстрации этой методики воспользуемся примером, который замечателен тем, что знаком и доступен почти каждому. Большинство людей осознают периодичность падения капель из подтекающего крана. Время между последовательными каплями может быть вполне регулярным, и не трудно угадать момент, когда упадёт следующая капля. Менее известно поведение крана при несколько большей скорости течения. Часто удаётся найти такой режим, что капли, хотя и продолжают падать по одной, создают никогда не повторяющийся перестук подобно бесконечно изобретательному барабанщику. (Этот эксперимент легко выполнить самому; лучше воспользоваться краном без насадки.) Смены периодических и случайных режимов напоминают переход от ламинарного течения к турбулентному. Быть может, за этой случайностью скрывается простой хаотический аттрактор?
Один из авторов (Шоу) в сотрудничестве с П. Скоттом, С. Поупом и Ф. Мартейном проводил экспериментальное изучение подтекающего крана в Калифорнийском университете
Эксперимент привёл к впечатляющему результату: в непериодическом режиме подтекающего крана действительно были найдены хаотические аттракторы. Случайное поведение капель могло бы вызываться
 |
|||||
|
|
|
|||
|
|
|
|||
Рис. 8. Подтекающий водопроводный кран служит примером привычной системы, которая может претерпевать хаотические изменения. Соответствующий аттрактор был «реконструирован» путём откладывания на осях интервалов между двумя последовательными каплями, как показано на верхних рисунках. Аттракторы, построенные для реальных водопроводных кранов, хорошо согласуются с аттракторами, построенными в соответствии с вариантами правила Хенона (b, d). (Аттрактор Хенона приведён на рис. 6.) Рисунки e и f были получены для больших скоростей течения и предположительно являются сечениями прежде невиданных хаотических аттракторов. На всех графиках по горизонтали отложено время tn между |
 |
 |
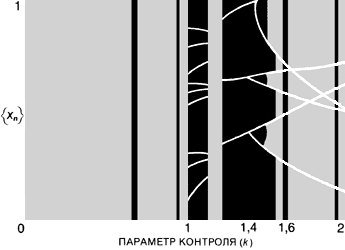
Рис. 9. Переход к хаосу схематически изображён в виде диаграммы бифуркаций: построен график семейств аттракторов (вертикальная ось) в зависимости от параметра управления (горизонтальная ось). Диаграмма соответствует простой динамической системе, отображающей одно число в другое. Использованная здесь динамическая система называется круговым отображением; оно задаётся итерационным уравнением
2π Для каждого значения параметра управления k на компьютере был построен соответствующий аттрактор. Цветом закодирована вероятность нахождения точек на аттракторах: красным закрашены часто посещаемые области, зелёным — те, которые посещаются не так часто, синим — редко посещаемые. Когда k растёт |
Если система хаотична, можно ли узнать, насколько она хаотична? Мерой хаоса служит «энтропия» движения, которая, грубо говоря, равна средней скорости растяжения и складывания или средней скорости, с которой «производится» информация2. Другой статистической характеристикой служит «размерность» аттрактора3. Поведение простой системы должно описываться в фазовом пространстве аттрактором малой размерности наподобие приведённых нами примеров. Чтобы задать состояние более сложной системы, может потребоваться несколько чисел, и в таком случае аттрактор может иметь более высокую размерность.
Методика реконструкции наряду с измерением энтропии и размерности позволяет
В последние несколько лет для многих систем со случайным поведением удалось найти простой хаотический аттрактор. Среди них — конвектив-ное течение в жидкости, нагреваемой в небольшом сосуде, колебание концентрации веществ при химических реакциях с перемешиванием, сокращение клеток сердца цыплёнка, а также колебательные процессы в большом числе электрических цепей и механических установок. Вдобавок тот же простой тип случайности был установлен для построенных при помощи компьютера моделей многих столь разнообразных явлений, как эпидемии, электрическая активность нервной клетки, пульсации звёзд. Сейчас идут эксперименты с целью найти хаос даже в таких несхожих вещах, как рождение блестящей идеи и экономика.
Следует, однако, подчеркнуть, что теория хаоса ни в коей мере не панацея. Движения систем со многими степенями свободы сложны и имеют случайный характер, и, даже если известно, что некая данная система хаотична, сам по себе этот факт мало что проясняет. Хороший пример — сталкивающиеся друг с другом молекулы в газе. Хотя известно, что такая система хаотична, это нисколько не облегчает предсказание её поведения. В движении участвует так много частиц, что можно надеяться лишь на статистическое описание, а основные статистические свойства выводятся без учёта хаоса.
Существуют другие неисследованные вопросы, для которых роль хаоса неизвестна. Что можно сказать о постоянно меняющихся пространственно протяжённых системах, таких, как дюны в Сахаре или достигшее полного развития турбулентное течение? Неясно, допускают ли сложные пространственно протяжённые системы удобное описание при помощи одного аттрактора в одном фазовом пространстве. Однако опыт обращения с простейшими аттракторами, быть может, подскажет более разветвлённую картину целых семейств пространственно мобильных детерминированных форм наподобие хаотических аттракторов.
Существование хаоса затрагивает сам научный метод. Классический способ проверки теории состоит в том, чтобы сделать предсказание и сверить его с экспериментальными данными. Но для хаотических явлений долгосрочный прогноз в принципе невозможен, и это следует принимать во внимание при оценке достоинств теории. Таким образом, проверка теории становится гораздо более тонкой процедурой, опирающейся больше на статистические и геометрические свойства, чем на подробное предсказание.
Хаос бросает новый вызов сторонникам редукционизма, которые считают, что для изучения системы её нужно разбить на части и изучать каждую часть. Эта точка зрения удерживалась в науке благодаря тому, что есть очень много систем, для которых поведение в целом действительно складывается из поведения частей. Однако хаос показывает нам, что система может иметь сложное поведение вследствие простого нелинейного взаимодействия всего нескольких компонент.
Эта проблема становится острой в широком диапазоне научных дисциплин, от описания микроскопических физических явлений и до моделирования макроскопического поведения биологических организмов. За последние годы сделан огромный шаг вперёд в умении подробно разобраться, какова структура той или иной системы, однако способность объединять собранные сведения в цельную картину зашла в тупик
Хаос часто рассматривают в свете налагаемых его существованием ограничений, таких, как отсутствие предсказуемости. Однако природа может пользоваться хаосом конструктивно. Через усиление малых флуктуаций она, возможно, открывает системам природы доступ к новизне. Быть может, жертва, ускользнувшая от хищника, чтобы не быть схваченной, воспользовалась хаотической регулировкой полёта как элементом неожиданности. Биологическая эволюция требует генетической изменчивости, а хаос порождает случайные изменения структуры, открывая тем самым возможность поставить изменчивость под контроль эволюции.
Даже процесс интеллектуального прогресса зависит от появления новых идей и нахождения новых способов увязывать старые идеи. Врождённая творческая способность, быть может, скрывает за собой хаотический процесс, который селективно усиливает малые флуктуации и превращает их в макроскопические связанные состояния ума, которые мы ощущаем как мысли. Иногда это могут быть
| 1. | Первым сильную неустойчивость систем с упругими столкновениями отметил Н. С. Крылов. Бильярдные системы общего типа, характеризующиеся свойством экспоненциальной неустойчивости траектории («бильярды Синая»), введены и изучены Я. Г. Синаем. назад к тексту |
| 2. | Существуют два вида энтропии, которые могут служить мерой хаоса: топологическая энтропия и метрическая энтропия (или энтропия Колмогорова–Синая). назад к тексту |
| 3. | Имеется в виду хаусдорфова размерность. назад к тексту |
| 1. | N. H. Packard, J. P. Crutchfield, J. D. Farmer and R. S. Shaw. Geometry from a time series. In: Physical Review Letters, 1980, v. 45, N 9, |
| 2. | R. Abraham and C. Shaw. Dynamics: the geometry of behavior. Aerial Press, P. O. Box 1360, Santa Cruz, Calif. 95061; |
| 3. | H. G. Schuster. Deterministic chaos: an introduction. VCH Publishers, Inc., 1984. |
| 4. | T. A. Bass. The eudaemonic pie: or why would anyone play roulette without a computer in his shoe? Houghton-Mifflin, 1985. |
| 5. | Dimensions and entropies in chaotic systems. (Edited by |
| 6. | Я. Г. Синай. Случайность неслучайного. Природа, 1981, № 3, |
|
Джеймс П. Кратчфилд (James P. Crutchfield), Дж. Дойн Фармер (J. Doyne Farmer), Норман X. Паккард (Norman H. Packard), Роберт С. Шоу (Robert S. Shaw), будучи ещё студентами-физиками старших курсов в Калифорнийском университете |