

| источник: —.”лам. "¬оспоминани¤ математика", –’ƒ, 2001 | источник: журнал "ѕрирода", 1988, є 7 | |
 |
 |
|
Introduction. In 1922 Norbert Wiener [1], treating the Brownian motion of a particle, introduced a measure on the space of continuous real functions, and a corresponding integral. In 1948 Richard Feynman [2], studying the quantum mechanics of a particle, introduced a different integral over the same space. He also showed that his integral can be used to represent the solution of the initial value problem for the Schrödinger equation. This suggested that the Wiener integral can likewise be used to represent the solution of the initial value problem for the heat equation, and Mark Kac [3, 4] showed this in 1949. Since then function space integrals have been used often in physics and studied extensively in mathematics.
We shall present an introduction to the Feynman integral, beginning with a heuristic definition of it in section 1. Then in section 2 we shall show that it solves the Schrödinger equation, and we shall define it for regions with boundaries in section 3. In section 4 we shall define it precisely. In the remaining sections we shall illustrate its use by evaluating it asymptotically. Our purpose is to show how function space integrals can be used to solve partial differential equations, and also how the application of mathematics has again led to the development of a new branch of mathematics.
Further information about the Feynman and Wiener integrals is contained in references [5]- [8] and [9], [10] respectively.
1. A heuristic definition of the Feynman integral. Suppose a particle of mass m is at position y on the x-axis at time t = 0, and that it has potential energy V(y). The particle may not remain at position y, but may move to position x at some later time t > 0. According to quantum mechanics, this move is not determinate, but it has a probability density p(x, t) of occuring. Furthermore p = K(x, t) 2, where K is a complex quantity called the probability amplitude. The probability amplitude K satisfies the Schrödinger equation
Eq. (1.1) is a linear partial differential equation for K which is of first order in / and of second order in x, so it is like the heat equation, but differs by having a factor i. Because solutions of (1.1) are wave-like, K is also called the wave function of the particle. Since the particle is surely at the position x = y when t = 0, K must satisfy the initial condition
(1.2) K(x,0) = 5(x-y).
The function δ(x –y) in (1.2) is the "delta function," which is supposed to be zero for x # y and to be infinite at x = y, in such a way that /^ S(x Ч y)f(y)dy = f(x) for any continuous function / Since there is no such function, S must be defined as a generalized function, as a distribution, or as a linear functional characterized by the above identity.
As an application, we shall use K to construct the solution ij/(x,t) of (1.1) which has the initial value ^(x,0) = ^0(X)- To do so we write K = K(x, y, t) to emphasize the dependence of K on y. Then we can write \j/ in the form
00
(1.3)
x, y, t)il/0(y)dy
oo
The fact that K satisfies (1.1) implies that \j/ does also, and the initial condition (1.2) implies that \j/(x9O) = \l/0(x).
There is a unique solution K of (1.1) satisfying (1.2), and it is called the Green's function or the fundamental solution of (1.1). In physics it is also called the propagator, because it describes how the particle travels or propagates from y to x. When the potential is V(x) = Ч (mco2/2)x2 where co is a constant, K can be found explicitly to be
(1.4) K(x9t) =
We shall now consider the problem of finding K for any

If the particle moves from y at time 0 to x at time t along a path z(t), then z(t) must be a single valued continuous function of t with z(0) = y and z(t) = x. Let P be the set of such paths. (See Fig. 1.) For each differentiable path z(t), we define the "action" S[z( Х ), i\ associated with that path from t = 0 to t = t. S[z( Х ), t] is just the integral of the particle's kinetic energy minus its potential energy:
(1.5)
Physical considerations [2, 8] suggest that a constant times exp{(///i)S[z( Х), r]} is the propagator associated with the path z( Х). Then, in view of the probabilistic interpretation of the propagator, it is natural to represent K as the sum of the propagators associated with all the paths in P. Thus we write
(1.6) K(x,t) = j expjy S[z( Х ),r]jDz( Х ).
Eq. (1.5) gives the Feynman path integral representation of the solution K of (1.1) and (1.2). The right side is supposed to be an integral over the set P of continuous paths from (y,0) to (x, i). It is symbolic, because the integrand has been defined only for differentiable paths, and the integral has not been defined at all. Therefore we shall now try to define it.
In order to define S\z{ Х ), t] for any continuous path, we shall represent the derivative dzjdt in (1.5) by a difference quotient. At the same time, we shall replace the integral by a finite sum which approximates it. To do so we divide the interval (0,0 into N equal parts, each of length At = t/N, with division points tj = jAt, j = 0,1,",N. Let Zj = z(tj). Then we replace the integral (1.5) for S by the sum
(1.8) K(x,t)
The normalization factor in (1.8) can be found by physical considerations.
The right side of (1.8) is the definition of the Feynman integral or path integral in (1.6). Although (1.6) is an integral over paths, (1.8) does not involve paths. Instead the variables Zj in (1.8) are independent variables of integration. Since (1.8) results from integration over all paths, it is not surprising that no particular path occurs
* ' A.
in it.
Let us apply (1.8) to the quadratic potential V(x) = Ч mco2x2/2. In that case the exponent of the integrand is quadratic, so the integration involves Gaussian functions and it can be done explicitly. Then the limit is exactly the result (1.4). (See [2], [5], [8].) Thus for quadratic potentials, (1.8) is correct. The question whether (1.8) is correct for some larger class of potentials has not yet been decided.
If we set m = 2hi, and replace K(x, t) by W(x, t), (1.8) becomes
exp (1.9)
This is just the conditional Wiener integral of
exp
h
which is a functional of the path z ( Х ). The integral is called conditional because it involves only paths which satisfy the conditions z(0) = y and z(f) = x.
2. The integral satisfies the Schrödinger equation. To show that (1.8) is correct for any V(x), we shall show that the integral satisfies (1.1) and (1.2). Then because that problem has a unique solution K, it will follow that (1.8) is correct. Since our demonstration will be formal, it will be a plausibility argument for (1.8) rather than a proof. For simplicity we shall set h = 1 and m = 1/2 in this and the next section.
We begin by letting KN(x,t) denote the expression under the limit in (1.8), so that K = limjv^ KN. Then we can rewrite KN as a single integral of Xjv-i as follows:
(2.1) KN(x,t)
= (4niAt)~1/2
In the normalization factor we have set t/N = At. Next we expand KN-t as a finite Taylor series in powers of x Ч zN_l9 about x. By using this expansion in (2.1), we obtain
,'♦00
(2.2) K*(x,t) - (47r/Ar)~1/2exp[ - iV(x)At~] exp
J ~ 00
Ч (x Ч zN_ 1 + 0[(x - zN_x
The notation 0(zn) denotes a function /(z) which satisfies |/(z) constant A and some neighborhood z < (5 of z = 0. In (2.2) it refers to the remainder of the Taylor series.
In (2.2), KN is expressed as the sum of four integrals. The first three are just the first three moments of a Gaussian distribution, so they can be evaluated explicitly. The second integral vanishes because its integrand is odd, and so does the integral of the cubic term in the remainder. Therefore only the first and third integrals contribute, and the order of the remainder is determined by the integral of the fourth degree term. Upon using the values of these integrals in (2.2), we get
(2.3) KN(x,t) = exp[ - i
Now we expand the exponential in powers of At and rearrange (2.3) into the form (2.4) ^-t[KN(x,t) - KN-
+ O(At).
As N -► oo, both KN_1 and KN tend to K, while tN_t tends to t and At tends to zero. Since tN.x = t - At, the left side of (2.4) tends to idtK(x,t). Thus the limit of (2.4) is just the Schrödinger equation (1.1), so the path integral satisfies this equation.
To show that the path integral also satisfies the initial condition (1.2), we observe that when t tends to zero, At = tjN also tends to zero. Therefore, in finding the limit of K at t = 0, the term V(zj + 1)At in the exponent in (1.8) can be omitted. The resulting integral is just the integral of a Gaussian function, which can be evaluated explicitly. Then the limit in (1.8) is found to have exactly the initial value (1.2). (See Buslaev [11].) This completes the formal demonstration that (1.8) is correct. More detailed discussions of this demonstration, as well as the construction of (1.8), are given in [2], [7], [8], [11] and [12].
3. Boundaries and reflection. The Feynman integral representation (1.8) of K can be extended to n dimensions by letting x, y and zy denote points in n dimensional space, and performing all integrations over that space. In addition an extra normalization factor must be introduced. Although this extension is straightforward, the extension to a region with a boundary is more subtle, as we shall now see.
Let K+(x, t) satisfy the Schrödinger equation in a domain D+ exterior to a closed surface B in n dimensional Euclidean space. Then the problem solved by K+ is the following, if K+ vanishes on S:
dK h2
fjO
(3.3) K+(x,t) = 0, x on B.
If instead of K+ = 0 on B, the normal derivative of K+ vanishes on B, (3.3) must be changed accordingly.
To solve this problem we introduce a copy of D+ which we call Z>_, and we join D+ to D_ along their common boundary B. In this way, we obtain a two sheeted space D, composed of the sheets D+ and Z>_, which has no boundary. (See Fig. 2.) Let us denote by K(x9 y, t) the solution of (3.1) and (3.2) for x and y in D. We require K and its normal derivatives to be continuous on B, where the two sheets join. We shall now show that in terms of K, we can write K+ in the form
(3.4) K+(x+9 y+, 0 = K(x+, y+, 0 - K(x+, y_, t).
Here x+ and y+ denote points in D+ while x_ and y_ are the corresponding points
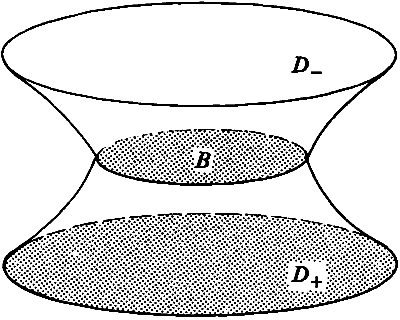
To show that (3.4) is correct we first observe that K+ defined by (3.4) satisfies (3.1). This is because both terms on the right satisfy (3.1) in D, and D contains D+. To see that (3.2) holds we note that the first term on the right tends to d(x+ Ч y+) as t -► 0 while the second term tends to Ч d(x+ Ч y_). Therefore, for x+ in D+, the second term vanishes as t -► 0, so (3.2) is satisfied. Finally we observe that K+ = 0 for x+ on B because the two terms on the right side of (3.4) are equal when x+ is on B, and they cancel. Similarly, when the minus is replaced by a plus sign |in (3.4), the normal derivative of K+ vanishes on B by symmetry.
We now represent K by a Feynman integral, which we can do as before since K is defined in D, which has no boundary. In performing the integration over the zy in the definition of the integral, we integrate over D, i.e., over D+ and D_. In this way we include all paths in D. When we use this integral representation of K in (3.4), we obtain a representation of K+.
The use of a double sheeted space to solve boundary value problems was introduced by Sommerfeld in 1896 in solving a diffraction problem. Buslaev [11] first used it together with function space integrals to obtain representations of solutions of boundary value problems for parabolic partial differential equations.
4. Rigorous definition of the Feynman integral. The Feynman integral (1.8) can be obtained from the Wiener integral (1.9) by replacing At in the Gaussian distribution and in the normalization constant by Ч lihAt/m. This corresponds to introducing a Gaussian distribution with an imaginary variance. Now the Wiener integral can be defined in terms of a Wiener measure over the space of continuous functions. This measure involves the Gaussian distribution [5]. Therefore it is natural to suppose that the Feynman integral can also be defined in terms of a measure, but a complex measure involving a Gaussian distribution with a complex variance.
In 1960 Cameron [13] showed that no such countably additive measure exists. To date, there is no measure-theoretic definition of the Feynman integral. There are, however, several definitions of it which do not use measure. One of the simplest of these is that of Nelson [14], which we shall now present.
Let L2(R) denote the Hilbert space of complex valued Lebesgue square integrable functions on the real line R. In this space we seek the solution ^(t) of the following initial value problem for the Schrödinger equation:
¥(0) =
Here H = Ч d* is a second order differential operator and V denotes multiplication by the real function V(x).
The operator H is self adjoint if its domain D(H) is properly restricted. Similarly, the operator V is self adjoint on the domain D(f) of all *¥ eL2(R) such that K*F is also in L2(R). Kato (see [14]) has shown that the operator H + V is self adjoint on the domain D(H) if V(x) e LP(R) with p ^ 2. Since each of the three operators (H, V, H + V) is self adjoint, the spectral theorem guarantees the existence of the following unitary operators:
Gr = exp(- itH), Wf = exp(- itV), Kf = exp(-/*[#+ VI).
In terms of Kf the solution *F(0 can be written as
(4.1) ¥(0 = Ktx¥0 = exp [ - it(H +
To utilize (4.1), we apply the Trotter-Kato Product Formula [14] to express Kl in terms of Gf and W\
(4.2) Kty¥0 = lim (Wt/NGt/N)Nx¥
0,
N-*co
To make (4.2) more explicit, we use the Fourier integral representation of ^(x to express (Gtx¥0)(x) in the form
(G"P0)(x) =
= ^ ! e-ipxeip2t¥0(p)dp.
Here ^(p) is tne Fourier transform of ^(x). Using the definition of ^(p), inter changing the order of integration, which is permissible, and then evaluating the integral with respect to p, we obtain
= i_ f∞∞ їpo(x') f ∞∞ eip2teiplx'~x)dpdx'
^71 J-oo J-oo
p 00 JЧ 00
Now we use this expression for Gtx¥0 in (4.2) and (4.1) to obtain
f ∞∞ / N \
exp
X
We can rewrite this in the equivalent form
where zN + i = x.
When we can exchange the order of integration and of taking the limit in (4.3), the coefficient of *Fo(zo) becomes exactly the expression for K in (1.8) with h = 1 and m = 1/2. To see that this coefficient is equal to the fundamental solution K(x,zo,t)9 we just compare (4.3) and (1.3). This comparison yields the Feynman integral representation (1.8) of K.
Equation (4.3) defines the Feynman integral representation of the solution operator K* as the strong limit of a sequence of linear operators acting in the Hilbert space L2(R). This definition utilizes the semigroup property of K\ the same property which is the basis for the formal verification given in Section 2. Other definitions of the Feynman integral, which also depend upon this semi-group property, have been given by Cameron, Babbitt, and Feldman and Nelson (see [14]). Recently, C. DeWitt [16] has given a definition which is almost measure-theoretical. However, no definition has permitted justification of the interchange of Feynman integration with other integrations, with limits, etc.
5. Asymptotic evaluation of Feynman integrals. We shall now evaluate the Feynman integral (1.8) asymptotically for h small by the method of stationary phase. First we shall explain the method by applying it to the single integral
(5.1)
in which s(z) is a thrice continuously differentiate real valued function. As h tends to zero, the exponential function oscillates more and more rapidly. Consequently contributions to the integral from each subinterval of (a, b) tend to cancel out, and the integral tends to zero. The largest contribution will come from that subinterval in which the oscillation is slowest. That subinterval will be the neighborhood of a point z at which s'{z) = 0. Since s(z)/h is the phase of the integrand, and since s is stationary at z, z is called a point of stationary phase. Let us suppose that there is exactly one such point in (a, b), and that it is an interior point.
We now introduce the new integration variable ( = h~1/2(z Ч z) so that z = z + hl!% Then s(z) = s(z + h1/2Q = s(z) + (fe/2)CV(z) + O(h3/2)9 since s (z) = 0. By using this expansion of s, we can write (5.1) in the form
(5.2) K(h) = /z1/2exp -y-s(z) exp
As h tends to zero, the limits of integration tend to ± oo. The integral of a Gaussian function from Ч oo to + oo is known, so (5.2) becomes
(5.3) K(h)
[2nh - [s\z\
U
Although our calculation is formal, the result (5.3) can be proved to be correct [17]. In applying the method of stationary phase to the Feynman integral, we shall use the symbolic form (1.6) because of its similarity to (5.1). The phase Sis a functional of the path z(t), so its derivative is a functional derivative. Equating it to zero yields a differential equation for the stationary path z(t), as we shall now show. First we introduce the new variable £(t) = /z~1/2[z(t) Ч z(t)], which satisfies ((0) = C(0 = 0. Now we set z(x) = z(t) + /z1/2C(t) in (1.5), and expand S[z( in powers of /z1/2, obtaining
(5.4) S[z(
The h1/2 term in (5.4) is linear in (, and is called the first variation of S. Equating it to zero, after integrating the first term in it by parts, yields
(5.5) h1/2 f im^r + V'\z(xy]\t(x)dx = 0.
Jo I dx2 J
We want the first variation (5.5) to vanish for every continuous function £(t) which satisfies £(0) = £(0 = 0. Therefore the coefficient of £(t) in the integrand, which is the functional derivative of S[z( Х ),t], must vanish:
(5.6) m~+K'[z(T)]=0.
This is just Newton's equation of classical mechanics for the stationary path z(t). In order that z be in P, it must also satisfy the boundary conditions
(5.7) z(0) = y, z(t) = x.
For simplicity we shall assume that (5.6) and (5.7) have a unique solution. It is just the path from (j>,0) to (x, 0 given by classical mechanics. We now use (5.4) and (5.5) in (1.6) to get
(5.8) K(x,t) = expj-i-S[z( Х )],*} Jexp [y [' {^^J " ^PWFw}^
The integration is over paths £(t) from £ = 0atT = 0to£ = 0ati = £. The exponent in the integrand of (5.8) is quadratic in f and d^jdx, so the corresponding form (1.8) contains only integrals of Gaussian functions. When the integration is performed and the limit N -> oo taken, the result is K(x,t) = Kc(x, 0[l + 0(/z1/2)] where Kc is given by
(5.9) Ke(x9t) =
Here s(x, y, t) = S[z(t), t] and M is the number of zeros, counted according to order, of s(x, y, t) in the open interval 0 < t < t. C. Morette [12] was the first to get Kc from the Feynman integral, although Feynman [2] indicated the connection. When there are several classical paths z, Kc is a sum of terms of the form (5.9), one for each path.
The subscript c on Kc stands for classical, because 5 is just the action associated with the classical path z(t), and Kc is determined entirely by s. The asymptotic form of K given by (5.9) can also be derived directly from the differential equation (1.1) by the W.K.B. method. It is not valid at the zeros of sxy, which are the caustics of the classical paths through (y, 0). The phase factor e~tMn/2 represents a phase loss of amount tt/2 for each of the M times the path z(t) touches a caustic. By using such considerations, Keller [18] and Maslov [19] introduced the index M for any dimension, and Arnold [20] showed that it is the Morse index of a certain multisheeted space on which sx(x, y, t) is single valued.
When the above method of asymptotic evaluation is applied to the Feynman integral representation of K+, given by (3.4), it yields (5.9) for the direct classical path from y to x plus a similar term for the reflected classical path from y to the boundary B to x. A refined evaluation by Buslaev [11], yields another term corresponding to a classical path from (y, 0) which touches B tangentially, proceeds along a geodesic on B, and leaves B tangentially on a classical path to (x, t). (See Fig. 3.) This path is precisely a surface diffracted ray, which occurs in Keller's [21] geometrical theory of diffraction, and the term is exactly the value of the solution associated with that ray.

6. The time independent Schrödinger equation. The wave function ij/(x91) of a particle of energy E is of the form e~lEt/hu(x). It follows from (1.1) that u(x) satisfies the time-independent Schrödinger equation, obtained from (1.1) by replacing ihd/dt by E. The Green's function G(x, y, E) of this equation is defined as follows:
2m dx2
V(x) - E
G(x, y,E) = - d(x - y),
lim
dG
- + ikG
dx
= 0.
The last condition is called the radiation condition because it guarantees that G contains only waves radiating to infinity, and none coming in from infinity. In it k = (imE/h2)112. One of the reasons for studying G is that it is the kernel of the resolvent of the Schrödinger operator.
If E is replaced by E + irj with r\ > 0, then G(x, y, E + irj) is readily seen to be the Fourier transform of K:
G(x, y,E +
1 f∞∞
exp
h
K(x, y, t)dt, rj > 0.
By using the Feynman integral representation of K in the Fourier integral, we obtain the following integral representation of G:
(6.1) G(x,y,E) = 4 lim f∞∞ f exP 4-
in
)dt.
We shall now evaluate G asymptotically as h -> 0 by applying the method of stationary phase to the integral representation (6.1). Since (6.1) involves integration over paths and over t, we must find a pair z(t) and t which make the phase stationary. By proceeding as we did in the last section, we find that z(t) must satisfy Newton's equation (5.6) and the boundary conditions (5.7) with t replaced by i. We also obtain the condition dS[z( Х )J~]jdf = Ч E to make the phase stationary with respect to f.
This condition, which serves to determine t, can be written explicitly as
(6.2)
a. r
3f Jo
ї(<*>
dx = - E.
The derivative of the integrand with respect to t in (6.2) vanishes as a consequence of (5.6) and (5.7). Therefore (6.2) yields the following equation with t = f:
(6.3)
From (5.6) it follows that the left side of (6.3) is independent of t, so (6.3) holds for
o ^ t <; f.
By using (6.3) at t = 0 we can determine two possible values of the initial velocity dz(0)/dT. These velocities and the initial condition z(0) = y yield two solutions z(t) of (5.6). If one of these paths z(t) passes through x, then i is determined by z(t) = x and that path is a stationary path which yields a contribution to the integral (6.1). If both trajectories pass through x they are both stationary paths and the integral is asymptotically equal to the sum of their two contributions. If neither passes through x, then there is no stationary path and the integral is asymptotically equal to zero. If a trajectory passes through x more than once, it makes a contribution to the integral for each such passage, and the integral is asymptotically equal to the sum of all of them. We shall illustrate all these possibilities.
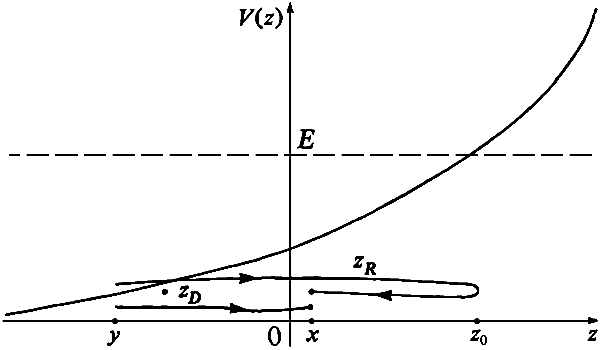
Let us first suppose that the potential V(z) is a continuous monotone increasing function of z with V( Ч oo) = 0 and V( + oo) = +00 as in Figure 4. Then for any E > 0 there is a unique solution z0 of the equation V(z0) = E. The point z0 is called a "turning point," because the velocity of a particle vanishes there and changes sign in its neighborhood, as we see from (6.3). Now let us assume that y < z0. Then if x > z0, no trajectory from y passes through x. However, if x < z0 there are two trajectories from y to x, a direct one zD(%) and a reflected one zR(%) which has been reflected at z0. (See Figure 4.) We obtain the contributions of these paths to the integral (6.1) by writing the integral as a sum of two integrals, each of which contains just one of these paths. Then we expand the exponent of each integrand to second order about the stationary path, evaluate the resulting Gaussian integral and let rj tend to zero.
In this way we find that as h tends to zero, G(x, y, E) ~ Gc(x, y, E) where Gc is defined by Gc(x, y,E) = 0, y < z0 < x, and
(6.4)
_ 1
cxp
If x < y < z0, Gc is given by the above expression with x and y interchanged in the first integral. In (6.4) p(x) is the classical particle momentum defined by p(x) = + [2m{E- F(x)}]1/2. The quantity Gc is the leading term in the "classical," "geometrical optics," or "time-independent W.K.B." approximation to G.
Now we suppose that F(x) is monotone decreasing for x < 0 and monotone increasing for x > 0 with F( + oo) = + oo and F(0) = 0. Then for each E > 0 there are exactly two turning points zl and zr satisfying V(z) = 0, with zl < zr. If y lies in the interval (z/5 zr) and x lies outside it, there is no trajectory from y passing through x. However, if x also lies in the interval, the two trajectories from y pass through x infinitely many times as they reflect back and forth between zt and zr. Thus G ~ Gc where Gc is an infinite series of terms like those in (6.4). Apart from a factor, the series is the geometric series
00
(6.5) S [ - et9r\" = (1 + eir
where Ѓ(E) is defined by
(6.6) O(£) = y( l2miE - V(z)}]1/2dz.
J Zj
The series (6.5) diverges when <D = (2n + \)n where n is an integer. Since G is the kernel of the resolvent operator, its poles as a function of E are the eigenvalues of the Schrödinger equation. Thus the poles of Gc(x,y,E) are asymptotic to the eigenvalues as h -> 0. Therefore the asymptotic form of the nth eigenvalue is the root En of the equation
(6.11) A [ ' [2m{£ - V(z)}Y/2dz = (2n + 1)tt, h = 0,1, ХХХ.
This equation for En was found before the discovery of the Schrödinger equation, and it is called the Bohr–Sommerfeld quantum condition. Further details of these calculations are given in [23] and [24].
7. Further developments. We have seen that the Feynman integral can be extended readily to n dimensional space when Cartesian coordinates are employed, but it is more difficult to extend it in other coordinate systems [2]. It has also been extended to complex t by McLaughlin [22], and used by him to obtain both regular and singular asymptotic expansions of solutions of the Schrödinger equation [23].
Function space integral representations have also been found for the solutions of the wave, Klein-Gordon, Pauli, Dirac and quantized field equations ([5], [6]). No asymptotic evaluations of the integrals for the latter three equations have been made because their integrands involve non-commuting matrices. Path integrals employing a Hamiltonian instead of a Lagrangian have also been introduced [24].
Schulman [25] has obtained a path integral representation of the solution of the Pauli equation by using a path integral for the solution of the Schrödinger equation on the group manifold of SU(2). The latter integral reduces exactly to a sum over those paths which satisfy Newton's equations of motion. This is also true for the quadratic potential in Euclidean space. Dowker [26] showed that the same reduction occurs on the group manifold of any compact semi-simple Lie group. Eskin [27] proved the corresponding result for the heat equation on any symmetric space whose group of motions is a complex semi-simple Lie group.
Many other applications of the Feynman integral can be found in the references we have cited and in numerous other papers. In addition the references describe still more developments of the theory from both a physical and a mathematical point of view. Although a great deal has been accomplished, there are many important problems concerning the Feynman integral which are still unsolved.
Research supported by the Office of Naval Research under Contract No. N00014-67-A-0467-0015 and by NSF Grant GP37627.
| 1. | N. Wiener, The average value of a functional, Proc. London Math. Soc., 22 (1924) |
| 2. | R. P. Feynman, Space-time approach to non-relativistic quantum mechanics, Rev. Mod. Phys., 20 (1948) |
| 3. | M. Kac, On distributions of certain Wiener functionals, Trans. Amer. Math. Soc., 65 (1949) |
| 4. | ——, On some connections between probability theory and differential equations, Proc. of Second Berkeley Symposium on Math. Statistics and Probability, (1951) |
| 5. | I. M. Gelfand and A. M. Yaglom, Integration in functional spaces and its applications in quantum physics, J. Math. Phys., 1 (1960) |
| 6. | S. G. Brush, Functional integrals and statistical physics, Rev. Mod. Phys., 33 (1961) |
| 7. | M. Kac, Probability and Related Topics in Physical Sciences, Lectures in Applied Mathematics, Boulder, 1957. [–усский перевод здесь. |
| 8. | R. P. Feynman and A. R. Hibbs, Quantum Mechanics and Path Integrals, McGraw-Hill, New York, 1965. |
| 9. | Yu. L. Daletskii, Functional integrals connected with operator evolution equations, Russian Math. Surveys, 17 (1962) |
| 10. | E. W. Montroll, Markov chains, Wiener integrals, and quantum theory, Comm. Pure Appl. Math., 5 (1952) |
| 11. | V. S. Buslaev, Continuum integrals and the asymptotic behavior of the solutions of parabolic equations as |
| 12. | C. Morette, On the definition and approximation of Feynman's path integral, Phys. Rev., 81 (1951) |
| 13. | R. H. Cameron, A family of integrals serving to connect the Wiener and Feynman integrals, J. Math. and Phys., 39 (1960) |
| 14. | E. Nelson, Feynman integrals and the Schrödinger equation, J. Math. Phys., 5 (1964) |
| 15. | E. J. McShane, Integrals devised for special purposes, Bull. Amer. Math. Society, 69 (1963) |
| 16. | C. Morette DeWitt, Feynman's path integral. Definition without limiting procedure, Comm. Math. Phys., 28 (1972) |
| 17. | E. T. Copson, Asymptotic Expansions, Cambridge Tracts in Math. and Math. Phys., 55, Cambridge University Press, 1965. |
| 18. | J. B. Keller, Corrected Bohr–Sommerfeld quantum conditions for nonseparable systems, Annals of Physics, 4 (1958) |
| 19. | V. P. Maslov, Perturbation theory and asymptotic methods (in Russian), Moskov. Gosud. Univ., Moscow 1965; French translation, Dunod, Paris (1972). |
| 20. | V. I. Arnold, On a characteristic class entering in the quantization conditions. Functional Analysis and its Applications, 1 (1967) |
| 21. | J. B. Keller, A geometrical theory of diffraction, Amer. Math. Soc., Calculus of Variations and Its Applications; McGraw-Hill, New York, 1958, |
| 22. | D. W. McLaughlin, Complex time, contour independent path integrals, and barrier penetration, J. Math. Phys., 13 (1972) |
| 23. | ——, Path Integrals, asymptotics, and singular perturbations, J. Math. Phys., 13 (1972) |
| 24. | M. Gutzwiller, Phase-integral approximation in momentum space and the bound states of an atom, J. Math. Phys., 8 (1967) |
| 25. | L. S. Schulman, A path integral for spin, Phys. Rev., 176 (1968) |
| 26. | J. S. Dowker, Quantum Mechanics on group space and Huygen's principle, Annals of Physics, 62 (1971) |
| 27. | L. D. Eskin, The heat equation and the Weierstrass transform on certain symmetric Riemannian spaces, A.M.S. Translations, 75 (1968) |