В МИРЕ НАУКИ Scientific American · Издание на русском языке № 8 · СЕНТЯБРЬ 1988 · С. 42–48

Случайность в арифметике



Невозможно доказать, конечное или бесконечное число решений имеет каждое уравнение из семейства алгебраических уравнений: ответ варьирует случайным образом, и, следовательно, не может быть найден с помощью математического рассуждения

ГРЕГОРИ ДЖ.ЧЕЙТИН

Что может быть бесспорнее того факта, что 2 плюс 2 равняется 4? Со времён древних греков математики считали, что более несомненной вещи, чем доказанная теорема, не сыскать. Действительно, математические утверждения, истинность которых может быть доказана, часто считались более надёжным основанием для системы мышления, чем любой моральный или даже физический принцип. Немецкий философ и математик XVII века Готфрид Вильгельм Лейбниц считал возможным создать «исчисление» рассуждений, которое когда-нибудь позволит улаживать все споры с помощью слов: «Давайте вычислим, господа!». К началу нашего столетия прогресс в разработке символической логики дал основание немецкому математику Давиду Гильберту заявить, что все математические вопросы в принципе разрешимы, и провозгласить окончательную кодификацию методов математического рассуждения.

В 30-е годы нашего столетия этот оптимизм совершенно развеялся под влиянием удивительных и глубоких открытий К. Гёделя и А. Тьюринга. Гёдель доказал, что не существует системы аксиом и методов рассуждения, охватывающей все математические свойства целых положительных чисел. Позднее Тьюринг облёк остроумные, но сложные гёделевы доказательства в более понятную форму. Как показал Тьюринг, гёделева теорема о неполноте эквивалентна утверждению, что не существует общего метода для систематического принятия решения о том, остановится ли когда-нибудь компьютерная программа, т.е. приведёт ли она когда-нибудь компьютер к остановке. Разумеется, если некоторая конкретная программа приводит к остановке компьютера, этот факт легко может быть доказан непосредственным выполнением этой программы. Трудность заключается в доказательстве того, что произвольно взятая программа не останавливается.

ДАВИД ГИЛЬБЕРТ (1900): «Любая определённая математическая задача должна обязательно поддаваться точному решению, либо в виде непосредственного ответа на заданный вопрос, либо в виде доказательства невозможности её решения и, кроме того, неизбежности неудач всех попыток её решения... Однако, как бы трудны эти проблемы ни казались нам, и как бы ни были мы беспомощны перед ними, у нас имеется тем не менее твёрдая уверенность в том, что их решение будет получено в результате конечного числа чисто логических процессов... Мы слышим внутри нас постоянный призыв: "Вот проблема, ищи решение. Ты можешь найти его с помощью чистого мышления...".»

КУРТ ГЁДЕЛЬ (1944): «Оказалось, что решение некоторых арифметических задач требует использования предложений, по существу выходящих за рамки арифметики. Разумеется, в подобных обстоятельствах математика может потерять часть своей «абсолютной истинности», но под влиянием современной критики оснований это происходило не раз...»

Фундаментальная разрешимость всех вопросов математики была заявлена Д. Гильбертом (на снимке ему около 50 лет). Гильберт считал, что конечной системы аксиом и правил рассуждения достаточно для доказательства истинности или ложности всех теорем. Фундаментальная неразрешимость математических вопросов была доказана К. Гёделем. На снимке, сделанном А. Ньюменом, ему около 50 лет. Гёдель опубликовал своё доказательство в 1931 г.; в ту пору ему было 25 лет, а Гильберту — 70.

Недавно мне удалось сделать ещё один шаг по пути, намеченному Гёделем и Тьюрингом. Преобразовав некоторую конкретную компьютерную программу в алгебраическое уравнение такого типа, который был знаком ещё древним грекам, я показал, что область чистой математики, известная под названием теории чисел, содержит в себе случайность. Это исследование демонстрирует, говоря словами Эйнштейна, что Бог порой использует целые числа для игры в кости.

Полученный результат, входящий составной частью в то, что было названо алгоритмической теорией информации, не является причиной для пессимизма; он не вносит в математику анархию. (В самом деле, большинство математиков продолжают работать над своими проблемами, как и раньше.) Он означает лишь, что в некоторых ситуациях должны применяться математические законы особого рода — статистические. Подобно тому как физика не в состоянии предсказать, в какой именно момент распадётся данный атом радиоактивного вещества, математика порой бессильна дать ответ на некоторые вопросы. Однако физики могут надёжно предсказать средние значения физических величин, отнесённые к большому количеству атомов. Математики в некоторых случаях должны, вероятно, ограничиваться таким же подходом.

Моя работа служит естественным продолжением работы Тьюринга, однако если Тьюринг анализировал, остановится или нет произвольная программа, я рассматриваю вероятность того, что универсальный компьютер прекратит работу, если его программа выбрана совершенно случайно. Что я имею в виду, говоря «выбрана совершенно случайно»? Поскольку любая программа может быть сведена к последовательности двоичных разрядов — битов (каждый из которых может принимать значение 0 или 1), «считываемых» и «интерпретируемых» компьютером, смысл упомянутой фразы состоит в том, что совершенно случайная программа, состоящая из n битов, эквивалентна результату n бросаний монеты (где «орёл» представляется нулём, а «решка» — единицей, или наоборот).

Вероятность того, что такая совершенно случайная программа остановится (обозначим эту вероятность символом Ω), выражается вещественным числом, заключённым между 0 и 1. (Утверждение Ω=0 будет означать, что никакая случайная программа не остановится, a Ω=1 — что всякая случайная программа остановится. Если мы имеем дело с универсальным компьютером, ни одно из этих крайних значений не реализуемо.) Поскольку Ω — вещественное число, полностью представить его можно лишь как бесконечную последовательность разрядов. В двоичной системе это последовательность нулей и единиц.

Наверное, самым интересным свойством этой бесконечной цепочки является то, что она алгоритмически случайна: она не может быть сжата в программу (рассматриваемую как цепочка битов) длиной, меньшей чем она сама. Это определение случайности, играющее основную роль в алгоритмической теории информации, было независимо сформулировано в середине 60-х годов советским академиком А. Н. Колмогоровым и мною. (Впоследствии это определение мне пришлось подправить.)

Основная идея такого определения проста. Некоторые последовательности битов могут быть сжаты в программы, более короткие, чем сами эти последовательности, потому что они построены по какой-либо схеме или подчиняются какому-либо правилу. Например, 200-битовая последовательность вида 0101010101... может быть сильно сжата, если её задать как «100 повторений пары 01». Безусловно, такие последовательности не являются случайными. С другой стороны, 200-битовая последовательность, порождённая бросанием монеты, не может быть сжата, поскольку для этого процесса, вообще говоря, отсутствует закономерность в чередовании нулей и единиц; это совершенно случайная последовательность.

Из всех возможных последовательностей битов большинство несжимаемы и, следовательно, случайны. Поскольку последовательность битов можно рассматривать как представление по основанию 2 любого вещественного числа (если допускать бесконечные последовательности), отсюда вытекает, что большинство вещественных чисел на самом деле случайны. Нетрудно показать, что алгоритмически случайное число, такое, как Ω, проявляет обычные статистические свойства, связанные в нашем представлении со случайностью. Одним из таких свойств является нормальность: каждый возможный разряд появляется в числе с равной частотой. Если речь идёт о двоичном представлении, то при стремлении числа разрядов к бесконечности, нулей и единиц будет в точности по 50%.

Для того чтобы Ω имела смысл, должно выполняться одно техническое условие: программа на входе должна быть самоограничивающейся. Иными словами, информация о её общей длине (в битах) должна содержаться в самой программе. (Это на первый взгляд малозначительное условие, тормозившее прогресс в данной области в течение почти десятка лет, заставило переопределить понятие алгоритмической случайности.) Существующие языки программирования предназначены для построения самоограничивающихся программ, поскольку в этих языках предусмотрены механизмы начала и окончания программы. Такие конструкции позволяют программе содержать правильно определённые подпрограммы, которые в свою очередь могут включать в себя другие вложенные подпрограммы. Поскольку самоограничивающиеся программы строятся при помощи конкатенации (объединения двух последовательностей, скажем, строк или файлов, в одну. — Ред.) и вложения самоограничивающихся подпрограмм, программа синтаксически полна лишь тогда, когда последняя открытая подпрограмма «закрыта». По сути механизмы начала и окончания программ и подпрограмм функционируют соответственно как левая и правая скобка в математических выражениях.

Если бы программы не были самоограничивающимися, их нельзя было бы построить из подпрограмм, и суммирование вероятностей остановки для всех программ дало бы бесконечный результат. Если же вы рассматриваете лишь самоограничивающиеся программы, то Ω не только ограничена 0 и 1, но её можно явно вычислить «в пределе снизу». Другими словами, можно вычислять элементы бесконечной последовательности рациональных чисел (выраженных конечной последовательностью битов), каждое из которых ближе к точному значению Ω, чем предыдущее.

Один из способов сделать это — систематически вычислять Ω_n для возрастающих значений n; здесь Ω_n — вероятность того, что совершенно случайная программа длиной до n битов остановится через n секунд, если она выполняется на данном компьютере. Поскольку имеется 2^k возможных программ длиной k битов, Ω_n можно в принципе вычислить: для каждого значения k от 1 до n надо определить, сколько из этих возможных программ на самом деле останавливается через n секунд, умножить это число на 2^–k, а затем просуммировать все полученные произведения. Иначе говоря, каждая такая останавливающаяся k-битовая программа вносит свой вклад, равный 2^–k, в значение Ω; вклад программ, которые не останавливаются, равен 0.

Если бы мы каким-то чудом узнали значение Ω с k точными разрядами, мы могли бы вычислять последовательность Ω_n, пока не получили бы значение, равное данному значению Ω. Тогда мы бы нашли все останавливающиеся программы размером меньше k; это по существу означало бы, что решена поставленная Тьюрингом проблема остановки для всех программ размером меньше k битов. Конечно, для разумного значения k требуемое для вычисления время было бы огромным.

До сих пор при обсуждении проблемы остановки я обращался исключительно к её компьютерно-программной интерпретации, но в свете работы Дж. Джоунса из Университета в Калгари и Ю. В. Матиясевича из Ленинградского отделения Математического института им. Стеклова АН СССР в этой проблеме появляется новое «измерение». Исследования упомянутых авторов дают метод, позволяющий представить эту проблему в виде утверждений о диофантовых уравнениях определённого класса. Эти алгебраические уравнения, составленные при помощи операций над целыми числами — умножения, сложения и возведения в целую степень, названы по имени греческого математика Диофанта Александрийского, жившего в III веке н.э.

Выражаясь точнее, метод Джоунса и Матиясевича позволяет отождествить утверждение о том, что некоторая конкретная программа не остановится, с утверждением о том, что одно из уравнений из определённого класса диофантовых уравнений не имеет решений в целых числах. Как и в оригинальной версии проблемы остановки для компьютеров, здесь, если решение существует, это легко доказать: всё, что требуется, — это подставить правильные числа и проверить, равными ли получились левая и правая части уравнения. Доказать же несуществование решения (если оно действительно отсутствует) намного сложнее.

Класс уравнений строится исходя из базового уравнения, которое содержит конкретную переменную k, называемую параметром и принимающую значения 1, 2, 3 и т.д. (см. рисунок ниже). Таким образом, имеется бесконечно большой класс уравнений (по одному уравнению на каждое значение параметра k), которые можно получить из одного базового уравнения для каждой программы из «семейства» программ. Математическое утверждение о том, что диофантово уравнение с параметром k не имеет решения, равносильно утверждению, что k-я компьютерная программа никогда не остановится. С другой стороны, если k-я программа останавливается, то соответствующее уравнение имеет в точности одно решение. В некотором смысле истинность (или ложность) утверждений этого типа является математически неопределённой, поскольку она изменяется непредсказуемым образом, когда параметр k принимает различные значения.

«Класс» уравнений порождается путём придания параметру k базового уравнения различных целочисленных значений.

Мой подход к непредсказуемости в математике подобен этому, но он приводит к гораздо более высокой степени случайности. Вместо «арифметизации» компьютерных программ (которые могут или не могут останавливаться) как класса диофантовых уравнений, я применяю метод Джоунса и Матиясевича для арифметизации единственной программы вычисления k-го разряда Ω_n.

Этот метод основан на любопытном свойстве чётности биномиальных коэффициентов, которое было замечено Э. Люка сто лет назад, но до сих пор оставалось неоценённым по достоинству. Биномиальные коэффициенты представляют собой множители при степенях x^k в разложении выражений вида (x+1)ⁿ. Эти коэффициенты легко вычисляются с помощью так называемого треугольника Паскаля (см. рисунок ниже).

В теореме Люка утверждается, что коэффициент при x^k в разложении (x+1)ⁿ нечётен только тогда, когда каждый разряд в двоичном представлении числа k меньше или равен соответствующему разряду в двоичном представлении числа n (сопоставление начинается с правых элементов). Это можно выразить проще, сказав, что коэффициент при x^k в разложении (x+1)ⁿ нечётен, если для каждого разряда k, равного 1, соответствующий разряд n тоже равен 1; в противном случае коэффициент чётен. Например, коэффициент при x² в разложении бинома (x+1)⁴ равен 6, т.е. чётный. Соответственно единица в двоичном представлении двойки (10) не стоит на том же месте, что и единица в двоичном представлении четвёрки (100).

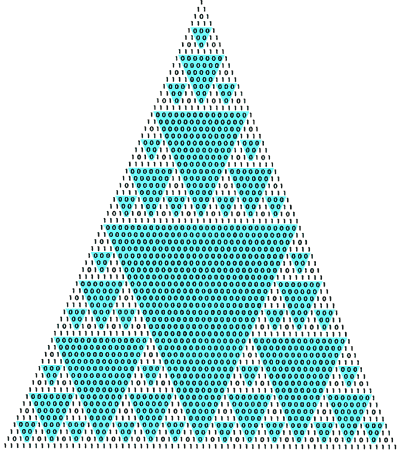Треугольник Паскаля (вверху) служит для вычисления коэффициентов разложения выражений вида (x+1)n. Начав с треугольника из единиц, вычисляют значения на каждом последовательном уровне путём сложения соседних чисел; последней ставят единицу. Таким образом можно определить, например, что (x + 1)4 = 1x4 + 4x3 + 6x2 + 4x + 1x0. Этот треугольник можно превратить в привлекательный фрактальный узор, если заменить нечётные коэффициенты единицами, а чётные — нулями (внизу). Узор демонстрирует свойство коэффициентов, применяемое при «арифметизации» компьютерных программ, которая преобразует их в алгебраические уравнения.

Хотя идея арифметизации проста и изящна, выполнение этого построения представляет собой громоздкую программистскую задачу. Тем не менее мне казалось, что это может быть интересным. Поэтому я разработал программу «компилятор» для получения уравнений из программ для «регистровой машины». Регистровая машина представляет собой компьютер, состоящий из небольшого множества регистров для хранения чисел произвольной величины. Разумеется, это абстракция, поскольку любой реальный компьютер имеет регистры ограниченного объёма.

Подав на вход реального компьютера, имеющего программу-компилятор, программу регистровой машины, которая выполняет инструкции на языке Лисп, получим через несколько минут на выходе уравнение длиной около 200 страниц, содержащее примерно 17 000 неотрицательных целых переменных. Итак, я могу вывести диофантово уравнение с параметром k, кодирующее k-й разряд Ω_n, путём простой подстановки программы на Лиспе (в двоичной форме), предназначенной для вычисления k-го разряда Ω_n, в 200-страничное уравнение. Для любой заданной пары значений k и n диофантово уравнение имеет в точности одно решение, если k-й разряд Ω_n равен 1, и не имеет решения, если k-й разряд Ω_n равен 0.

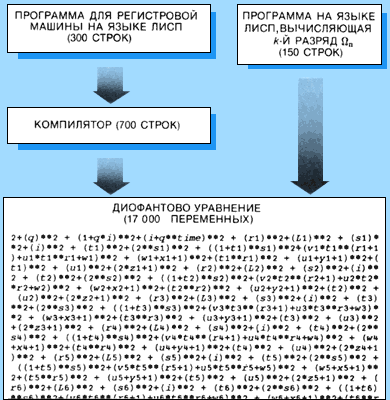Арифметизация Ω выполняется путём подстановки двоичного представления конкретной программы для вычисления k-го разряда Ωn (в двоичной форме) вместо переменной в уравнение, полученное из программы для универсального компьютера. Ωn является n-й аппроксимацией Ω — вероятности остановки компьютера при условии, что биты, составляющие его программу, определены случайным образом, например при помощи бросания монеты.

Поскольку это верно для любой пары значений k и n, можно, вообще говоря, зафиксировать k и систематически увеличивать значение n, вычисляя k-й разряд Ω_n для каждого значения n. Для малых значений n k-й разряд Ω_n будет беспорядочно флуктуировать между 0 и 1. В конце концов, однако, он станет равным 1 или 0, поскольку для очень больших значений n он должен быть равен k-му разряду Ω, который неизменен. Следовательно, диофантово уравнение в действительности имеет бесконечное число решений для конкретного значения своего параметра k, если k-й разряд Ω оказывается равным 1, и лишь конечное число решений, если k-й разряд Ω оказывается равным 0. Таким образом, вместо того чтобы выяснять, имеет ли диофантово уравнение решения для каждого значения своего параметра k, я узнаю, имеет ли оно бесконечно много решений.

На первый взгляд может показаться, что мы мало выигрываем, спрашивая «имеет ли уравнение бесконечно много решений», вместо «имеет ли оно вообще решения». Но на самом деле это очень важное различие: ответы на эти вопросы логически независимы. Два математических утверждения считаются логически независимыми, если одно нельзя вывести из другого, т.е. если ни одно из них не является логическим следствием другого. Это понятие независимости обычно отличают от понятия независимости, используемого в статистике. Последнее заключается в том, что два случайных события называются независимыми, если исход одного из них не оказывает влияния на исход другого. Например, результат бросания монеты никоим образом не влияет на результат следующего бросания: эти результаты статистически независимы.

Я использую оба понятия независимости. Ответ на мой вопрос для одного значения k логически независим от ответа на этот вопрос для другого значения k. Причина заключается в том, что конкретные разряды Ω, определяющие ответ, независимы статистически.

Легко доказать, что примерно для половины значений k число решений конечно, а для другой половины число решений бесконечно, однако не существует способа «сжать» эти ответы в формулу или набор правил: они как бы «подражают» результатам бросания монеты. Поскольку Ω алгоритмически случайна, то даже знание ответов для 1000 значений k не поможет найти правильный ответ для 1001-го значения k. Устанавливая, имеет ли конкретное уравнение конечное или бесконечное число решений, математик находится в положении игрока, бросающего монету. Какие бы аксиомы и доказательства мы ни применяли для диофантова уравнения с одним значением k, они будут неприменимы для того же самого уравнения при другом значении k.

Математическое рассуждение оказывается в этом случае в принципе бесполезным, поскольку нет логических взаимосвязей между полученными таким способом диофантовыми уравнениями. Будь ты хоть семи пядей во лбу, выведи длиннейшее доказательство, используй сложнейшие математические аксиомы, построенный бесконечный ряд предложений, устанавливающий, конечно или бесконечно число решений диофантова уравнения, окажется бесполезным, если k увеличить. Итак, даже в элементарных разделах теории чисел, связанных с диофантовыми уравнениями, возникают случайность, неопределённость и непредсказуемость.

Но каким же образом теорема Гёделя о неполноте, проблема остановки Тьюринга и моя работа влияют на математику? Большинство математиков не обращают внимания на эти результаты. Конечно, в принципе они согласны, что любая конечная система аксиом неполна, но на практике они игнорируют этот факт, как непосредственно не относящийся к их работе. Но иногда, к сожалению, его нельзя игнорировать. Хотя в исходном виде теорема Гёделя казалась применимой лишь к необычным математическим предложениям, не имеющим практического интереса, алгоритмическая теория информации показала, что неполнота и случайность являются естественными и распространёнными повсюду свойствами. Это подсказывает мне, что следует более серьёзно относиться к возможности поиска новых аксиом относительно целых чисел.

Тот факт, что многие математические проблемы оставались веками и даже тысячелетиями нерешёнными, похоже, подтверждает мою точку зрения. Математики непоколебимо стоят на том, что причина неудач в решении подобных проблем заключена только в самих проблемах, но не заключается ли она в неполноте системы их аксиом? Например, вопрос о том, существуют ли нечётные совершенные числа, не поддаётся решению со времён древних греков. (Совершенным называется число, равное сумме своих делителей, исключая само это число. Например, 6 — совершенное число, поскольку 6=1+2+3.) Не может ли быть так, что утверждение «Не существует нечётных совершенных чисел» недоказуемо? Если это так, то не лучше ли принять его за аксиому?

Большинству математиков это предположение может показаться смехотворным, но для физика или биолога оно не выглядит столь уж абсурдным. Для тех, кто работает в эмпирических областях науки, основным критерием, позволяющим судить о том, следует ли рассматривать некоторое суждение как основание теории, служит полезность этого суждения, а вовсе не обязательно его «самоочевидная истинность». Если имеется много догадок, которые можно обосновать обращением к некоторой гипотезе, учёные-эмпирики принимают эту гипотезу. (Из несуществования нечётных совершенных чисел, по-видимому, не следует важных выводов, и, согласно этому критерию, такая аксиома не является полезной.)

На самом деле в некоторых случаях математики в своей работе опираются на недоказанные, но полезные предположения. Например, так называемая гипотеза Римана, хотя она никогда не была доказана, часто считается верной, потому что на ней основано много важных теорем. Более того, эта гипотеза была эмпирически проверена с помощью самых мощных компьютеров, и ни один опровергающий её пример не был найден. Компьютерные программы (которые, как я уже сказал, эквивалентны математическим утверждениям) проверяются таким же способом — тестированием некоторого числа вариантов, а не строгим математическим доказательством.

Существуют ли проблемы в других областях науки, для решения которых был бы полезен этот экскурс в основания математики? Я думаю, алгоритмическая теория информации может применяться в биологии. Регуляторные гены развивающегося зародыша являются по существу вычислительной программой построения организма. «Сложность» этой биохимической компьютерной программы можно, как мне думается, определить в терминах, аналогичных тем, что я развил при квантификации информационного содержания Ω.

Хотя Ω совершенно случайна (или бесконечно сложна) и никогда не может быть вычислена точно, её можно аппроксимировать с произвольной точностью, если в распоряжении имеется бесконечный отрезок времени. Мне кажется, что «сложность» живого организма может быть приближена таким же образом. Последовательность Ω_n, аппроксимирующую Ω, можно рассматривать как метафору эволюции, и, возможно, она содержит зерно математической модели, описывающей эволюцию «сложности» биологического организма.

В конце своей жизни Дж. фон Нейман призвал математиков заняться созданием абстрактной математической теории происхождения и эволюции жизни. Эта фундаментальная проблема, подобно большинству проблем такого масштаба, бесконечно трудна. Возможно, алгоритмическая теория информации позволит найти путь, по которому следует идти.