С. 74–88

К данной публикации непосредственно примыкает ещё пара материалов популярного толка: 1) статья о гипотезе Пуанкаре и её доказательстве Перельманом и 2) видеоролик о форме пространства. Статья Грэхема Коллинза «Форма пространства» опубликована в октябрьском номере журнала «В мире науки» за 2004 год и её легко найти. Видеоролик «The Shape of Space» найти сложнее, поэтому я решил выложить его сам, чтобы не утруждать интересующихся его поиском. — E.G.A.

Математика трёхмерных многообразий



Изучение топологии трёхмерных аналогов поверхностей наводит на мысль, что Вселенная, возможно, изогнута подобно запутанной верёвочной петле. Сейчас становится ясно, что большинство трёхмерных многообразий можно изучить геометрическими методами

УИЛЬЯМ П. ТЁРСТОН,   ДЖЕФФРИ Р. УИКС

Тысячи лет назад люди думали, что Земля плоская. Это должно было казаться совершенно очевидным любому наблюдателю в океане или прерии; обсуждался не лишённый смысла вопрос, бесконечна ли Земля или у неё есть край. Сейчас понятно, как могло возникнуть такое в корне ошибочное представление: даже с высоты нескольких тысяч метров небольшая часть земной поверхности, имеющей приближённо сферическую форму, выглядит как небольшой участок плоскости. Реже отдают себе отчёт в том, что бесчисленное количество других форм земной поверхности при локальном наблюдении выглядело бы точно так же. Например, если исходить из таких локальных наблюдений, Земля могла бы иметь форму неправильной капли или бублика.

Исследования в той области математики, которая называется топологией, объясняют, что с такой же ситуацией мы сталкиваемся при попытках описать форму Вселенной в целом на основании наблюдений ограниченной её части, видимой из нашей точки пространства. Наблюдатель, находящийся на Земле, не может с уверенностью сделать вывод, что Вселенная на всём бесконечном протяжении сохраняет геометрическую структуру обычного евклидова пространства, хотя до сих пор нет оснований и для противоположного утверждения. Если же геометрия Вселенной не является евклидовой, то каковы альтернативы? Одна хорошо известная идея состоит в том, что пространство «искривлено» почти таким же образом, как может быть искривлена поверхность. Трёхмерная кривизна пространства и тесно связанная с ней четырёхмерная кривизна пространства-времени стали важными понятиями в астрономии и космологии, поскольку они играют ключевую роль в общей теории относительности Эйнштейна.

Тем не менее определение одной только кривизны не достаточно для описания того, что мы называем формой Вселенной. Некоторые возможные типы трёхмерной структуры Вселенной можно описать по аналогии с двумерными поверхностями, но эта аналогия лишь наводит на мысль о богатстве и разнообразии форм, появляющихся при добавлении третьего измерения. В действительности, поскольку пространство и время в теории относительности рассматриваются как единое целое, называемое пространством-временем, можно предположить, что адекватное математическое описание Вселенной должно быть четырёхмерным. Однако есть основания надеяться, что структура четырёхмерного пространства-времени определяется структурой его трёхмерной пространственной части. Поэтому, чтобы без предубеждения изучать структуру Вселенной в целом, нужно начать с изучения типов трёхмерных объектов, геометрические свойства которых могли бы находиться в согласии со свойствами наблюдаемой Вселенной. Такие объекты называются трёхмерными многообразиями или 3-многообразиями.

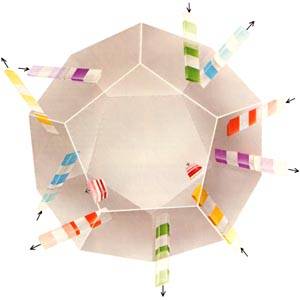Рис. 1. Топологическая структура Вселенной не обязана совпадать со структурой бесконечного трёхмерного евклидова пространства. Математическая теория трёхмерных многообразий показывает, что пространство может «искривляться само в себе» бесконечным числом способов. Одной из возможных моделей топологии пространства служит трёхмерное многообразие, открытое Г. Зейфертом и К. Вебером в 1932 году. Такое многообразие нельзя наглядно изобразить «извне», потому что для этого пришлось бы «взглянуть» на него из четвёртого или более высокого измерения. Тем не менее его можно мысленно представить себе как додекаэдр, противоположные грани которого математически склеены друг с другом, т.е. отождествлены. Раскрашенные планки, движущиеся сквозь грани додекаэдра внутрь и наружу, показывают, как склеивать грани: одна грань из каждой пары противоположных граней поворачивается вокруг оси, перпендикулярной её плоскости, на 1/10 полного оборота, а затем склеивается с противоположной гранью. Хотя на рисунке некоторые планки показаны снаружи додекаэдра, это только «призраки» (поскольку считается, что всё пространство состоит лишь из внутренних точек додекаэдра). Когда одна из планок выдвигается наружу, её выступающая часть исчезает, одновременно как бы входя внутрь додекаэдра сквозь противоположную грань. Если Вселенная устроена как многообразие Зейферта–Вебера, то она конечна, но будет расширяться вечно.

Изучение 3-многообразий в некотором смысле обобщает изучение 2-многообразий, или поверхностей. Но если описание и классификация всех 2-многообразий известны топологам уже более ста лет, то систематическая классификация всех 3-многообразий до сих пор остаётся нерешённой проблемой ввиду чрезвычайной сложности форм некоторых из них. Меру сложности многообразия подсказывает математическая процедура, называемая хирургией. Хирургия позволяет построить 3-многообразие по любой спутанной верёвочной петле независимо от того, насколько она заузлена. Представим себе, что сравниваются два спутанных мотка ниток или рыболовной лески, и нужно узнать, в точности ли одинаковым способом они перепутаны. Если нет способа систематической классификации таких запутанных мотков, то нет надежды и на успех в изучении 3-многообразий. Поэтому до недавнего времени математики имели мало оснований считать, что можно построить систематическую теорию 3-многообразий.

Сейчас такое пессимистическое заключение следует пересмотреть. Исследования одного из нас (Тёрстона) по геометрии 3-многообразий показывают, что существует схема, которая может привести к пониманию структуры всевозможных 3-многообразий. Все известные 3-многообразия укладываются в эту схему, и в результате удаётся описать в геометрических терминах их скручивание и изгибание.

Теория многообразий возникла в XIX веке в связи с потребностью геометрической интерпретации количественных соотношений. Например, множество решений уравнения с двумя неизвестными можно изобразить как некоторое множество точек на плоскости. Каждая точка отвечает паре значений неизвестных, удовлетворяющих данному уравнению; в типичных случаях это множество точек представляет собой кривую или несколько кривых. Подобно этому, множество решений уравнения с тремя неизвестными обычно можно изобразить в виде двумерной поверхности в трёхмерном пространстве, например, такой, как поверхность сферы. Для уравнений более чем с тремя неизвестными множество решений можно геометрически описать таким же образом: это многообразие более высокой размерности, лежащее в пространстве ещё большего числа измерений. Хотя такие объекты наглядно представить нельзя, математики разработали качественные методы для исследования уравнений, приводящих к многообразиям высокой размерности.

В действительности топология не в состоянии решать уравнения. Зато она предоставляет математический словарь: прилагательные и существительные, с помощью которых можно описывать общие свойства множества решений без его фактического определения. Так, хотя многообразие точек, изображающих решения какого-то уравнения, имеет вполне определённую форму, предметом изучения топологии являются не свойства этой конкретной формы, а только те свойства, которые сохраняются при любых деформациях этого многообразия, выполняемых без разрезов, разрывов или проколов.

Бублик можно превратить в кофейную чашку, если сделать вмятину на его поверхности, а затем увеличивать эту вмятину, одновременно сжимая остальную часть бублика. Согласно старой шутке, тополог — это человек, который не отличает бублик от кофейной чашки (с ручкой). Однако тополог наверняка отличит поверхность бублика от поверхности стакана без ручек, поскольку ни одну из них нельзя непрерывно деформировать в другую. Может показаться, что, допуская произвольные деформации, топология отбрасывает самые интересные свойства многообразия. Однако во многих математических вопросах топологическая информация играет важную роль.

Первые существенные продвижения в топологической теории 3-многообразий были сделаны на рубеже XIX и XX веков в работах Анри Пуанкаре, Макса Дена и Пауля Хегора. Одна из трудностей при изучении трёхмерных многообразий состоит в том, что непосредственно-наглядные образы частично должны уступить место абстрактным представлениям. Многие поверхности нетрудно представить себе, поскольку на них можно взглянуть снаружи, из третьего измерения: размерность объемлющего пространства на единицу больше размерности поверхности. Дополнительное измерение оставляет поверхности достаточно свободы для изгибания и смыкания с самой собой. Можно было бы попытаться взглянуть и на трёхмерные многообразия со стороны, как бы из четвёртого измерения, но оказывается, что в таких акробатических трюках нет необходимости.

В XIX веке математики открыли, что любое двумерное многообразие можно представить как многоугольник, стороны которого определённым образом склеены или, иными словами, отождествлены друг с другом. В романе «Флатландия», опубликованном в 1884 году, Э. Эббот описывает двумерное существо, постоянно живущее на двумерном многообразии с более экзотической топологией — на квадрате, противоположные стороны которого отождествлены. Когда флатландец пересекает верхнюю сторону квадрата, он вновь появляется на нижней его стороне; если он уходит вправо, то появляется слева. Поэтому, по сути дела, верх квадрата приклеен к его низу, а правая сторона — к левой. Стоит отметить, что так же устроены многие видеоигры: когда фигура уходит за верхний край экрана, она появляется снизу, и т.д.

Для квадрата склеивание выполнить просто. Соединение верхней и нижней сторон даёт цилиндр, открытый с обоих торцов; склеивание открытых торцов даёт бублик. После склеивания сторон «швы» исчезают; флатландец не может определить, где было произведено склеивание. Бублик и квадрат с надлежащим образом отождествлёнными сторонами считаются топологически одним и тем же абстрактным многообразием, а именно двумерным тором.

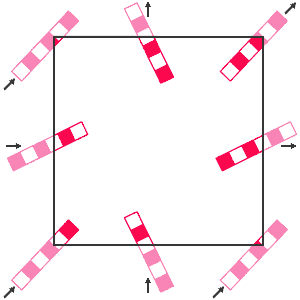Рис. 2. Двумерное многообразие, называемое двумерным тором, можно представить в виде квадрата, противоположные стороны которого абстрактно склеены друг с другом: верхняя сторона отождествлена с нижней, а правая — с левой. Если размеченная планка выдвигается наружу сквозь правую сторону, она появляется снова с левой стороны; если планка уходит за верхнюю сторону, то она появляется снизу. Все вершины квадрата склеиваются в одну точку многообразия.

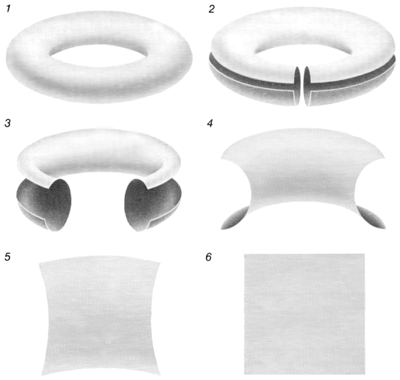Рис. 3. Поверхность бублика с одной дыркой можно разрезать и развернуть так, что получится квадрат. Если противоположные стороны квадрата абстрактно склеены, то полученная поверхность топологически эквивалентна бублику. Так как квадрат плоский, его геометрия евклидова. Поэтому говорят, что с топологической точки зрения поверхность бублика с одной дыркой допускает евклидову геометрию.

Однако, как показывают видеоигры, для интуитивного понимания двумерного тора не обязательно производить реальное склеивание. Немного потренировавшись, можно с легкостью уследить за движением объекта по квадрату, для которого склеивание только подразумевается. Абстрактное склеивание вводит в круг геометрической интуиции многие многообразия, которые иначе трудно было бы себе представить. И вот что для нас особенно важно: трюк со склеиванием легко обобщается и позволяет для понимания структуры 3-многообразий привлечь геометрическую интуицию.

Рассмотрим трёхмерное многообразие, которое порождается прямоугольным блоком пространства, например внутренней частью комнаты. Склеим условно переднюю стену комнаты с задней, левую стену с правой, а потолок с полом. Если бы склеивание было сделано на самом деле, то пришлось бы вообразить, что комната изгибается и соединяется сама с собой в четвёртом измерении. Однако всё, что нужно для описания этого многообразия, определяется процедурой абстрактного склеивания. Если объект внутри многообразия движется к передней стене, он исчезает на ней и появляется на задней стене; точно так же, когда объект исчезает на правой стене, он появляется на левой и исчезает на потолке, когда появляется на полу. Это движение очень похоже на движение по двумерному тору; полученное многообразие — трёхмерный аналог двумерного тора и поэтому называется трёхмерным тором.

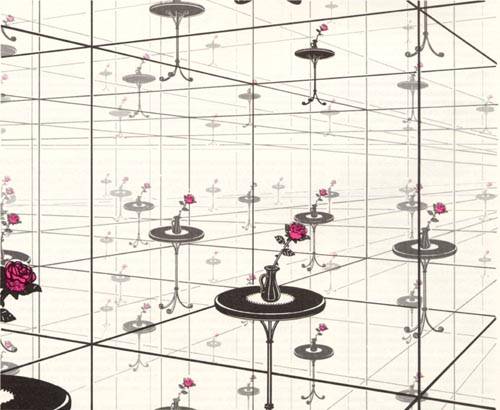Рис. 4. Вид, открывающийся наблюдателю внутри трёхмерного тора, похож на то, что можно увидеть в комнате, все стены, пол и потолок которой зеркальны; только изображение, в отличие от обычного зеркального отражения, не перевёрнуто. Луч зрения уходит, скажем, сквозь правую стену и возвращается из левой стены; поэтому, глядя направо, наблюдатель видит комнату так, как будто он смотрит на неё снаружи сквозь прозрачную левую стену (только при этом он видит в комнате своего двойника). Аналогичные картины возникают при взгляде вперёд или вверх. Так как луч зрения при продолжении неограниченно пронизывает трёхмерный тор, комната будет выглядеть как простирающаяся во все стороны бесконечная прямоугольная решётка. Но трёхмерный тор не бесконечен, поскольку все видимые образы, составляющие бесконечную прямоугольную пространственную решётку, — изображения одного и того же предмета.

Отвлекаясь от обычных представлений о пространстве и физической реальности, можно легко вообразить «жизнь» в трёхмерном торе. Если смотреть на заднюю стену, то луч зрения проходит сквозь эту стену и возвращается из противоположной точки передней стены; вы видите свою копию «анфас». Посмотрите вправо — и увидите свою копию слева, посмотрите вниз на пол — увидите макушку своей головы. Поскольку лучи зрения при продолжении пересекают комнату во всех направлениях множество раз, вы видите, что возникает бесконечное число ваших копий и копий комнаты; все они расположены в виде прямоугольной пространственной решётки. Оптический эффект подобен тому, который возникает в комнате, все стены, пол и потолок которой зеркальны. Разница в том, что «отражения» не перевёрнуты, а в точности повторяют оригинал.

Астрономы не обнаружили таких своеобразных оптических эффектов; следует ли из этого, что Вселенная не может быть трёхмерным тором? Нет. Возраст Вселенной находится примерно между 10 и 20 млрд. лет. Если бы она была трёхмерным тором, например, порядка 60 млрд. световых лет в поперечнике, то свет ещё не успел бы сделать полный оборот. Другая возможность состоит в том, что наблюдательная астрономия уже зарегистрировала свет, который проделал полный путь вокруг Вселенной: если Вселенная — трёхмерный тор, то одна из дальних галактик, которые мы наблюдаем, может быть нашей собственной. Это трудно было бы проверить, поскольку изображение нашей Галактики сформировано световыми лучами, покинувшими источники света миллиарды лет назад и потратившими это время на пересечение Вселенной. Имея неограниченную разрешающую способность зрения, мы могли бы увидеть Млечный Путь на ранних этапах его эволюции, в момент испускания света. Такая Вселенная имеет конечный обьём, но не имеет никакой границы.

Подобные модели возможной пространственной структуры Вселенной можно получить, пользуясь вместо куба другими многогранниками. Во всех случаях лучший способ понять устройство многообразия — это вообразить, что определённые грани многогранника абстрактно склеены друг с другом. Два таких многообразия легко получить из правильного додекаэдра. 12 граней додекаэдра — правильные пятиугольники; их можно разбить на 6 пар параллельных между собой диаметрально противоположных граней.

Первое трёхмерное додекаэдральное многообразие получается так: один из пятиугольников каждой пары поворачивается на 1/10 полного оборота против часовой стрелки вокруг оси, перпендикулярной его плоскости, после чего отождествляется со вторым (противоположным ему) пятиугольником. Это многообразие называется многообразием Пуанкаре, потому что оно эквивалентно трёхмерному многообразию, открытому Пуанкаре в 1902 году. (Однако Пуанкаре не знал, что это многообразие можно получить из додекаэдра.) Второе додекаэдральное многообразие получается склеиванием каждого пятиугольника с противоположным, предварительно повернутым на 3/10 полного оборота против часовой стрелки вокруг оси, перпендикулярной его плоскости. Это многообразие называется додекаэдральным многообразием (или пространством) Зейферта–Вебера в честь Г. Зейферта и К. Вебера (работающего сейчас в Женевском университете); они открыли это многообразие в 1932 году (см. рис. 1). Как и трёхмерный тор, оба многообразия дают модели Вселенной конечного объёма, но без границы или края.

Подобным образом можно получить множество различных моделей крупномасштабной структуры пространства. Поскольку большинство многогранников неправильные, большинство трёхмерных многообразий приходится склеивать из них. Если число граней велико, то описание склеивания, как правило, сильно усложняется.

Может показаться, что в таких занятиях есть нечто нереальное. Неспециалист, вероятно, согласится, что истинная топология пространства — достойный объект для размышлений; но его, наверное, удивило бы, как далеко заводят эти размышления. В частности, он мог бы усомниться в целесообразности изучения «пространств» во множественном числе. С точки зрения тополога, такая критика «бьёт мимо цели», поскольку она направлена только на образно-описательную часть топологии. Конечно, занятия топологией можно оправдать её применениями к задачам, возникающим в совсем других ситуациях, но и сама по себе топология — это теория чистых геометрических форм, а не теория реального мира. Если бы завтра структура пространства каким-нибудь образом стала известна, никто из топологов не отказался бы от изучения абстрактных пространств.

Это утверждение никоим образом не означает, что топология не имеет отношения к реальному миру. Наоборот, как и другие области математики, топология имеет многочисленные прочные связи с действительностью, но эти связи не прямые. Если некоторые конкретные образные представления (например, пространственные) становятся неубедительными, то лучше отбросить эти представления, чем отказаться от изучения порождённых ими математических объектов. Опыт вновь и вновь показывает, что математическая теория с богатой внутренней структурой обычно приводит к выводам, важным для понимания реального мира, причём часто такими путями, которые никак нельзя было предвидеть до её развития. Никакая теория никогда не достигла бы той степени зрелости, на которой только и возникают такие приложения, если бы она была постоянно обременена уже отжившими образными представлениями.

Чтобы убедиться, насколько широк диапазон топологических исследований, полезно на время покинуть область космологии и перейти к более земным вопросам. Рассмотрим механическую систему (шарнирный механизм), состоящую из стержней и шарниров, подобную системе, которая связывает между собой клавишу и печатающий элемент в пишущей машинке. Мы будем рассматривать только плоские шарнирные механизмы, или, иными словами, системы твёрдых стержней, скреплённых друг с другом таким образом, что все стержни могут двигаться лишь в одной плоскости. При этом хотя бы в одной точке система должна быть прикреплена к плоскости; эту точку назовём базовой.

Задача теории шарнирных механизмов — анализ возможных их движений. Существует много реальных механических устройств, к которым применимо такое исследование, причём они могут и не иметь внешнего сходства с системой соединённых между собой стержней. Изучение шарнирных механизмов было очень популярно во второй половине XIX века, когда интересовались задачей построения таких шарнирных механизмов, в которых хотя бы одна точка двигалась по прямой линии. Казалось, что решение этой задачи могло бы иметь много практических применений, например при конструировании двигателей для паровозов. Однако несмотря на то, что было найдено много элегантных теоретических решений этой задачи, ни одно из них не было применено на практике.

Шарнирный механизм математически представляется системой прямолинейных отрезков на плоскости; в некоторых точках пересечения отрезков могут быть установлены оси для шарниров. В математической теории считается, что отрезки и оси шарниров могут свободно проходить друг сквозь друга. Не так легко построить физическую модель, стержни и шарниры которой повторяют движения идеального шарнирного механизма, но для математической теории это несущественно. Оказывается, что для любого «математического» шарнирного механизма существует реальный механизм, выполняющий те же движения; однако соответствующая физическая система может быть устроена значительно сложнее своего теоретического эквивалента и выглядеть совершенно иначе.

Множество всех возможных состояний шарнирного механизма называется его конфигурационным пространством; в большинстве случаев оно является топологическим многообразием. Рассмотрим простейший шарнирный механизм, состоящий из единственного стержня, один конец которого шарнирно закреплён в базовой точке плоскости, а другой может свободно двигаться в этой плоскости. Подвижный конец стержня описывает окружность на плоскости, и каждой точке этой окружности соответствует единственное состояние системы. Конфигурационное пространство есть окружность, которую можно иначе рассматривать как прямолинейный отрезок, концы которого абстрактно склеены друг с другом. Окружность является одномерным многообразием, аналогичным двумерному тору; каждая точка этого многообразия отождествляется с единственным положением рассмотренного шарнирного механизма.

Присоединив другой стержень к концу первого, мы получим двузвенный кривошип — шарнирный механизм с двумя степенями свободы. Если второй стержень короче первого, то его свободный конец может попасть в любую точку кольца с центром в базовой точке. Это кольцо снаружи ограничено окружностью, радиус которой равен сумме длин обоих стержней, а изнутри — окружностью, радиус которой равен разности их длин. Если стержни имеют одинаковую длину, то свободный конец второго стержня может находиться в любой точке круга, радиус которого равен сумме длин стержней. Если же второй стержень длиннее первого, то возможные положения его свободного конца снова заполняют кольцо, внутренний радиус которого равен разности длин стержней. Однако не следует принимать эти множества точек за конфигурационное пространство шарнирного механизма. Причина различия между ними состоит в том, что положение конца второго стержня ещё не полностью определяет конфигурацию системы. Для каждого положения свободного конца второго стержня колено нашего двузвенного кривошипа может быть выгнуто в ту или другую сторону.

Чтобы правильно описать конфигурационное пространство, проще рассматривать возможные конфигурации всего двойного кривошипа, не обращая внимания на положение его свободного конца. Каждая конфигурация может быть задана двумя углами, а именно углами между каждым из стержней и некоторым фиксированным направлением (скажем, направлением вправо); углы отсчитываются против часовой стрелки. Эти два угла независимо друг от друга принимают все значения от 0° до 360°, но для каждого стержня углы 0° и 360° отождествляются. Будем откладывать эти углы на взаимно перпендикулярных координатных осях плоскости; тогда каждая точка квадрата, ограниченного прямыми линиями, отвечающими значениям 0° и 360° каждого из углов, изображает определённую конфигурацию двойного кривошипа. Кроме того, каждой конфигурации системы соответствует некоторая точка этого квадрата. Поскольку углы 0° и 360° отождествляются, верхняя сторона квадрата отождествляется с нижней, а левая — с правой. Итак, конфигурационное пространство является двумерным тором.

Если присоединить к свободному концу двузвенного кривошипа третий стержень, то любое положение полученного трёхзвенного кривошипа можно описать, задав три угла, которые образуют его стержни с фиксированным направлением. Углы снова отсчитываются против часовой стрелки и пробегают значения от 0° до 360°. Как и прежде, углы 0° и 360° отождествляются. Если величины трёх углов отложить на трёх взаимно перпендикулярных координатных осях, то любое возможное положение трёхзвенного кривошипа будет представлено единственной точкой куба, противоположные грани которого абстрактно склеены друг с другом. Таким образом, конфигурационное пространство трёхзвенного кривошипа эквивалентно трёхмерному тору.

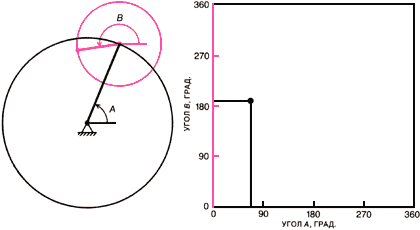Рис. 5. Двузвенный кривошип состоит из двух твёрдых стержней, соединённых между собой шарниром; конец одного стержня шарнирно закреплён. Стержни могут свободно вращаться вокруг шарниров, оставаясь в плоскости изображения (слева). Каждая возможная конфигурация двух стержней может быть задана точкой на плоскости, на которой введена прямоугольная система координат. Множество всех точек этой плоскости, отвечающих всевозможным конфигурациям шарнирного механизма, называется его конфигурационным пространством (справа). Поскольку при повороте любого из стержней на 360° конфигурация механизма не меняется, его конфигурационное пространство — это квадрат, стороны которого отвечают значениям 0° и 360° каждого из углов. Соответствующие точки противоположных сторон квадрата представляют одинаковые конфигурации механизма, т.е. конфигурационное пространство является двумерным тором.

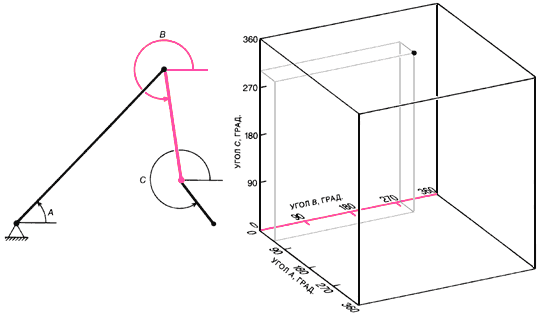Рис. 6. Трёхмерное многообразие, аналогичное двумерному тору, возникает как конфигурационное пространство плоского трёхзвенного кривошипа (слева). Если углы, образованные каждым стержнем с фиксированным направлением, отложить на трёх взаимно перпендикулярных осях, то любое возможное положение трёхзвенного кривошипа можно изобразить точкой куба (справа). При полном обороте какого-нибудь стержня конфигурация механизма не изменяется. Таким образом, в конфигурационном пространстве каждая грань куба, отвечающая повороту стержня на 360°, абстрактно отождествляется с противоположной гранью, отвечающей повороту того же стержня на нулевой угол. Полученное трёхмерное многообразие называется трёхмерным тором.

Все рассмотренные до сих пор конфигурационные пространства сводились к многоугольникам или многогранникам, стороны или грани которых можно было склеить без искажения их размеров и формы. Но никакие топологические правила не запрещают склеивать стороны или поверхности, геометрически не конгруэнтные. То, что в приведённых нами примерах склеивание частей происходило без искажений, объясняется лишь весьма частным характером этих примеров. Рассмотрим шарнирный механизм, состоящий из трёх двузвенных кривошипов; пусть каждый из них шарнирно прикреплён к одной из вершин равностороннего треугольника, а все свободные концы скреплены между собой одним центральным шарниром (см. рис. 8). Для изучения конфигурационного пространства этой системы сначала построим множество возможных положений центрального шарнира. Свободный конец каждого двузвенного кривошипа должен находиться в кольце с центром в соответствующей базовой точке. Поэтому центральный шарнир может попасть в любую точку, лежащую в пересечении трёх колец, отвечающих трём двузвенным кривошипам. Это пересечение представляет собой плоский криволинейный шестиугольник.

Рис. 7. Шарнирному механизму, состоящему из трёх двузвенных кривошипов, присоединённых свободными концами к центральному шарниру, тоже отвечает двумерное конфигурационное многообразие. Движение происходит в плоскости, и центральный шарнир может находиться в любой точке криволинейного шестиугольника.

Однако для построения конфигурационного пространства ещё не достаточно этого шестиугольника. Вспомним, что каждому положению свободного конца двузвенного кривошипа отвечают две различные конфигурации. Точно так же для любой точки шестиугольника колено каждого из трёх двузвенных кривошипов может быть выгнуто в одну из двух сторон. Тем самым общее число конфигураций системы трёх двузвенных кривошипов при фиксированном внутри шестиугольника положении центрального шарнира равно 2³, т.е. 8. Поэтому конфигурационное пространство описанной системы может быть построено из восьми криволинейных шестиугольников с помощью подходящего абстрактного склеивания их сторон.

Как же должны быть склеены эти восемь шестиугольников, чтобы получилось конфигурационное пространство? Если центральный шарнир системы трёх двузвенных кривошипов находится на стороне плоского шестиугольника, то оба стержня одного из этих кривошипов непременно должны лечь на одну прямую. Такое выпрямление может произойти двумя способами: стержни двузвенного кривошипа могут быть направлены либо одинаково, либо противоположно. Однако в обоих случаях конфигурация всего шарнирного механизма однозначно определена, как только заданы положение центрального шарнира и направления, в которых выгнуты колена двух других двузвенных кривошипов.

Каждой их тех двух сторон плоского шестиугольника, по которым может двигаться центральный шарнир, когда первый двузвенный кривошип выпрямлен, в конфигурационном пространстве отвечает не 8, а лишь 2² = 4 различных рёбер. Вдоль каждого такого ребра в конфигурационном пространстве склеиваются два шестиугольника. Эти два шестиугольника отвечают двум различным направлениям выгиба колена двузвенного кривошипа. Противоположная сторона первого шестиугольника в конфигурационном пространстве также склеивается с противоположной стороной второго шестиугольника, ибо при расположении на ней центрального шарнира первый двузвенный кривошип тоже выпрямляется. Направления выгиба двух других двузвенных кривошипов не меняются при переходе от первого ко второму шестиугольнику. Точно такие же рассуждения применимы ко всем другим рёбрам конфигурационного пространства.

Если центральный шарнир нашего механизма находится в вершине плоского шестиугольника, то два из двузвенных кривошипов должны выпрямиться. Поэтому в конфигурационном пространстве каждой вершине плоского шестиугольника соответствуют две точки вместо восьми — по одной на каждый из двух способов изгиба третьего двузвенного кривошипа. Четыре абстрактных шестиугольника, отвечающие четырём способам, которыми могут выгнуться два двузвенных кривошипа при сдвиге центрального шарнира из вершины внутрь плоского шестиугольника, имеют в конфигурационном пространстве общую вершину.

Конфигурационное пространство является поверхностью, которая в отличие от плоского шестиугольника не имеет ни углов, ни границы. Эту поверхность можно разбить на восемь шестиугольников. При этом получаются 6 × 2² = 24 ребра, по которым части примыкают друг к другу, и 6 × 2 = 12 вершин, в которых сходятся по четыре части.

Описание конфигурационного пространства системы трёх двузвенных кривошипов, которое мы привели выше, логически полно, поскольку определены все абстрактные отождествления. Тем не менее гораздо удобнее произвести реальные склеивания и построить полученное многообразие как замкнутую поверхность в пространстве. Оказывается, такое построение всегда осуществимо, если абстрактное склеивание приводит к многообразию, удовлетворяющему одному техническому условию, называемому ориентируемостью. Многообразие, которое мы описали выше, ориентируемо; поэтому склеивание можно произвести, но это не так просто.

В середине XIX века было доказано, что любое ориентируемое двумерное многообразие топологически эквивалентно поверхности кренделя с некоторым числом дырок. (Такую поверхность называют также сферой с ручками (или дырками). — Прим. перев.) Число дырок называется родом поверхности. Например, поверхность сферы имеет род 0. Род поверхности кофейной чашки с ручкой, так же как и поверхности бублика, равен 1. Род поверхности кренделя зависит от мастерства кондитера.

Для любой поверхности, разбитой на многоугольные клетки произвольной формы, число этих клеток минус число рёбер плюс число вершин есть константа, зависящая только от поверхности. Замечательно, что эта константа не зависит от способа разбиения поверхности на многоугольные клетки; она называется эйлеровой характеристикой поверхности в честь великого математика Леонарда Эйлера. Эйлерова характеристика поверхности рода n равна 2–2n. Так как поверхность может быть искривлена в пространстве, то многоугольники не обязаны быть плоскими, а их стороны могут быть почти произвольными кривыми. Например, сферу можно разбить на восемь треугольников, соединив северный и южный полюсы с четырьмя точками на экваторе. Так как в сфере нет дырок, то её род равен 0, а эйлерова характеристика должна равняться 2–2×0, т.е. 2. Легко проверить, что при нашем разбиении на поверхности сферы 6 вершин и 12 рёбер, так что эйлерова характеристика сферы, разбитой на 8 треугольников, и в самом деле равна 2. Стоит отметить, что количества граней, рёбер и вершин в этом примере отвечают правильному октаэдру, топологически эквивалентному сфере.

Так как конфигурационное пространство системы трёх двузвенных кривошипов можно разбить на 8 шестиугольных граней с 24 рёбрами и 12 вершинами, эйлерова характеристика этого пространства равна 8 – 24 + 12 = –4. Род n этого многообразия можно вычислить, приравнивая выражение 2–2n для эйлеровой характеристики найденному её значению –4. Отсюда следует, что n=3. Итак, восемь шестиугольников конфигурационного пространства рассмотренного шарнирного механизма можно с соблюдением правил склейки расположить на поверхности кренделя с тремя дырками (см. рис. 9).

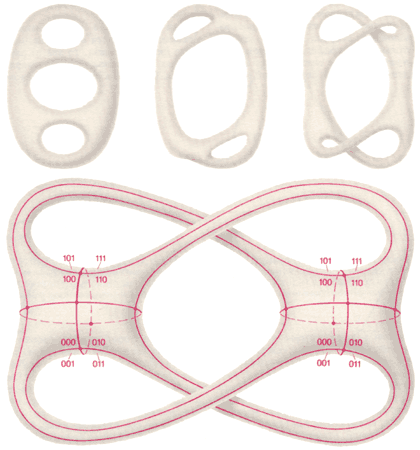Рис. 9. Восемь абстрактных шестиугольников при склеивании образуют конфигурационное пространство шарнирного механизма, состоящего из трёх двузвенных кривошипов. Каждый шестиугольник отвечает одному из восьми способов расположения трёх двузвенных кривошипов при фиксированном внутри плоского криволинейного шестиугольника положении центрального шарнира. Положение, в котором колено двузвенного кривошипа лежит справа от отрезка, соединяющего начало первого стержня с концом второго, помечено цифрой 0; противоположное положение колена помечено цифрой 1. Абстрактные шестиугольники оказываются помеченными трёхзначными двоичными числами. Чтобы более наглядно показать примыкание этих шестиугольников друг к другу в конфигурационном пространстве, можно расположить их на поверхности кренделя с тремя дырками, деформируя их так, как будто они сделаны из резины. Для большей симметрии картины поверхность кренделя с тремя дырками предварительно преобразуется в топологически эквивалентное ей многообразие, изображённое в нижней части рисунка. Трёхзначные двоичные числа, которыми помечены шестиугольники, указывают способ склеивания. Если двоичные метки двух шестиугольников совпадают в двух из трёх разрядов, то такие шестиугольники склеиваются вдоль двух противоположных сторон. Эти стороны определяются теми двумя сторонами плоского криволинейного шестиугольника, которым отвечает выпрямление двузвенного кривошипа с тем же номером, что и номер совпадающего двоичного разряда. Каждые четыре шестиугольника, метки которых совпадают в одном разряде, в конфигурационном пространстве имеют общую вершину. Диаметрально противоположные вершины этих четырёх шестиугольников соединяются в другой точке конфигурационного пространства. Эти две точки изображают конфигурации, в которых выпрямлены два двузвенных кривошипа с номерами, отвечающими номерам двух пар несовпадающих двоичных разрядов.

Наглядное изображение многообразия вроде кренделя с тремя дырками удобно благодаря своей конкретности, но у него есть и ряд недостатков. Например, изображая это многообразие в обычном пространстве, приходится отказаться от многих симметрий, присущих его абстрактному описанию. В первоначальном описании конфигурационного пространства системы трёх двузвенных кривошипов каждый шестиугольник конгруэнтен любому другому. Кроме того, поворот любого шестиугольника на угол 120° и 240° оставляет его неизменным. Однако при наглядном изображении конфигурационного пространства большая часть симметрии теряется. Шестиугольники на кренделе с тремя дырками не конгруэнтны и не имеют вращательной симметрии: повороты любого из них на 120° и 240° нельзя сделать без изменения его формы.

Другое «неудобство» кренделя с тремя дырками вызвано изменением геометрических свойств его поверхности от точки к точке: свойства поверхности на внешнем обводе отличаются от её свойств вблизи одной из дырок. Следует подчеркнуть, что геометрические свойства, о которых мы говорим, являются «внутренними» для этой поверхности. Внутренняя геометрия поверхности определяется результатами тех измерений, которые можно провести на ней самой, не обращаясь к окружающему её пространству. Эту геометрию следует отличать от внешней геометрии поверхности, которая описывает, каким образом поверхность вложена в пространство. Например, внутренняя геометрия цилиндра или конуса, полученного изгибанием плоского листа бумаги, та же, что и у этого плоского листа, хотя их внешние геометрии совершенно различны.

Поэтому тот факт, что со стороны поверхность выглядит неравномерно искривлённой, не является надёжным показателем того, что это свойство её внутренней геометрии. В чём заключается внутреннее отличие наружных участков поверхности кренделя от участков вблизи дырок? Вообразим, что из наружной выпуклой части кренделя вырезан маленький кусочек и распластан на столе. При этом он разорвётся подобно апельсиновой корке. Обратный процесс часто практикуется портным при изготовлении деталей одежды, которые должны принимать выпуклую форму (например, лиф платья). Из ткани удаляется клин, называемый вытачкой, и края выреза сшиваются друг с другом.

Однако, если маленький кусочек вырезан из поверхности кренделя вблизи дырки, то при попытке распрямить его на столе он сморщивается и накладывается сам на себя. Портной может обратить этот процесс, делая продольный разрез в ткани и вшивая в него дополнительный клин. Эта конструкция используется для изготовления юбки, узкой вверху и расклешённой внизу. Будет ли готовая деталь одежды на плоской поверхности разрываться, складываться или плотно примыкать к поверхности — это важная характеристика её внутренней геометрии.

Внутренняя геометрия поверхности бублика с одной дыркой меняется от точки к точке так же, как у кренделя с тремя дырками. При этом, как мы уже подчёркивали, бублик с одной дыркой и квадрат, противоположные стороны которого отождествлены, имеют одну и ту же топологию. Однако внутренняя геометрия квадрата значительно проще, чем у бублика с одной дыркой: в малой окрестности любой точки квадрата она совпадает с внутренней геометрией кусочка плоскости. Это свойство верно даже для точек на сторонах и в вершинах квадрата. Иначе говоря, для квадрата с отождествленными противоположными сторонами внутренняя геометрия любой малой области на нём одинакова. Внутренняя геометрия, обладающая такого типа равномерностью, называется локально-однородной.

Введение понятия локальной однородности имело большое значение для изучения двумерных многообразий. Около ста лет назад было доказано, что любую поверхность, а не только бублик с одной дыркой, можно реализовать таким образом, что её геометрия будет локально-однородной. Кроме того, на каждой поверхности может существовать лишь один тип локально-однородной геометрии.

Для поверхностей существует только три типа локально-однородных внутренних геометрий. Первый тип — это просто евклидова геометрия плоскости. Длина окружности на плоскости равна диаметру, умноженному на π, а сумма внутренних углов треугольника составляет 180°. Говорят, что плоскость имеет нулевую гауссову кривизну. Гауссова кривизна, впервые введённая Карлом Фридрихом Гауссом, представляет собой числовую характеристику внутренней формы поверхности.

Второй тип локально-однородной внутренней геометрии — это геометрия поверхности сферы. Отрезанная от сферы круглая «шапочка» при распла-стывании на плоскости разрывается точно так же, как выпуклый кусочек кренделя. Значит, длина окружности круга на сфере меньше длины окружности плоского круга, имеющего такой же радиус. Этот «дефект» длины границы круга на сфере объясняет происхождение стандартного названия локально-однородной геометрии сферы: эллиптическая геометрия (от греческого слова ελλειψιζ — недостаток, изъян). Сумма внутренних углов треугольника, построенного на сфере, превышает 180°; эта сумма тем больше, чем больше отношение площади треугольника к площади поверхности сферы (см. рис. 10). Сфера имеет постоянную положительную гауссову кривизну.

Как и следовало ожидать, кружок, вырезанный из поверхности с локально-однородной геометрией третьего типа, при распластывании на плоскости частично налегает сам на себя подобно близкому к дырке кусочку поверхности кренделя. Длина окружности такого кружка больше длины окружности соответствующего круга на плоскости. Поэтому эта геометрия называется гиперболической (от греческого слова νπερβολη — превосходство, избыток). Невозможно задать всю гиперболическую поверхность какой-нибудь одной аналитической формулой, но можно приближённо смоделировать большие её куски (см. рис. 11). Сумма внутренних углов треугольника на такой поверхности меньше 180°; чем больше площадь треугольника, тем меньше сумма его внутренних углов. Гиперболическая поверхность имеет постоянную отрицательную гауссову кривизну.

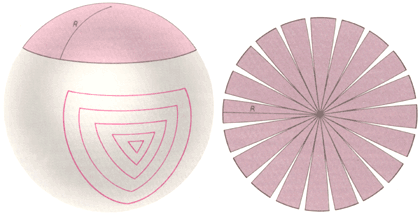Рис. 10. Геометрия сферы, называемая эллиптической, отличается от обычной евклидовой геометрии плоскости. Так, сумма внутренних углов сферического треугольника уже не равна 180° и увеличивается при увеличении его площади (слева). Отрезанная от сферы круглая «шапочка» при распластывании треснула бы и разорвалась, как показано справа. Площадь круга на сфере меньше площади плоского круга того же радиуса. Сфера имеет постоянную положительную кривизну.

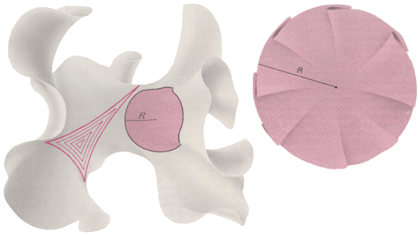Рис. 11. Геометрия поверхности постоянной отрицательной кривизны (слева) называется гиперболической. Сумма внутренних углов треугольника на такой поверхности меньше 180° и уменьшается при увеличении площади треугольника. Круг, вырезанный из гиперболической поверхности, при распластывании будет сморщиваться и накладываться сам на себя, как показано справа. Его площадь больше площади плоского круга того же радиуса. Бумажную модель гиперболической поверхности можно склеить из нескольких равносторонних треугольников так, чтобы в каждой вершине сходились семь треугольников.

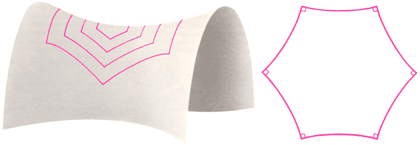Рис. 12. Углы правильного шестиугольника можно уменьшить, «растягивая» его на гиперболической поверхности. На рисунке шестиугольник растянут до положения, в котором все углы становятся прямыми. Восемь шестиугольников в конфигурационном пространстве системы трёх двузвенных кривошипов склеиваются по четыре в одной вершине, поэтому все их внутренние углы должны быть прямыми. Если каждый из этих шестиугольников деформировать в гиперболический шестиугольник с прямыми углами и, как и раньше, абстрактно склеить, то полученное двумерное многообразие будет иметь постоянную отрицательную кривизну. Говорят, что его геометрия локально-однородна. Этот приём значительно упрощает геометрию конфигурационного пространства.

Интересно показать, как можно задать локально-однородную геометрию на кренделе с тремя дырками. Вспомним, что шестиугольники, из которых первоначально было построено многообразие, можно изгибать и деформировать любым способом, лишь бы не было разрезов или разрывов. Метод состоит в следующем: каждый шестиугольник деформируют так, чтобы он имел локально-однородную геометрию, но по-прежнему примыкал к другим шестиугольным кускам многообразия, как на кренделе с тремя дырками.

Мы знаем, что на кренделе с тремя дырками в каждой вершине сходятся четыре из восьми шестиугольников. Если бы это были евклидовы шестиугольники, то сумма углов при каждой вершине равнялась бы 180°, что невозможно. Если бы геометрия шестиугольников была сферической, то сумма углов при вершине стала бы ещё больше, что тоже невозможно. Однако на гиперболической плоскости чем больше многоугольник, тем меньше его внутренние углы. Достаточно большой шестиугольник на гиперболической плоскости должен иметь внутренние углы 90°, и четыре таких шестиугольника плотно прилегают друг к другу в вершине. Следовательно, если восемь шестиугольников, расположенных на гиперболической плоскости, растягивать на ней до тех пор, пока их внутренние углы не достигнут 90°, то склеенное из них многообразие будет иметь локально-однородную гиперболическую геометрию. В этой новой форме многообразие уже труднее наглядно представить, но его геометрические свойства гораздо проще.

Читатель может доставить себе удовольствие и проверить, что поверхность любого кренделя с двумя или более дырками можно разрезать на шестиугольники, сходящиеся по четыре в каждой вершине. Если строить такое многообразие из гиперболических шестиугольников с подходящими внутренними углами, то на нём можно ввести гиперболическую геометрию. Более традиционный способ состоит в разрезании поверхности вдоль нескольких кривых («разрезов»), исходящих из одной точки, так что в итоге она полностью «раскрывается» и получается многоугольник, все вершины которого на поверхности склеены в одну точку. Например, поверхность кренделя с тремя дырками можно таким разрезанием превратить в двенадцатиугольник (или в восемь шестиугольников). Многоугольник, полученный разрезанием достаточно сложной поверхности, должен иметь по крайней мере шесть сторон. Если все внутренние углы такого многоугольника равны, то они должны быть меньше, чем у соответствующего правильного многоугольника на евклидовой плоскости. Это уменьшение углов достигается растяжением многоугольника на гиперболической плоскости. При попарном склеивании сторон многоугольника получается поверхность, топологически идентичная прежней, но имеющая локально-однородную геометрию, «унаследованную» от гиперболической плоскости.

Существуют только четыре замкнутые поверхности, локально-однородная геометрия которых не гиперболическая; полученные при разрезании этих поверхностей многоугольники имеют меньше шести сторон. Из бублика с одной дыркой получается квадрат, и все четыре угла квадрата могут быть склеены без изменения их величин. А раз нет необходимости в деформации, то возникающая локально-однородная геометрия на двумерном торе — евклидова. Аналогичным образом сфера и неориентируемое двумерное многообразие, называемое проективной плоскостью, снабжается эллиптической геометрией, а на неориентируемом многообразии, называемом бутылкой Клейна, задаётся евклидова геометрия.

Трёхмерное многообразие может искривляться примерно так же, как и поверхность: если трёхмерное многообразие имеет положительную кривизну, то любой его двумерный срез при распластывании на обычной евклидовой плоскости разорвётся; если же кривизна трёхмерного многообразия отрицательна, то при такой процедуре любой его двумерный срез сморщится и частично наложится сам на себя. Эллиптическая, гиперболическая и евклидова геометрии поверхностей имеют соответствующие трёхмерные аналоги.

В 1976 году один из нас (Тёрстон) пришёл к мысли, что при помощи локально-однородной гиперболической геометрии удастся понять структуру большинства трёхмерных многообразий. Это явилось сюрпризом для многих топологов, поскольку трёхмерные многообразия устроены гораздо сложнее, чем двумерные. В то время как ориентируемые двумерные многообразия можно перечислить, поскольку они полностью характеризуются своим родом, каждое трёхмерное многообразие, подобно перепутанной верёвочной петле, имеет, казалось бы, свои собственные, лишь ему присущие свойства и не подходит ни под какую схему классификации. Однако при более тщательном изучении такая схема всё же обнаруживается. Основой для этого служит то обстоятельство, что на многих трёхмерных многообразиях можно задать локально-однородную геометрию.

Как можно «навязать» многообразию такую простую геометрическую структуру? Во многих случаях применима процедура, аналогичная уже описанной нами для двумерных многообразий. Путём разрезания многообразие превращается в многогранник, и надо определить, сколько вершин многогранника должны совместиться при обратном абстрактном склеивании. Например, все 20 вершин додекаэдра, порождающего пространство Зейферта–Вебера, абстрактно склеиваются в одну точку. Телесный угол при вершине евклидова додекаэдра слишком велик для того, чтобы 20 таких углов могли сойтись в одной точке. Однако если этот додекаэдр помещён в трёхмерное гиперболическое пространство, то его можно увеличивать в объёме до тех пор, пока телесные углы при всех вершинах не станут достаточно малыми, чтобы их можно было сомкнуть в одной точке (см. рисунок на обложке журнала). Когда противоположные грани такого гиперболического додекаэдра попарно абстрактно склеиваются (после поворота одной из них на 1/10 полного оборота), то полученное многообразие оказывается пространством Зейферта–Вебера с локально-однородной гиперболической геометрией.

Додекаэдральное пространство Пуанкаре тоже получается склеиванием граней додекаэдра, но при этом 20 вершин додекаэдра разбиваются на пять групп по четыре вершины в каждой и затем склеивается каждая четвёрка. Величина телесного угла при вершине обычного додекаэдра несколько меньше, чем нужно для плотного примыкания друг к другу четырёх углов группы. Но достаточно большой додекаэдр в пространстве положительной кривизны имеет углы как раз нужного размера. Такой «увеличенный» додекаэдр даёт возможность ввести в додекаэдральном пространстве Пуанкаре локально-однородную эллиптическую геометрию (см. рис. 15). В этой связи стоит напомнить, как задаётся локально-однородная геометрия на трёхмерном торе. При построении этого многообразия восемь вершин куба абстрактно склеиваются. Так как восемь телесных углов куба можно без искажений плотно приложить друг к другу в одной точке, то локально-однородная геометрия трёхмерного тора — евклидова.

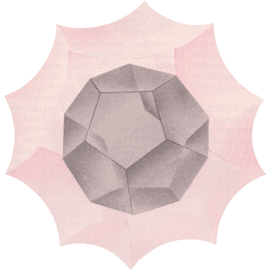Рис. 14. Многообразие Зейферта–Вебера можно наделить локально-гиперболической геометрией, если порождающему его додекаэдру позволить «расти» в гиперболическом пространстве. Рост многогранника в гиперболическом пространстве подобен растягиванию многоугольника на гиперболической поверхности. Когда додекаэдр увеличивается, телесные углы при его вершинах уменьшаются и каждая вершина становится всё острее. При абстрактном склеивании, дающем многообразие Зейферта–Вебера, все 20 вершин додекаэдра должны сойтись в одной точке. Поэтому телесные углы при вершинах нужно уменьшить в гиперболическом пространстве до таких размеров, чтобы 20 таких углов можно было плотно сомкнуть в одной точке.

Рис. 15. Додекаэдральное пространство Пуанкаре тоже получается из додекаэдра склеиванием пар противоположных граней, только при этом склеивании одна из двух граней поворачивается на 1/10 полного оборота, а не на 3/10, как при построении многообразия Зейферта–Вебера. Абстрактное склеивание приводит к тому, что в одной точке пространства сходятся четыре вершины додекаэдра. Телесный угол при вершине обычного додекаэдра несколько мал для того, чтобы четыре таких угла можно было плотно сомкнуть в одной точке. Но эти углы можно увеличить, «раздувая» додекаэдр в эллиптическом пространстве. Этот эффект противоположен тому, что происходит при раздувании многогранника в гиперболическом пространстве.

Чтобы не вводить читателя в заблуждение, надо отметить, что приведённые выше примеры в действительности не типичны, так как они слишком симметричны. Когда трёхмерное многообразие определяется с помощью склеивания граней неправильного многогранника, приходится больше заботиться о придании многограннику такой формы, которая приведёт к локально-однородной геометрии на полученном трёхмерном многообразии. Склеиваемые грани многогранника должны иметь одинаковую форму, а двугранные углы между гранями, примыкающими ко всем склеиваемым вместе ребрам, в сумме должны составлять 360°.

Между геометрией двумерных и трёхмерных многообразий имеются по крайней мере два главных различия. Во-первых, кроме упомянутых выше трёх типов геометрии на трёхмерных многообразиях существует ещё пять других типов локально-однородных геометрий. Эти дополнительные геометрии появляются потому, что при размерности многообразия, большей двух, внутренняя кривизна определяется для каждого двумерного сечения, проходящего через данную точку. Локально-однородные геометрии на разных двумерных сечениях не обязательно имеют одинаковую кривизну. Тем не менее представление о внутренней кривизне для всех восьми типов трёхмерных геометрий может быть составлено на основе геометрий двумерных многообразий.

Второе различие между двумерными и трёхмерными многообразиями, казалось бы, приводит к непреодолимым осложнениям. Трёхмерные многообразия можно скомбинировать таким образом, что получится новое трёхмерное многообразие, на котором нельзя задать локально-однородную геометрию. Однако топологи знают, как разбить трёхмерное многообразие на простейшие части чисто топологическими методами.

Один из нас (Тёрстон) высказал предположение, что это разбиение трёхмерного многообразия на простейшие части можно выполнить так, что каждая из частей допускает локально-однородную геометрию одного из восьми возможных типов. Это предположение было доказано для широкого класса многообразий, а также эмпирически проверено на многих других примерах (либо вручную, либо с помощью компьютера). Контрпримеров к высказанной гипотезе не обнаружено, и пока не похоже, что они вообще будут найдены.

Эмпирический анализ, кроме того, наводит на мысль, что для большинства трёхмерных многообразий усложнение их геометрии не играет роли. И действительно, было доказано, что на «большинстве» (в некотором точном смысле этого слова) трёхмерных многообразий можно задать локально-гиперболическую геометрию. Это открытие обнадёживает, так как гиперболические трёхмерные многообразия обладают многими красивыми свойствами. Например, Г. Мостов из Йельского университета в 1971 году доказал, что если на трёхмерном многообразии может быть задана локально-гиперболическая геометрия, то эта геометрия вполне определяется топологией многообразия. Из этой теоремы следует, что все многообразия, имеющие локально-однородную геометрию, в принципе можно расклассифицировать. Кроме того, для гиперболических трёхмерных многообразий теорема даёт грубый и простой критерий идентичности. Когда такое многообразие приведено к форме, в которой оно поддаётся геометрическому анализу, можно найти его объём, а теорема гарантирует, что этот объём зависит только от топологического типа многообразия. Часто при задании многообразий в общей топологической форме их очень трудно различить; объём служит удобным «индикатором» для каждого многообразия.

Учитывая эти результаты, можно вернуться к нашим первоначальным рассуждениям о топологической структуре Вселенной. Наблюдения свидетельствуют о том, что Вселенная всюду однородна и имеет эллиптическую, гиперболическую или евклидову геометрию. Есть также веские основания придерживаться теории, утверждающей, что в настоящее время Вселенная находится на стадии расширения, которая продолжается с момента так называемого Большого взрыва. Интересно, что ожидает Вселенную в отдалённом будущем? По-видимому, имеются лишь две возможности. Одна из них состоит в том, что гравитационные силы взаимного притяжения вещества Вселенной в конце концов остановят её расширение и приведут к новому коллапсу Вселенной в результате «большого сжатия». Другая возможность состоит в том, что гравитационное притяжение недостаточно сильно для того, чтобы остановить расширение Вселенной, и она будет расширяться вечно.

Согласно одному из следствий общей теории относительности, будущее Вселенной зависит от её геометрии. Если Вселенная имеет эллиптическую геометрию, то она в конце концов снова будет коллапсировать. Если её геометрия гиперболическая, то расширение будет продолжаться вечно. Если же геометрия Вселенной евклидова, то она тоже будет вечно расширяться, но скорость расширения будет стремиться к нулю. В принципе можно было бы узнать, какова геометрия Вселенной, наметив гигантский треугольник и точно измерив сумму его внутренних углов. Если бы сумма углов оказалась больше 180°, то геометрия пространства была бы эллиптической; если бы сумма углов была равна 180°, то геометрия была бы евклидовой; если же сумма оказалась бы меньше 180°, то геометрия была бы гиперболической. На самом деле космологи пытаются оценить среднюю плотность вещества во Вселенной и скорость её расширения, поскольку геометрию Вселенной можно связать с этими двумя характеристиками. Если при данной скорости расширения плотность вещества достаточно велика, то Вселенная снова будет коллапсировать.

Между тем широко распространено ошибочное мнение, что кривизна Вселенной определяет, конечна или бесконечна её протяженность. Часто считают, что если Вселенная конечна, то её геометрия должна быть эллиптической, и наоборот, если геометрия Вселенной гиперболическая, то Вселенная должна быть бесконечной. Пример пространства Зейферта–Вебера, являющегося трёхмерным многообразием с локально-гиперболической геометрией, показывает, что ни одно из этих убеждений не соответствует действительности. На самом деле большинство конечных топологических моделей Вселенной — это трёхмерные многообразия, подобные многообразию Зейферта–Вебера с локально-гиперболической геометрией. Такие многообразия дают модели конечной постоянно расширяющейся Вселенной.