
Интеграл
помогает доказать
неравенство Коши
 |
С. Берколайко Интеграл помогает доказать неравенство Коши |
[Решил добавить к уже выложенным доказательствам неравенства между средним арифметическим и средним геометрическим ещё одно. Оно не такое потрясное по оригинальности как доказательства Бора и Гурвица, а любопытно, скорее, простотой используемых средств и ловкостью автора.
Пусть a1, a2, ..., an – положительные числа, среди которых есть различные. Тогда выполняется неравенство Коши:
|
(1) |
Обозначим левую часть неравенства Коши через Sn и докажем его в такой форме:
| (Sn ) n > a1 a2 ... an . | (2) |
Очевидно, не ограничивая общности, можно считать, что для некоторого k такого, что
| a1 ≤ a2 ≤ ... ≤ ak ≤ Sn ≤ ak+1 ≤ ... ≤ an–1 ≤ an. | (3) |
Основой доказательства неравенства (2) будет неравенство
|
(4) | |||||||||||||||||
где
| b – a b |
= ln | b a |
= | b – a a |
. |
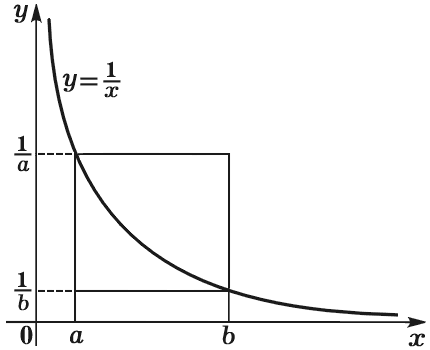
Из (3) и (4)
|
(5) |
или
|
(6) |
Опять-таки из (3) и (4)
|
(7) |
или
|
(8) |
Легко проверить, что левая часть неравенства (6) равна правой части неравенства (8). Значит, из (6) и (8)
|
(9) |
Поскольку среди чисел a1, a2, ..., an есть различные, в цепочке неравенств (3) какие-то неравенства выполняются «строго». Тогда эти «строгие» неравенства перейдут в (5) или (7). Значит, по крайней мере, одно из неравенств (6), (8) тоже будет «строгим». Поэтому вместо (9) мы можем утверждать
| ln | ak+1 ak+2 ... an (Sn) n–k |
< ln | (Sn)k a1 a2 ... ak |
, |
или
| ak+1 ak+2 ... an (Sn) n–k |
< | (Sn)k a1 a2 ... ak |
, |
откуда вытекает (2).
Если же
| a1 + a2 + ... + an n |
= | n | Ö | a1 a2 ... an |
. |