Е. Я. Гик О силе шахматных фигур

Если вы умеете играть в шахматы, то наверняка знаете, что лёгкую фигуру (коня или слона) можно смело отдать за три пешки, а ферзя за две ладьи; конь и пара пешек компенсируют потерю ладьи и т.д. Конечно, истинная сила фигуры зависит от конкретной позиции: вы без труда приведёте примеры, когда одна пешка матует вражеского короля, окружённого всей армией своих фигур. И всё же ясно, что каждая фигура в шахматной игре имеет некоторую среднюю силу. Для сравнения сил фигур за единицу обычно принимают силу пешки, выражая через неё силы остальных фигур. В учебниках, как правило, предлагается такая шкала:

(через F_x мы обозначаем силу фигуры x).

Эта шкала подтверждается многочисленной практикой и опытом шахматистов. Однако существуют и чисто математические пути определения силы шахматных фигур. Один из наиболее распространённых способов связан с подвижностью фигур. Рассмотрим для примера ходы короля (рис. 1). С каждого из угловых полей он может сделать 3 хода, с неугловых полей крайних вертикалей и горизонталей — по 5 ходов, наконец, с остальных полей доски король в состоянии переместиться на любое из 8 соседних полей. Суммируя, получаем число возможных ходов короля на шахматной доске, обозначим это число через S_Кр:

Из рисунков 2–6 находим числа S_x для других фигур:

Если мы теперь разделим S_x (число возможных ходов фигуры x) на N_x (число полей, на которых эта фигура может стоять), то получим среднее число ходов фигуры с одного поля доски. Назовём это число P_x подвижностью фигуры x:

Очевидно, N_x = 64 для всех фигур, кроме пешки, а N_п = 48. По формуле (*) находим:

Будем считать, что сила фигуры прямо пропорциональна её подвижности. Принимая, как и выше, силу пешки F_п за единицу, силы остальных фигур выразим через неё по формуле

В результате получится следующая шкала (значения округлены до десятых долей):

В вычислениях мы для простоты не учитывали возможность рокировки, а для пешки рассматривали также диагональные ходы, которые она совершает при взятии. На рисунках 1–6 выделены поля, с которых соответствующая фигура может сделать максимальное число ходов. Эти поля сосредоточены в центре, лишь ладья одинаково «сильна» на всех полях доски.

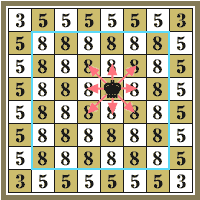Рис.1. Подвижность короля	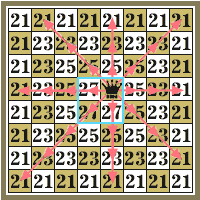Рис.2. Подвижность ферзя	Рис.3. Подвижность ладьи
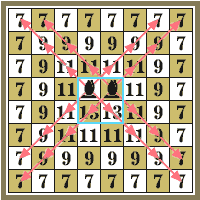Рис.4. Подвижность слона	Рис.5. Подвижность коня	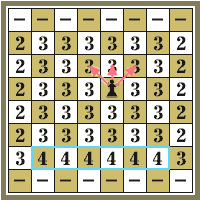Рис.6. Подвижность пешки

Король в полученной шкале получил очень низкую оценку, хотя на самом деле его «потеря» невозместима. (При программировании на ЭВМ для силы короля обычно выбирают очень большое число, подчеркивая этим его исключительность.) Однако с точки зрения подвижности найденная оценка вполне отвечает действительности. Наша шкала имеет и некоторые расхождения с практикой. Её основной дефект заключается в слишком большом превосходстве дальнобойных фигур (ферзя, ладьи и слона) над конём. В шахматах действия дальнобойных фигур почти всегда ограничены другими фигурами. Мы могли бы учесть это обстоятельство, вводя поправочные коэффициенты, но сейчас нас интересует сама идея, и на деталях мы не останавливаемся.

Математический подход к оценке силы фигур позволяет рассматривать разнообразные обобщения. Представьте себе, что вы играете в шахматы привычными фигурами, но на необычной доске, например, размером 50×50. Исходя из одной интуиции, вам будет довольно сложно определить сравнительную силу фигур на этой доске. Например, ясно, что слон здесь сильнее коня, но вот насколько, сразу сказать трудно. Пользуясь введённым выше понятием подвижности, мы можем найти вполне разумные значения для силы фигур и на такой доске. Аналогичным образом можно исследовать силу фигур на цилиндрической, сферической, пространственной и других шахматных «досках».

Другое обобщение состоит в изменении правил движения фигур. Шахматные композиторы, специализирующиеся в «фантастических шахматах», изобрели десятки так называемых «сказочных» фигур: канцлер, кентавр, ночной сверчок, всадник, жук, леопард, гиппопотам, лев, зебра, имитатор, жираф   и другие. Канцлер может ходить как ладья и конь, кентавр — как конь и слон, всадник — дальнобойная фигура, совершающая непрерывные прыжки по маршруту обычного коня в одном направлении (например, a1 – b3 – c5 – d7 или а1 – с2 – е3 – g4), лев ходит через поле в любом направлении и т.д. Наш способ позволяет без труда находить и силу сказочных фигур.

1. Найдите подвижность P_x(n) каждой шахматной фигуры x на доске размера n×n, пользуясь формулой (*).
2. Как меняется подвижность фигур при неограниченном увеличении размеров доски?
3. На обычной доске ладья по силе равна слону и коню (14 = 8,75 + 5,25). На какой ещё доске это возможно? На доске какого размера одинаковую силу имеют король и слон?
4. Сколькими способами на доске размером n×n можно поставить двух ферзей, чтобы они не угрожали друг другу?
5. Сколькими способами можно поставить на доске n×n трёх ферзей, чтобы они не угрожали друг другу?
6. Кто сильнее на бесконечной шахматной доске — ферзь или две ладьи?
7. Определите подвижность и силу кентавра, канцлера, всадника и льва.
8. Какую подвижность на бесконечной доске имеет конь типа (a, b), передвигающийся на a полей в одном направлении и на b полей — в перпендикулярном (обычный конь получается при a = 2, b = 1)?

Новые правила проведения матча на первенство мира по шахматам в принципе допускают ситуацию, при которой матч может продолжаться до бесконечности или до полного истощения одного или обоих участников.

А может ли сама шахматная партия длиться бесконечно долго?

Если на доске возникла матовая позиция, то ясно, что сколь долго бы ни длилась данная партия до наступления этой позиции, она окончится за конечное число ходов. Таким образом, результативная партия не может быть бесконечной. В ничейной же позиции партия могла бы продолжиться бесконечно, если бы в правилах шахмат не было специальных оговорок.

Напомним известное правило о ничьих в шахматной партии: если на доске три раза или более возникает одна и та же позиция, то в этот момент вы имеете право потребовать ничью. Говоря, что позиция одна и та же, мы имеем в виду, что одни и те же фигуры занимают одни и те же поля. При этом очередь хода должна быть за одной и той же стороной и внутренние возможности позиции тоже должны быть одинаковыми (это касается рокировки и взятия пешек «на проходе»).

Будем считать, что при троекратном повторении позиции ничья наступает автоматически. Тогда из конечности числа шахматных позиций следует, что продолжительность шахматной партии ограничена сверху. Обозначим число различных позиций на доске через A.

Упражнение 1. Найдите какую-нибудь верхнюю оценку для A.

Ясно, что тогда ни одна партия не может продолжаться более чем 3A ходов (под ходом мы понимаем два полухода — белых и чёрных). Действительно, за это время по крайней мере одна позиция повторится трижды (при очереди хода у одной и той же стороны), и, если партия не закончилась раньше, то в игру вмешается судья и зафиксирует ничью. Следовательно, при нашем предположении (которого нет в шахматном кодексе!), правило о троекратном повторении позиции исключает бесконечную партию.

Предположим теперь, что ничья наступает при троекратном повторении не одной и той же позиции, а одной и той же серии ходов подряд. Покажем, что при этом условии может существовать, бесконечная шахматная партия, т.е. существует такая партия, в которой никакая серия ходов не повторяется три раза подряд.

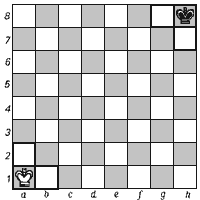Рассмотрим простейший случай, когда на доске перемещаются только короли. Более того, каждому из них разрешим маневрировать всего на трёх полях! Пусть белый король перемещается в левом нижнем углу — по полям a1, a2, b1, а чёрный в правом верхнем — по полям h8, h7, g8 и других фигур на доске нет. Обозначим ход каждого короля по часовой стрелке через 1, а против часовой стрелки через 2. Если начальное положение королей зафиксировано, то всякому их передвижению соответствует определенная последовательность из единиц и двоек. Верно и обратное: любая последовательность из единиц и двоек задаёт некоторое передвижение королей. Если, например, короли стоят на угловых полях (белый — на a1, черный — на h8), то последовательности 12 21 21 12 21 12 соответствуют такие ходы: 1. Kp a1 – a2 (первый член последовательности 1 — белый король идёт по часовой стрелке). 1 ... Кр h8 – g8 (второй член 2 — чёрный король идёт против часовой стрелки). 2. Кр a2 – a1 Кр g8 – h8. 3. Кр a1 – b1 Кр h8 – h7. 4. Кр b1 – a1 Кр h7 – h8. 5. Кр a1 – b1 Кр h8 – h7. 6. Кр b1 – a1 Kp h7 – h8.

Таким образом, на языке математики наша задача может быть сформулирована так: доказать, что существует такая бесконечная последовательность, состоящая из цифр 1 и 2, в которой нет трёх одинаковых рядом стоящих групп цифр. В книге А. М. и И. М. Ягломов «Неэлементарные задачи в элементарном изложении» (М., Гостехиздат, 1954. Задача 123б) доказано, что существуют сколь угодно длинные последовательности, состоящие из цифр 1 и 2, в которых нет одинаковых рядом стоящих трёх цифр.

В «Кванте» № 9 за 1975 год была напечатана статья Г. А. Гуревича «Бесповторные последовательности», в которой было доказано, что существуют бесконечные последовательности, состоящие из цифр 1 и 2, в которых нет одинаковых рядом стоящих трёх цифр. [Мелкий отрывок из этой статьи с основной идеей (да ещё конструктивной!) для построения такой последовательности. — E.G.A.]

Следовательно, существует, и бесконечная партия, в которой ни одна серия ходов не встречается три раза подряд.

Укажем теперь правила шахматного кодекса, которые исключают существование бесконечной партии.

Это, во-первых, «правило пятидесяти ходов»: если в течение 50 ходов подряд на доске не была взята ни одна фигура и ни одна пешка не сделала хода, то партия считается законченной вничью. Во-вторых, партия считается ничейной в том случае, если на доске возникла позиция, в которой выигрыш невозможен (король против короля, король против короля и лёгкой фигуры, король и слон против короля и слона «того же цвета»).

Пользуясь этими правилами, можно оценить число ходов самой длинной шахматной партии. Произведём соответствующие расчёты. Шестнадцать пешек в процессе игры могут сделать максимум 16×6 = 96 ходов. Пусть все эти ходы сделаны — тогда пешки взяли по крайней мере 8 фигур (если пешки, стоящие на одной вертикали, проходят «сквозь друг друга», то осуществляется хотя бы одно взятие). Если было произведено ровно 8 взятий, то ещё могут быть взяты 2×7 – 8 = 6 оставшихся фигур и 2×8 = 16 превращённых фигур, итого 6 + 16 = 22. Таким образом, общее число взятий и движений пешек не более 96 + 22 = 118.

Упражнение 2. Докажите, что если число движений пешек меньше 96, то общее число движений и взятий может только уменьшиться.

Поскольку между каждым продвижением пешки или взятием может быть сделано не более 50 ходов (точнее говоря, на 50-м ходу пешка должна продвинуться или фигура должна быть взята), а после последнего взятия партия сразу прекращается (на доске остались одни короли!), то общая продолжительность партии не более 50×118 = 5900 ходов.

Более тонкий (чисто шахматный!) анализ показывает, что самая длинная шахматная партия продолжается на два хода меньше — 5898.