Карандаш в петлице пиджака

Возьмите карандаш, сделайте в нем желобок около одного из концов, потом свяжите из веревки петлю так, чтобы длина веревки на петле была меньше удвоенного расстояния от желобка до другого конца карандаша (см. рис. 1). Теперь привяжите оставшимися концами веревки петлю к карандашу, охватывая карандаш по желобку, предварительно пропустив петлю в петлицу пиджака, а карандаш в петлю так, как показано на рис. 2. Желобок нужен для того, чтобы петля была жестко прикреплена к карандашу.

А теперь попытайтесь, не развязывая веревку, не разрывая ее, не ломая карандаша, снять карандаш с вашего пиджака.

Рис. 1

Рис. 2

С этой задачей связана небольшая история. В 1951 году замечательный советский математик, ныне член-корреспондент Академии наук СССР, И. Р. Шафаревич читал свой первый курс лекций в МГУ. Во время перерыва студенты показали ему эту задачу. Игорь Ростиславович попробовал один вариант, другой, но ... карандаш оставался на его пиджаке и на следующем часу лекции, и после нее.

Когда Игорь Ростиславович появился на следующей своей лекции через несколько дней, то карандаш продолжал украшать его пиджак. Однако лекция началась с того, что Шафаревич торжественно освободился от этого украшения.

А как получится у вас?

 Решение 

После нескольких неудачных попыток освободиться от карандаша вам очень захочется, чтобы карандаш мог сжиматься, хотя бы гнуться, или веревка смогла бы растягиваться. Стоп! А ведь, если бы веревка смогла бы растягиваться, то можно было бы освободиться от карандаша и другим способом. Взгляните-ка на рисунок. Представьте себе, если этот рисунок вам не совсем понятен, что вы оторвали от пиджака небольшой кусок вокруг петлицы. Как тогда освободить карандаш? «Ну и что из того, — скажете вы, — ведь веревка все равно не растягивается, а пиджак большой». А то, что пиджак не карандаш, он отлично гнется, и вместо того чтобы обводить петлю вокруг пиджака, можно отлично протащить пиджак сквозь петлю (достаточно лишь втащить в петлю кусок пиджака размером с длину карандаша, в чем легко убедиться экспериментально).

Кстати, Шафаревич, насколько я знаю, — единственный из отечественных математиков, чьё имя используется при обозначении математического объекта в РУССКОМ (!) написании. А именно, группа Тейта—Шафаревича обозначается буквой Ш (см., например, страницу 393 книги Анри Коэна). Есть примеры, когда имена российских математиков присутствуют не только в названии, но и в обозначении введённых ими понятий или объектов (например, полиномы Чебышёва T_n(x) от французского Tchebichef), но другого подобного случая использования русской буквы в западной математической литературе я не припомню. — E.G.A.

Амёба... в пиджаке

Эта история произошла в Москве летом 1966 года на Международном конгрессе математиков.

После одного из рабочих дней Конгресса в непринужденной обстановке собрались несколько математиков-топологов. Кроме советских ученых, среди них были выдающийся алгебраический тополог Дж. Ф. Адамс из Великобритании, его соотечественник, не менее известный геометрический тополог Е. К. Зиман и аспирант последнего Колин Рурк. Продолжался извечный спор о взаимоотношениях геометрии и алгебры. Темпераментный геометр Зиман нападал на алгебраиста Адамса, обвиняя его (а в его лице и всех алгебраистов) в отсутствии воображения и в практической беспомощности.

— Со всеми вашими изощренными алгебраическими инвариантами вы не в состоянии решить простейшие практические задачи, — сказал Зиман. — Вот, например, такую:

Зиман соединил большой и указательный пальцы на левой и на правой руках так, что получились два зацепленных кольца (рис. 1).

Рис. 1

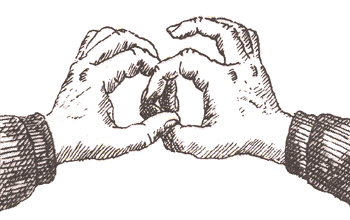
— Могу ли я расцепить эти кольца, не разжимая пальцы? — спросил он. — Я имею в виду, разумеется, что мое тело можно свободно деформировать (без разрывов и склеек), как тело амебы.

Адамс не спешил с ответом, и тут вступил в разговор доселе скромно молчавший аспирант Рурк.

— Нельзя, — уверенно заявил он.

— Как! — воскликнул Зиман. — Вы, мой ученик, геометр, не можете правильно решить такую простую задачу?! Я понимаю — эти беспомощные алгебраисты... Но вы!

Однако Рурк упорствовал. Вскоре, как водится среди англичан, было заключено пари. Тут же, на бумажной салфетке, Зиман нарисовал серию превращений амебы (рис. 2) и потребовал немедленной выплаты условленной суммы. Ответ Рурка был лаконичным:

— Да, но... вы — в пиджаке.

Рис. 2

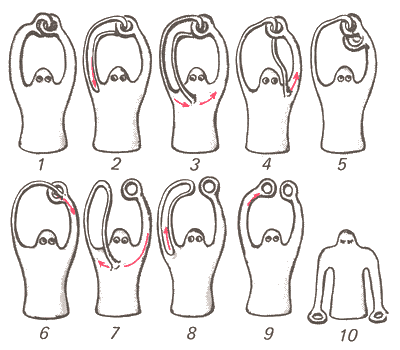
Зиман призадумался, а затем стал рассуждать вслух:

— Да, конечно, все эти деформации можно проделать и под пиджаком, но после этого пиджак уже не будет сидеть как прежде на амебе. Он будет связывать ей руки... Даже одного рукава для этого хватит.

Пока Зиман нехотя доставал из кармана бумажник, его окончательно расстроила завершающая эту историю реплика Адамса:

— Кстати, хотел бы я знать, как вы это докажете без инвариантов?

Добавлю ещё видеоверсию последнего ряда превращений (в качестве основы были использованы рисунки А. Т. Фоменко; см. ниже). Наряду с другими видеоматериалами, имеющими отношение к математике, она была показана на фестивале VideoMath во время работы Международного конгресса математиков в Берлине в 1998 году. Я тогда отвалил 40 кровных DM за кассету с этими "клипами", вот теперь выкладываю один. Может, под настроение и другие ролики из понравившихся оцифрую. Кстати, если кто был на Европейском конгрессе математиков в Барселоне в 2000 году, прикупил тамошний VideoMath DVD и не прочь поделиться, то свяжитесь со мной мылом. Очень уж любопытно, что там нового народ наваял с 1998 года. — E.G.A.

ТОПОЛОГИЧЕСКАЯ ЗАДАЧА «О РАСЦЕПЛЕНИИ ЗАЦЕПЛЕННЫХ ПАЛЬЦЕВ» Изображены этапы решения задачи наглядной топологии: как расцепить посредством гомеоморфизма человеческого тела пальцы рук, зацепленные как показано на первом рисунке? Разрешаются произвольные непрерывные деформации фигуры (гомеоморфизмы). Необходимая последовательность деформаций (изотопия) показана на последующих рисунках. Впрочем, здесь следует отметить одну тонкость. Успешное решение задачи, показанное нами, возможно лишь в том случае, когда человек «обнажен по пояс». Если, например, у него на руке надеты часы, то в конце описанной деформации пальцы рук, конечно, расцепятся, однако «завяжется» ремешок часов. A. Т. Фоменко. «Математика и миф сквозь призму геометрии». М., Изд-во МГУ, 2001.

На таких миниатюрных изображениях можно увидеть только общие черты. Если хочется разглядеть всё в деталях, то можно взять увеличенные (1260×1800) варианты тех же рисунков: 132 Кб, 82 Кб, 168 Кб, 144 Кб, 25 Кб. — E.G.A.