Г. Шестопал Как обнаружить фальшивую монету

Представьте себе, что на стол высыпана кучка совершенно одинаковых по виду монет, но вам сказали, что одна из этих монет — фальшивая. Она отличается от остальных монет по весу, но вам не сообщили, легче она или тяжелее. В вашем распоряжении имеются чашечные весы без гирь. Как нужно действовать, чтобы выделить эту монету и выяснить её тип (то есть узнать, легче она или тяжелее) за минимальное число взвешиваний?

Многие из вас, наверное, уже решали эту задачу для 12 монет. На рисунке приведено одно из решений этой задачи. Трём возможным исходам первого взвешивания соответствуют три различных варианта выбора монет для второго взвешивания: на рисунке левая стрелка соответствует случаю, когда перетянула левая чашка, средняя стрелка — равновесию, правая — случаю, когда перетянула правая чашка. Аналогичным образом изображены девять вариантов выбора монет для третьего взвешивания. (На рисунке монеты перенумерованы, буквы Л и Т означают соответственно, лёгкая и тяжёлая.)

Характерной особенностью этого решения является зависимость выбора монет для очередного взвешивания от результата предыдущего.

Поставим теперь задачу в общем виде.

Имеется m≥3 одинаковых по виду монет. Все монеты, кроме одной, имеют одинаковый вес, а одна отличается от них по весу, но неизвестно, в какую сторону. Каким наименьшим числом взвешиваний на чашечных весах без гирь можно найти эту монету и выяснить её тип? ¹

Эта задача более тридцати лет назад привлекла к себе внимание многих математиков, главным образом в Англии и США. В 1945 году в английском журнале «The Mathematical Gazette», похожем по своему направлению на «Квант», появилось решение этой задачи. Его автор Р. Л. Гудстейн впоследствии стал известным специалистом в области математической логики.

Гудстейн указал метод определения фальшивой монеты и её типа за n взвешиваний, n≥3, если число монет

(заметьте, что для трёх взвешиваний число монет не превышает двенадцати). Однако оказалось, что для n>3 его решение не является лучшим: за n взвешиваний можно выделить фальшивую монету и определить её тип из большего числа монет:

Это обнаружили независимо друг от друга сразу несколько математиков, и в следующем 1946 году тот же журнал опубликовал довольно длинный перечень их имён и разных ступеней успеха, достигнутых на поприще розыска фальшивой монеты. В этом же номере журнала напечатано самое лучшее решение — решение Ф. Дж. Дайсона, будущего известного физика-теоретика.

Идея Дайсона основана на использовании троичной системы счисления: все монеты маркируются специально выбранными троичными числами — маркерами, позволяющими удобно отражать ход последовательных взвешиваний. Особенно привлекательным при этом методе решения оказывается независимость выбора монет для последующего взвешивания от результата предыдущих.

В последующие годы были напечатаны другие решения этой задачи ², а метод Дайсона был незаслуженно забыт.

Поэтому интересно рассказать о нём подробно.

Всё решение Дайсона можно разбить на два этапа.

А	Если m = ½(3n – 3),       n = 2, 3, ..., то для выделения одной фальшивой монеты из общего числа m монет и определения её типа достаточно произвести n взвешиваний.
Б	Если m < ½(3n – 3),       m ≥ 3, то для достижения той же цели n взвешиваний также будет достаточно.

Рассмотрим каждый этап в отдельности.

Первый этап

Пусть число монет m = ½(3ⁿ – 3).

Рассмотрим все n-значные «троичные числа» (наборы из цифр 0, 1, 2) 00...00, 00...01, ..., 22...22. Их 3ⁿ. Используем их для маркировки монет следующим образом: в качестве маркеров возьмём все эти числа, за исключением трёх, состоящих из одинаковых цифр: 0...0, 1...1, 2...2.

«Построим» все маркеры в пары: в одну пару «поставим» два дополнительных маркера — таких, у которых цифры соответствующих разрядов в сумме составляют 2 (другими словами, дополнительными будут те маркеры, сумма которых равна 22...22).

Назовём маркер правым, если в нём первая слева пара неравных цифр — 01, 12 или 20. В противном случае маркер будем называть левым. Очевидно, в каждой паре дополнительных маркеров один всегда будет правым, другой — левым.

Заметим, что число пар маркеров как раз равно общему числу монет m. Перенумеруем монеты номерами от 1 до m и произвольно сопоставим каждой монете одну пару маркеров. Например, 12 монет можно «замаркировать» так, как показано в таблице.

Обозначим соответственно через M(i,0), M(i,1), и M(i,2), множество монет, для которых i-й разряд соответствующего им правого маркера равен 0, 1 или 2.

Легко видеть, что число монет в каждом из множеств M(i,0), M(i,1) и M(i,2) одинаково и что эти множества не имеют общих элементов (см., например, таблицу).

Метод взвешивания монет, придуманный Дайсоном, состоит в следующем:

Производится последовательно n взвешиваний монет.

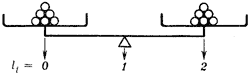При i-м взвешивании (i = 1, 2, ..., n) на левую чашку весов кладутся все монеты множества M(i,0), на правую чашку — все монеты множества M(i,2). Результат каждого взвешивания будем обозначать цифрой 0, если перевесила левая чашка весов, цифрой 1, если обе чашки имеют одинаковый вес, и цифрой 2, если перевесила правая чашка (см. рис.). Результат i-го взвешивания обозначим через l_i.

Из цифр l₁, l₂, ..., l_n составим маркер ³

Оказывается, l — маркер фальшивой монеты F и если l — правый маркер, то F тяжелее остальных монет, а если l — левый маркер, то F легче остальных монет.

Действительно, посмотрим, что происходит, когда производится i-e взвешивание. В результате этого взвешивания весы либо остались в равновесии, либо одна из чашек перевесила.

Если весы остались в равновесии, то фальшивой монеты на них нет, следовательно, она — в множестве M(i,1). Но это означает, что i-й разряд её правого (и левого) маркера равен 1, на что и указывает результат взвешивания l_i = 1.

Если одна из чашек весов перевесила, то фальшивая монета лежит на весах. Пусть, например, перевесила правая чашка, т.е. l_i = 2. Этот результат возможен в двух случаях:

— фальшивая монета лежит на правой чашке (тогда она тяжелее остальных монет), значит, она находится во множестве M(i,2), i-й разряд её правого маркера равен 2, следовательно, результат взвешивания совпадает с i-м разрядом её правого маркера;

— фальшивая монета лежит на левой чашке (тогда она легче остальных монет), значит, она находится во множестве M(i,0), следовательно, i-й разряд её правого маркера равен 0 и результат взвешивания совпадает с i-м разрядом её левого маркера.

Совершенно аналогичен «симметричный» случай, когда перевесит левая чашка весов (l_i = 0).

Поэтому, действительно, сформированный в результате последовательных взвешиваний маркер l = l₁ l₂ ... l_n есть маркер фальшивой монеты, притом правый в случае более тяжёлой монеты и левый — в случае более лёгкой, что и требовалось доказать.

Интересно отметить, что тип монеты, как правило, определится раньше, чем произведены все взвешивания, — как только в процессе формирования маркера l появятся две различные цифры.

Существенной особенностью описанного метода, как уже было отмечено раньше, является то обстоятельство, что выбор монет для каждого взвешивания не зависит от результатов предыдущих взвешиваний.

Например, для 12 монет, замаркированных так, как показано в таблице, нужно проделать такие три взвешивания: (1,4,7,10) – (3,6,9,12), (3,6,9,10) – (2,5,8,12), (3,4,8,12) – (2,6,7,11).

Второй этап

Коротко наметим метод Дайсона для случая m < ½(3ⁿ – 3).

Если в этом случае монетам сопоставлять маркеры произвольно, то в множествах M(i,0) и M(i,2) может оказаться разное число монет. Поступим поэтому следующим образом. Разобьём все маркеры на группы по шесть: в одну группу отнесём правые маркеры, получающиеся друг из друга циклической заменой цифр 0 → 1, 1 → 2, 2 → 0 и соответствующие им левые маркеры.

В каждой группе окажется по три правых маркера и три левых маркера. Группу, содержащую правые маркеры 00...01, 11...12, 22...20, выделим особо. Разобьём монеты на группы по три, пока это возможно, и замаркируем их следующим образом. Монетам из одной группы сопоставим пары маркеров из одной группы, а для остатка, если он есть, используем пары маркеров из выделенной группы. Если останется одна монета, не вошедшая в тройки, то сопоставим ей правый маркер 11...12, а если две, — то правые маркеры 00...01 и 22...20 (и соответствующие левые маркеры).

При такой маркировке первые n–1 взвешиваний производятся по старым правилам. Как производить последнее взвешивание, сообразите самостоятельно.

Метод Дайсона описан. Убедимся теперь, что он в определённом смысле является наилучшим. А именно, покажем, что если из m монет можно выделить n взвешиваниями фальшивую монету и определить её тип, то 2m ≤ 3ⁿ – 3. Разумеется, мы не будем учитывать возможного «везения»: при нём для определения фальшивой монеты из любого числа монет может хватить и двух взвешиваний.

Итак, предположим, что n взвешиваний достаточно.

Занумеруем монеты числами 1, 2, ..., m и приготовим 2m бумажек. Напишем на них все возможные варианты: первая монета легче, первая монета тяжелее, вторая монета легче и т.д. Ясно, что при этом все 2m бумажек окажутся использованными и ни один из возможных вариантов не будет упущен. Будем обозначать, как мы условились выше, результат взвешивания цифрами 0, 1 или 2. Каждое взвешивание показывает, что часть возможных ответов не подходит, а часть — остаётся под подозрением. Отберём монеты для первого взвешивания. Не производя его фактически, напишем на каждой из бумажек тот результат первого взвешивания, который оставляет её под подозрением. Ясно, что на каждой бумажке будет написана одна из цифр 0, 1 или 2. Таким образом, все бумажки будут разбиты на три группы. Поэтому в наиболее многочисленной группе окажется не меньше 2m/3 бумажек. Значит, как бы мы ни организовывали первое взвешивание, может оказаться, что после него под подозрением останутся не меньше 2m/3 бумажек.

Аналогично, второе взвешивание рассортирует эту подозрительную группу на три подгруппы. Поэтому в наиболее многочисленной из них окажется не меньше 2m/9 бумажек. Точно так же после n взвешиваний мы можем получить 2m/3ⁿ подозрительных бумажек в одной группе. Следовательно, если 2m/3ⁿ > 1, то фальшивая монета и её тип, вообще говоря, за n взвешиваний определены быть не могут. Поэтому если n взвешиваний достаточно, то 2m ≤ 3ⁿ.

Но это ещё не всё! Мы не разобрались ещё со случаем 2m = 3ⁿ – 1 (чётное число 2m не может равняться ни 3ⁿ – 2, ни 3ⁿ). Для него изложенных выше соображений недостаточно.

Рассмотрим более внимательно первое взвешивание. Ясно, что число бумажек, на которых написана цифра 0, равно числу бумажек, на которых написана цифра 2. Пусть тех и других — по p штук, тогда на 2m – 2p бумажках будет написана 1.

Заметим, что p — чётное число. Действительно, если на левой и правой чашке весов лежит по k монет, то p = 2k. Если p или 2m – 2p больше 3^n–1, то по рассмотренному для определения нужной бумажки может не хватить оставшихся n–1 взвешиваний. Если же p = 2k ≤ 3^n–1 и 2m – 2p ≤ 3^n–1 – 1, то, поскольку 3^n–1 — число нечётное, p ≤ 3^n–1 – 1, 2m – 2p ≤ 3^n–1 – 1. Но тогда 2m = (2m – 2p) + 2p ≤ 3^n–1 – 1 + 2(3^n–1 – 1) = 3ⁿ – 3. Итак, если n взвешиваний достаточно, то 2m ≤ 3ⁿ – 3.

В заключение — несколько задач, которые могут быть решены методом Дайсона.

1. Имеются две группы из m₁ и m₂ монет, причём известно, что одна монета — фальшивая, она легче, если принадлежит первой группе, и тяжелее, если принадлежит второй группе. За какое минимальное число взвешиваний можно выделить фальшивую монету?
2. Пусть, кроме групп m₁ и m₂, имеется группа m₃ из эталонных (заведомо не фальшивых) монет. Сколько взвешиваний необходимо в этом случае?
3. Имеется m монет, среди которых заведомо есть фальшивая (неизвестно, более лёгкая или более тяжёлая), и ещё одна эталонная монета. Можно ли определить фальшивую монету и её тип за n взвешиваний, если m = ½(3ⁿ – 3)? Сколько взвешиваний необходимо для других m?
4. Дано m монет и известно, что фальшивых монет среди них — не больше одной. За какое число взвешиваний можно найти фальшивую монету и определить её тип или убедиться, что фальшивой монеты нет?
5. В случае 2m < 3ⁿ – 3 последнее взвешивание зависело, вообще говоря, от результатов предыдущих взвешиваний. Постарайтесь добиться того, чтобы оно зависело от результатов возможно меньшего числа взвешиваний.