

|
 |
 |
Я ехал по Ленинграду в трамвае со своим племянником Мишей. Опустив в кассу 6 копеек, я оторвал два билета.
— Чур этот билет мой! — сказал Миша.
— Пожалуйста, бери любой из них. Они ведь совершенно одинаковые, с любым из них можно проехать весь маршрут.
— Одинаковые, да не совсем. Этот билет самый обыкновенный, на нем номер 286 357. А следующий билет с номером 286 358 — «счастливый», сумма первых трёх цифр совпадает с суммой последних трёх.
Тут я вспомнил, что уже не раз слышал о распространённом поверье: билет с одинаковыми суммами цифр приносит счастье. В данном случае Мише достался билет 286 358, в котором
— И часто тебе попадаются «счастливые» билеты? — спросил я.
— Да нет, очень редко. Примерно раз в месяц. А так как я езжу в институт и обратно каждый день, кроме выходных, то, значит, в среднем один «счастливый» билет приходится на 50 обычных.
— Чепуха, — вмешался один из наших попутчиков; — Я вошёл на предыдущей остановке и в той же кассе вытянул тоже «счастливый» билет — 286 349. Да и сейчас
— Это не вполне верно, — возразил новый пассажир, оторвавший «счастливый» билет 286 367. — Ваш пример ничего не доказывает. В следующем десятке будет ещё один «счастливый» билет — 286 394. А затем «счастливых» билетов долго не будет, вплоть до номера 286 439, так что здесь между двумя «счастливыми» билетами будет интервал в 45 билетов. Таких примеров можно привести много. В этой же катушке билетов, начальные цифры которых 286, между билетами 286 097 и 286 169, то есть среди 71 билета, нет ни одного «счастливого».
— Вот я и говорю, — подхватил Миша, — в среднем один «счастливый» билет попадается на полсотни.
— Это тоже опрометчивое заявление, — заметил я. — Чтобы правильно отнетить на этот вопрос, нужно его исследовать. А сначала нужно точно его сформулировать. Скажем, так: сколько существует «счастливых» шестизначных чисел от 000 000 до 999 999, то есть чисел, у которых равны суммы цифр первых трёх и последних трёх разрядов?
 — Ну что же, — сказал Миша после недолгого размышления, — я сейчас не могу точно ответить на этот вопрос, но могу описать способ, позволяющий его решить, по крайней мере, в принципе. Выпишем подряд все числа от 000 000 до 999 999 и проверим каждое из них. Таким образом мы сможем пересчитать число «счастливых» билетов.
— Ну что же, — сказал Миша после недолгого размышления, — я сейчас не могу точно ответить на этот вопрос, но могу описать способ, позволяющий его решить, по крайней мере, в принципе. Выпишем подряд все числа от 000 000 до 999 999 и проверим каждое из них. Таким образом мы сможем пересчитать число «счастливых» билетов.
— Да, такой метод решения возможен. Он называется методом перебора. Им можно решать задачи, в которых исследуются свойства конечного набора каких-либо чисел или других объектов. Однако метод перебора имеет два недостатка. Прежде всего, он очень трудоёмок. Рассуди сам, необходимо проверить миллион чисел. Если на проверку каждого из них тратить всего 1 секунду, то потребуется 1 000 000 секунд, то есть почти 278 часов. При восьмичасовой ежедневной работе это займет 35 дней.
— Но ведь можно поручить это электронной вычислительной машине!
— Можно, конечно, но стоит ли «палить из пушки по воробьям»? Кроме того, метод перебора имеет и другой недостаток, который сохраняется и при расчете на ЭВМ. При переборе получается решение только одной конкретной задачи, которое обычно не позволяет произвести обобщения или вскрыть какие-либо неизвестные закономерности.
— Разрешите мне опять вмешаться в ваш разговор, — сказал обладатель счастливого билета 286 367. — Я заинтересовался вашей задачей и уже нашел её решение, правда, не точное, а приближённое, вернее то, что мы, математики, называем оценкой. Да, я не представился, зовут меня Георгий Владимирович, я доцент кафедры математики одного из технических вузов. Так вот, молодой человек, — обратился он к Мише, — давайте введём новое определение «счастливого» билета, или, лучше даже, введём новый термин, например, «красивый» билет. Будем называть билет «красивым», если сумма первых трёх цифр даёт тот же остаток при делении на 9, что и сумма следующих трёх цифр. Понятно?
— Понятно, — ответил /Миша, — но почему именно на 9?
— А потому, что в нашей десятичной системе счисления всякое число даёт тот же остаток при делении на 9, что и сумма его цифр. Это свойство даёт возможность легко найти число «красивых» билетов. Действительно, среди чисел от 1 до 999 ровно 111 дают при делении на 9 остаток 1, столько же остаток 2, и так далее.
Сколько же существует различных «красивых» чисел с остатком 1? На первом месте может стоять 111 чисел и для каждого из них следом можно поставить любое из тех же 111 чисел. Таким образом, получаем
— А при чём же здесь «счастливые» билеты? — спросил Миша.
— Это уже совсем просто! Ведь если равны суммы цифр, то равны и их остатки при делении на 9, следовательно, каждый «счастливый» билет является «красивым». Однако не всякий «красивый» билет будет «счастливым». Например, билет 100 748 будет «красивым», но не будет «счастливым». Итак, если обозначить число «счастливых» билетов через C, то можно написать неравенство
— Но это всё-таки не полное решение задачи, — сказал Миша. — Мы получаем, что «счастливых» билетов меньше 111 112, но не знаем, насколько. А можно ли показать, что их больше
— Можно дать и оценку снизу,— ответил Георгий Владимирович,—боюсь только, что она будет довольно грубой. Назовём «прекрасными» билетами такие, у которых номер состоит из двух совершенно одинаковых половинок, например 287 287. Таких билетов ровно 1000, а именно, 000 000, далее 001 001,
Здесь оценка сверху более чем в 100 раз превышает оценку снизу, так что вряд ли такой результат можно считать решением поставленной задачи.
— Пожалуй, оценку сверху можно несколько улучшить, — сказал я, — используя признак делимости на 11.
— Что это за признак? — спросил Миша. — Мы его не проходили.
— Он очень прост. Сложим все цифры, стоящие в нечётных разрядах, потом отдельно сложим числа, стоящие в чётных разрядах. Так вот, если разность полученных сумм делится на 11, то и всё число делится на 11, и наоборот, любое число, делящееся на 11, обладает этим свойством.
— Какое же отношение этот признак имеет к «счастливым» билетам?— удивлённо спросил Миша.
— Самое прямое, но скажи сначала, слышал ли ты о билетах, «счастливых по-московски»?
— Ах, да! Москвичи считают билет «счастливым», если сумма цифр, стоящих на чётных местах, равна сумме цифр, стоящих на нечётных местах. Вот чудаки!
 — Во-первых, чудаком являешься ты, если веришь, что «счастливые» билеты могут приносить удачу, а во-вторых, москвичи называют «счастливыми» те же самые билеты, что и ленинградцы, а билеты, которые мы называем «счастливыми по-московски», они называют «счастливыми по-ленинградски». Так «американские горки» в Америке называют «русскими». Но не в этом дело. Совсем легко проверить, что номера билетов, которые ты называешь «счастливыми по-московски», делятся на 11. Верно?
— Во-первых, чудаком являешься ты, если веришь, что «счастливые» билеты могут приносить удачу, а во-вторых, москвичи называют «счастливыми» те же самые билеты, что и ленинградцы, а билеты, которые мы называем «счастливыми по-московски», они называют «счастливыми по-ленинградски». Так «американские горки» в Америке называют «русскими». Но не в этом дело. Совсем легко проверить, что номера билетов, которые ты называешь «счастливыми по-московски», делятся на 11. Верно?
— Верно, — ответил Миша.
— И этих билетов не больше, чем чисел от 0 до 999 999, делящихся на 11.
— То есть не больше 90 910! — воскликнул Георгий Владимирович.
— А каких билетов больше, — спросил Миша, — «счастливых» или «счастливых по-московски»?
— Совсем нетрудно установить, что одних столько же, сколько и других, — ответил я.
— Скажете тоже, «нетрудно», — хмыкнул Миша, — мы же не знаем, столько тех и других.
— А это и не нужно, — заметил Георгий Владимирович. — Расставь первые три цифры «счастливого» билета на чётные места, последние три цифры на нечётные места, и ты получишь из «счастливого» билета билет, «счастливый по-московски». И обратно, если у билета, «счастливого по-московски», собрать все цифры, стоящие на чётных местах, в первой половине номера, а остальные — во второй, то ты получишь «счастливый» билет. Таким образом, мы установили взаимно однозначное соответствие между теми и другими билетами. А отсюда следует, что их одинаковое количество. Верно?
|
— Верно! —воскликнул Миша.— Вот здорово! Значит, мы доказали, что «счастливых» билетов меньше, чем 90 910.
— А какова будет сумма цифр у номера, если в «счастливом» билете заменить три последние цифры на разности между 9 и этими цифрами?— спросил Георгий Владимирович.
— Сейчас, — задумался Миша, —
— Правильно, — ответил он.
— Но сколько же все-таки «счастливых» билетов? — взглянув на меня, спросил Миша.
— Ответ я тебе скажу сейчас: 55 252, то есть в среднем каждый
 |
Л. М. Финк Ещё раз о счастливых билетах |
Вчера мой племянник Миша вбежал ко мне с возгласом: «Дядя, я, кажется, решил!»
— Что ты решил?
— Задачу о счастливом билете. Помнишь,
— Как же, помню. Об этом нашем разговоре даже напечатали в «Кванте» (см. № 7 за 1975 г.,
— Почти.
— Что значит «почти»? Почти точное число?
— Нет, число-то точное. Но я всё-таки пользуюсь методом перебора. Правда, просматриваю не миллион шестизначных чисел, а в тысячу раз меньше.
— Расскажи-ка, как ты это делаешь.
— Я вычислил, сколько счастливых билетов имеют заданную сумму первых и последних трёх цифр, равную определённому числу, например k. Обозначим количество трёхзначных номеров с суммой цифр, равной k, через
| 001001 010001 100001 |
001010 010010 100010 |
001100 010100 100100 |
В общем же случае счастливых билетов с суммой цифр, равной k в каждой «половинке», будет
Миша радовался так, будто оторвал сразу несколько счастливых билетов.
— Поздравляю тебя с решением, — сказал я. — Вот только мне не ясно, каким образом ты определял значения
— Очень просто. Выписал тысячу трёхзначных чисел от 000 до 999 и подсчитал сумму цифр у каждого. Я справился с этим без всяких вычислительных машин — всего за одно воскресенье, — гордо ответил Миша.
— Что же, похвально. Но, пожалуй, полезнее было бы поискать формулу или правило, позволяющее находить
— Я пробовал, дядя, честное слово! Но ничего не получилось.
— Давай попытаемся вместе. Для начала слегка изменим обозначение: вместо
— А что означает эта тройка внизу?
— То, что мы рассматриваем трёхзначные номера.
— Но это и так ясно!
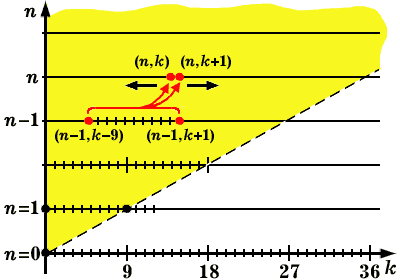
— Дело не в этом. Мы обобщим задачу и будем искать — Дядя, я не могу решить задачу для трёхзначных номеров, а ты хочешь решать её и для четырёхзначных, и для — Конечно, труднее, если пользоваться перебором. Но легче, если рассуждать логически. Между прочим, в истории математики известно немало задач, решить которые удалось лишь после того, как они были сформулированы в общем виде. Попробуй для начала найти — Сейчас подумаю. Нужно определить, сколько однозначных чисел имеет сумму цифр k. Но для однозначного числа сумма цифр совпадает с самим числом. Тут и решать нечего. Есть одно однозначное число с суммой цифр, равной нулю, — это 0; одно однозначное число с суммой цифр, равной единице, — это 1, одно число с суммой цифр, равной двум, — Отлично! Пойдём дальше. Предположим теперь, что мы уже знаем значения — Ясно, — ответил Миша. Значения причём, если По формуле (*) можно вычислить значения — Совершенно верно, — сказал я. — Формулы, аналогичные Миша взял листок бумаги и начал рисовать таблицу. Прежде всего он заполнил столбец для Затем по той же формуле были построены столбцы для — Теперь, — сказал Миша закончив таблицу, — можно подсчитать число счастливых билетов с двузначными, четырёхзначными, шестизначными и восьмизначными номерами. Для этого все числа в Проделав это, Миша получил: — Таким образом, — подытожил Миша, — на планете системы — Вот теперь, — сказал я, — можно считать поставленную задачу решённой.
— А нет ли других способов её решения? — спросил Миша.
— Вероятно, есть. Может быть, их придумают читатели «Кванта» и поделятся с нами? Не обязательно стараться найти точное число счастливых билетов, можно ограничиться оценкой или приближённой формулой, если эти оценки обеспечивают небольшую относительную погрешность. Вот, например, одна простая формула, выражающая количество √33nπ С увеличением n относительная погрешность быстро уменьшается.
— Как ты получил эту формулу, дядя?
— Сейчас это объяснить трудно. Я воспользовался методами теории вероятностей; надеюсь, что через несколько лет ты с этой теорией познакомишься. В этой книге задаче о счастливых билетах посвящено всего два абзаца, а математические приготовления к её решению изложены, как мне кажется, не лучшим образом — слишком много места уделено биномиальным коэффициентам и слишком мало производящим функциям. Так что я добавил сюда изложение похожей задачи из «Конкретной математики» Р. Грэхема, Д. Кнута и О. Паташника, в которой роль производящих функций показана гораздо чётче. Производящие функции
Выражение k!·(n – k)! — эти числа являются коэффициентами при xk в разложении Найдём, например, производящую функцию для числа способов представить N в виде суммы n слагаемых, каждое из которых равно одному из чисел В частности, если допустимыми значениями слагаемых являются числа Производящую функцию для чисел (1 – x)n Разлагая получаем где суммирование ведётся по всем k от 0 до Производящие функции можно написать для всех задач, решённых выше методом рекуррентных соотношений. Например, для задачи об уплате суммы в Счастливые троллейбусные билеты
Некоторые люди считают шестизначные номера троллейбусных билетов «счастливыми», если сумма первых 3 цифр равна сумме последних 3 цифр. Например, билет 615 372 «счастливый», так как Чтобы найти число счастливых билетов, заменим последние 3 цифры их дополнениями до 9. Например, вместо 615 372 возьмём 615 627. Тогда получится билет, сумма цифр которого равна 27 (например, Ещё одно отвлечение внимания от рассказа о счастливых билетах: фраза про «цифры и их дополнения до 9» напомнила один мелкий математический фокус. Этот вопрос уже обсуждался на страницах нашего журнала; было выяснено, что из миллиона билетов с шестизначными номерами (от 000 000 до 999 999) счастливых — 55 252, т.е. приблизительно один из каждых 18 билетов является счастливым.
Как водится у математиков, решалась и более общая задача — о количестве Но вот в редакцию пришли два письма. Первое прислали в феврале М. Мнацаканян и А. Меликян, а второе — в марте — Р. Айдагулов. И в том, и в другом содержится одна и та же явная формула для π sin x Интересно, что эта формула была получена совсем разными методами: М. Мнацаканян и А. Меликян пользуются производящими функциями (т.е. функциональным анализом), в то время как Р. Айдагулов опирается на метод тригонометрических сумм (аналитическая теория чисел). К сожалению, их доказательства, хотя и не сложные, всё же выходят за рамки школьной математики и не могут быть опубликованы в нашем журнале. Сейчас мы дадим элементарное доказательство Для этого обозначим через Так как n-значное число с суммой цифр k получается из Это и есть соотношение, о котором говорилось выше. Подставив в него Как пользоваться этим соотношением для вычисления Если при фиксированном n известны все и
Таким образом, формулы (2), (2'), (2") позволяют вычислить все числа Возьмём теперь любое счастливое Формула (3) даёт возможность вычислить число Чтобы доказать (1), положим
π sin x Оказывается, Из формул (3), (5) и (4) сразу следует (1). Таким образом, нам остаётся доказать (5), для чего достаточно проверить, что числа π sin x π sin x равносильное соотношению
π sin x sin x которое верно (легко сосчитать, что тригонометрическое выражение в квадратной скобке тождественно равно нулю).
Вспомним, что вместо (2') достаточно проверить любое другое соотношение на Внимательный читатель, наверное, задал себе вопрос — откуда взялась формула (4)? Конечно, формально можно считать, что мы её угадали так же, как мы «угадали» формулу (1). На самом же деле формула (4), как и формула (1), была извлечена из письма М. Мнацаканяна и А. Меликяна, т.е. использовался готовый результат. Ведь наш метод доказательства, в отличие от метода Р. Айдагулова и метода М. Мнацаканяна и А. Меликяна, не даёт возможности обнаружить формулу (1), а только позволяет проверить её.
В заключение предлагаем читателям доказать следующее обобщение формулы (1) для числа счастливых π sin x «Квант» уже не раз писал о счастливых билетах π sin x В этой замечательной формуле π sin x Г. А. Гальперин из Москвы и А. В. Корлюков из Гродно задались вопросом: что будет, если вычислять число счастливых билетов C2n, m по приближённой формуле
N N sin x Они обнаружили, что при любом Доказательство можно получить, слегка модифицировав вывод sin x можно представить как «тригонометрический многочлен»
для всякого такого многочлена выполнено равенство
π N N при достаточно Вычислять число счастливых билетов на компьютере удобнее по Пусть, например, длина билета равна 2, а система счисления десятичная. Тогда в sin2 (π/10) sin2 (3π/10) При других n и m читатели могут получить аналогичные равенства самостоятельно.
А. А. Михайлов из г. Стучка Латвийской ССР предлагает новый подход к задаче о счастливых билетах (1 – x)2n Чтобы найти этот многочлен, можно воспользоваться биномом Ньютона
где биномиальные коэффициенты
k! · (m – k)! Биномиальная формула верна и для отрицательных показателей m; при этом Если выразить оба сомножителя, входящих где квадратные скобки обозначают целую часть числа. Частный случай этой формулы для десятичной системы обнаружили также студенты из Иркутска Д. Балябин и С. Кривошеин.
Для числа обычных счастливых билетов получаем Как видите, формула (3) позволяет вычислить число счастливых билетов довольно просто!
Для C2n, 2 есть ещё более простое выражение. Действительно, в этом случае Кроме того, А. А. Михайлов отмечает, что число счастливых билетов совпадает с числом целых точек, лежащих строго внутри Статья составлена по материалам готовящейся к изданию книги «Лекции о производящих функциях», изд-во «Фазис» (лекции были прочитаны в Независимом Московском Университете). Советуем обратиться к этой книге за дополнительными примерами использования производящих функций для решения комбинаторных задач. Рассмотрим одну популярную в начале Билет назывался счастливым, если сумма первых трёх цифр его номера равнялась сумме последних трёх цифр.
Так, билеты с номерами 000 000 и 123 060 — счастливые, а билет с номером 123 456 — несчастливый. Считалось, что счастливый билет приносит счастье (особенно, если его съесть).
Возникает вопрос, сколько всего существует счастливых билетов? Или: какова вероятность покупки счастливого билета?
Человеку, владеющему элементарными навыками программирования, нетрудно написать программу для подсчёта числа счастливых билетов. Простейшая такая программа перебирает все номера от 000 000 до 999 999, отбирая среди них счастливые. Давайте, однако, попробуем обойтись без машины.
Разобьём все счастливые билеты на классы, в каждом из которых сумма первых трёх цифр одинакова. Эта сумма может принимать значения от 0 (для тройки цифр 000) до 27 (для тройки 999). Поэтому число классов равно 28. Обозначим через an число различных троек цифр с суммой Легко видеть, что число счастливых билетов, сумма первых трёх цифр которых Для вычисления значений an попробуем подсчитать сначала число одно- и двузначных чисел с суммой Смысл у этого многочлена следующий: коэффициент при sn в многочлене A1 равен числу однозначных чисел, сумма цифр которых Другими словами, коэффициент при sn в многочлене A1 равен 1, если Выпишем теперь многочлен Нетрудно видеть, что степень многочлена A2 равна 18. Действительно, 18 — наибольшая возможная сумма цифр двузначного числа. Несложно сосчитать и первые несколько коэффициентов этого многочлена: Оказывается, многочлен A2 легко строится по многочлену A1. ПРЕДЛОЖЕНИЕ 1. ДОКАЗАТЕЛЬСТВО. Произведение мономов sk и sm даёт вклад в коэффициент при мономе sn многочлена Теперь нетрудно выписать и многочлен ПРЕДЛОЖЕНИЕ 2. ДОКАЗАТЕЛЬСТВО. Доказательство практически дословно совпадает с доказательством предыдущего утверждения: коэффициент при sn в многочлене Итак, задача о числе счастливых билетов свелась к следующему: надо подсчитать число p0 — сумму квадратов коэффициентов многочлена Обратите внимание на то, что умножение на многочлен Однако можно не останавливаться на достигнутом и пойти дальше. Подставим вместо s выражение Воспользовавшись тем, что
2π получим
2π 2π Суммируя геометрическую прогрессию и пользуясь тем, что 2i получаем 1 – eiφ eiφ/2 sin(φ/2) откуда искомая величина равна
2π sin2 (φ/2) π sin φ Попробуем оценить значение интеграла (1). График функции sin φ Основная же составляющая интеграла (1) сосредоточена на отрезке при √33t Полагая 3√11π Полученный результат с хорошей точностью (отклонение составляет не более 3%) приближает искомое значение *. На основании рассмотренного примера можно сделать некоторые выводы о комбинаторных задачах и методах их решения.
Задачи перечислительной комбинаторики состоят в подсчёте числа объектов, принадлежащих некоторому семейству конечных множеств. У каждого множества семейства имеется свой номер (в задаче о числе счастливых билетов таким номером была сумма цифр трёхзначного числа) .
Как правило, задача перечислительной комбинаторики «в принципе» разрешима: для каждого множества из семейства можно выписать все его элементы и таким образом узнать их число. Проблема, однако, состоит в том. чтобы найти «хорошее» решение, не требующее выписывания всех элементов изучаемых множеств.
Определить, что такое хорошее решение, довольно трудно. Зачастую можно лишь сравнить два решения и сказать, какое из них лучше.
При решении задач перечислительной комбинаторики очень полезно рассматривать производящие многочлены (или, более общо, производящие ряды). В нашем случае пользу принёс производящий многочлен A3. Операции с комбинаторными объектами очень естественно выражаются в терминах производящих функций. Так, переход от однозначных чисел с заданной суммой цифр к трёхзначным числам состоял просто в возведении производящего многочлена A1 Привлечение методов из смежных областей математики (например, из анализа) позволяет Как-то участникам Всесоюзной математической олимпиады во время отдыха
N1(k) =
ì
1, если k принимает значения от 0 до 9,
í
î
0 при других значениях k.
9
Nn(k) =
∑
Nn–1(k – l);
l=0
(*)
k n = 1 n = 2 n = 3 n = 4 0 1 1 1 1 1 1 2 3 4 2 1 3 6 10 3 1 4 10 20 4 1 5 15 35 5 1 6 21 56 6 1 7 28 84 7 1 8 36 120 8 1 9 45 165 9 1 10 55 220 10 9 63 282 11 8 69 348 12 7 73 415 13 6 75 480 14 5 75 540 15 4 73 592 16 3 69 633 17 2 63 660 18 1 55 670 19 45 660 20 36 633 21 28 592 22 21 540 23 15 480 24 10 415 25 6 348 26 3 282 27 1 220 28 165 29 120 30 84 31 56 32 35 33 20 34 10 35 4 36 1
для двузначных номеров C = 10,
для четырехзначных C = 670,
для шестизначных C = 55 252,
для восьмизначных C = 4 816 030.
C ≈
102n
.

Н. Я. Виленкин
Счастливые
троллейбусные билеты
(
n
k)
=
n!
(1 + x + ... + xm–1)n =
∑
Cm(n, N) xN.
N
(1 + x + ... + xm–1)n =
(1 – xm)n
= (1 – xm)n (1 – x)–n.
n
∞
(1 – xm)n =
∑
(–1)k
(
n
k)
xmk, (1 – x)–n =
∑
(
k+n–1
n–1)
xk,
k=0
k=0
Cm(n, N) =
∑
(–1)k
(
n
k)(
n+N–km–1
n–1)
,
k
(*)
2
C10(6, 27) =
∑
(–1)k
(
6
k)(
32–10k
5)
=
k=0
=
(
32
5)
–
(
6
1)(
22
5)
+
(
6
2)(
12
5)
= 55 252.

Интегралом —
по счастливым билетам!
 Много ли счастливых билетов? Часто ли они попадаются?
Много ли счастливых билетов? Часто ли они попадаются?
π
C2n =
1
∫
(
sin 10x
)
2n
dx.
0
(1)
k
Nn(k) =
∑
Nn–1(l).
l=k–9
Nn(k + 1) – Nn(k) = Nn–1(k + 1) – Nn–1(k – 9).
(2)
Nn(0) = 1
(2')
N1(k) =
ì
1, если 0 ≤ k ≤ 9,
í
î
0, если k < 0 или k > 9.
(2")
C2n = N2n(9n).
(3)
π
Nn(k) =
1
∫
(
sin 10x
)
n
cos(9n – 2k)x dx.
0
(4)
Nn(k) = Nn(k).
(5)
π
1
∫
(
sin 10x
)
n
[cos(9n – 2k – 2)x – cos(9n – 2k)x] dx =
0
π
=
1
∫
(
sin 10x
)
n–1
[cos(9n – 9 – 2k – 2)x – cos(9n – 9 – 2k + 18)x] dx,
0
π
1
∫
(
sin 10x
)
n–1
[
sin 10x
{cos(9n – 2k – 2)x –
0
– cos(9n – 2k)x} – {cos(9n – 2k – 11)x – cos(9n – 2k + 9)x}] dx = 0,
 Таким образом, рекуррентное соотношение (2) для
Таким образом, рекуррентное соотношение (2) для
π
C2n, m =
1
∫
(
sin mx
)
2n
dx.
0

Снова о счастливых билетах
π
C6, 10 =
1
∫
(
sin 10x
)
6
dx.
0
(1)
π
C2n, m =
1
∫
(
sin mx
)
2n
dx.
0
N–1
C2n, m =
1
∑
f (xk), где xk =
a +
kπ
, f (x) =
(
sin mx
)
2n
.
k=0
(2)
(
sin mx
)
2n
n0
f (x) =
∑
(ak cos kx + bk sin kx);
k=0
π
N–1
1
∫
f (x) dx =
1
∑
f
(
a +
kπ
)
0
k=0
1
+
1
= 12.
f (x) =
(1 – xm)2n
= (1 – xm)2n (1 – x)–2n.
m
(1 + t)m =
∑
(
m
k)
tk,
k=0
(
m
k)
=
ì í î
m!
при 0 ≤ k ≤ m,
0
при 0 ≤ m < k.
(
–m
k)
= (–1)k
(
m + k – 1
k)
.
[n – n/m]
C2n, m =
∑
(–1)k
(
2n
k)(
(n – k)m + n – 1
2n – 1)
,
k=0
(3)
C6, 10 =
(
6
0)(
32
5)
–
(
6
1)(
22
5)
+
(
6
2)(
12
5)
= 201 376 – 6 · 26 334 + 15 · 792 = 55 252.
C2n, 2 =
(
2n
n)
.

фрагменты классической математики
С. К. Ландо
a0 = 1 (есть всего одна тройка цифр 000 с суммой 0); a1 = 3 (есть три тройки 001, 010, 001 с суммой цифр 1); a2 = 6 (тройки 002, 020, 200, 011, 101, 110).
2π
1
∫
eikφ · e–imφ dφ =
0
ì
1, k = m,
í
î
0, k ≠ m,
2π
2π
27
27
27
1
∫
| A3(eiφ)|2 dφ =
1
∫
∑
ak eikφ ·
∑
am e–imφ dφ =
∑
ak2.
0
0
k=0
m=0
k=0
eiφ – e–iφ
= sin φ,
A1(eiφ) = 1 + eiφ + ... + e9iφ =
1 – e10iφ
=
e5iφ sin(5φ)
,
2π
π/2
p0 =
1
∫
(
sin2 (5φ)
)
3
dφ =
1
∫
(
sin 10φ
)
6
dφ.
0
–π/2
(1)
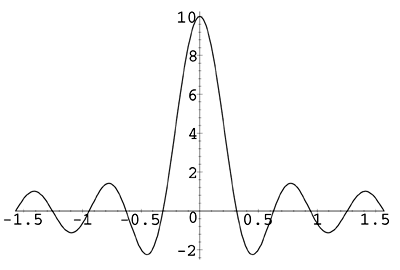
Вид графика функции f (φ) = sin(10φ) .
π/10
π/10
∫
f t dφ =
∫
et ln f dφ
–π/10
–π/10
π/10
π/10
∫
et(ln 10 – 33φ²/2) dφ = et ln 10
∫
e–33tφ²/2 dφ ≈ et ln 10
√2π
.
–π/10
–π/10
p0 ≈
106
≈ 56 700.
*