| В МИРЕ НАУКИ Scientific American · Издание на русском языке № 8 · АВГУСТ 1983 · С. 76–86 |
ДЖОЗЕФ У. ДАУБЕН
| В МИРЕ НАУКИ Scientific American · Издание на русском языке № 8 · АВГУСТ 1983 · С. 76–86 |
Природа бесконечности всегда была предметом спора. О том, что она интересовала ещё древних мыслителей, свидетельствуют знаменитые парадоксы Зенона Элейского, который доказывал, что движение мыслить невозможно, поскольку движущийся объект проходит бесконечное число точек в конечное время. Разработанное Ньютоном в XVII в. исчисление бесконечно малых позволило
Сущность трудов Кантора хорошо известна: разработав то, что он назвал арифметикой трансфинитных чисел, он придал математическое содержание идее актуальной бесконечности. При этом он заложил основы теории абстрактных множеств и внёс существенный вклад в основание анализа и в изучение континуума вещественных чисел. Самое замечательное достижение Кантора состояло в доказательстве того, что не все бесконечные множества количественно эквивалентны, т.е. имеют одинаковую мощность, а потому их можно сравнивать друг с другом. Например, множество точек прямой и множество всех рациональных чисел являются бесконечными. Кантор сумел доказать, что мощность первого множества превосходит мощность второго. Идеи Кантора оказались столь неожиданными и противоречащими интуиции, что знаменитый французский математик Анри Пуанкаре назвал теорию трансфинитных чисел «болезнью», от которой математика должна
Известно также, что Кантор был подвержен «нервным заболеваниям», участившимся с возрастом и всё более ослаблявшим его. Эти расстройства были,
Такие представления искажают истину, сводя к тривиальности действительные интеллектуальные устремления непредвзято мыслящих противников канторовской теории. Они также умаляют силу и широту защиты Кантором своих идей. Сначала он воздерживался от введения трансфинитных чисел, считая, что идею актуальной бесконечности нельзя сформулировать непротиворечиво, а потому ей не место в строгой математике. Однако, по его собственному свидетельству, он вскоре преодолел своё «предубеждение» в отношении трансфинитных чисел, ибо понял, что без них нельзя построить теорию бесконечных множеств. Собственные первоначальные сомнения позволили Кантору предвосхитить оппозицию с разных сторон и вооружиться как философскими и теологическими, так и математическими аргументами. Более того, отстаивая свою теорию, он сумел придать идеям, лежащим в её основе, значительную силу.
Георг Фердинанд Людвиг Филипп Кантор родился 3 марта 1845 г. в России, в
Когда Кантор был ещё ребёнком, семья переехала из России в Германию, и именно там началось его обучение математике. Защитив в 1868 г. диссертацию по теории чисел, он получил степень доктора в Берлинском университете. Два года спустя он занял должность
 |
Фотография Кантора и его жены (примерно 1880 г.). К этому времени его работы уже получили известность. В одной из них он доказал, что бесконечное множество действительных чисел, представленное континуумом точек на прямой, больше бесконечного множества всех рациональных чисел. Он показал также, что можно определить бесконечные величины, названные трансфинитными числами, которые описывают такое различие. Через несколько лет после того, как был сделан этот снимок, Кантор испытал сильный приступ маниакально-депрессивного психоза, который в конце концов положил конец его творческому пути в математике. Оригинал этой фотографии находится в частной коллекции Эгберта Шнайдера. |
Проблема, подсказанная Гейне, проистекает из трудов французского математика Жана Батиста Жозефа Фурье. В 1822 г. Фурье показал, что график любой «достаточно гладкой» кривой (т.е. кривой, имеющей максимум конечное число точек разрыва) может быть представлен всюду на интервале в виде суммы некоторого бесконечного тригонометрического ряда. Другими словами, накладывая друг на друга бесконечное число синусоидальных и косинусоидальных колебаний, каждую точку на этой «достаточно гладкой» кривой, за исключением точек разрыва, можно аппроксимировать с любой требуемой степенью точности [см. рисунок ниже]. Говорят, что такой ряд сходится к кривой или функции, за исключением конечного числа точек, или же сходится «почти всюду». Результат Фурье имел большое значение, поскольку он указывал, что некоторые сложные функции могут быть представлены в виде суммы синусов или косинусов, с которыми легче оперировать математически. Однако, чтобы оправдать такую замену, требовалось доказать, что к функции сходится только один такой тригонометрический ряд. Условия, при которых сходящийся к функции тригонометрический ряд является единственным, и начал исследовать Кантор.
В 1870 г. Кантор доказал, что если функция непрерывна всюду на интервале, то её представление тригонометрическим рядом единственно1. Его следующий шаг состоял в ослаблении требования непрерывности функции всюду на интервале2. Предположим, например, что график аппроксимируемой функции представляет собой прямую, параллельную оси x, за исключением точки
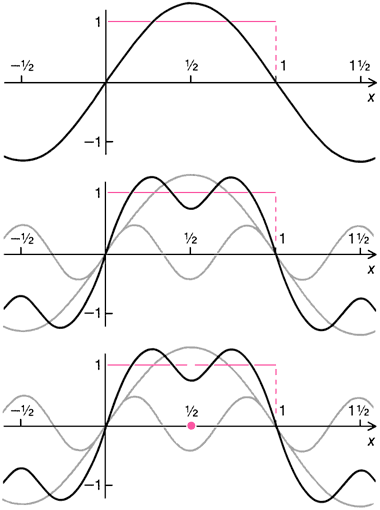 |
Гладкий непрерывный график, ординаты точек которого зависят от значений соответствующих точек на оси x, можно с любой требуемой точностью аппроксимировать тригонометрическим рядом, т.е. суммой синусов и косинусов. Например, прямая горизонтальная линия, отстоящая на единицу длины вверх от оси x (цветная), может быть аппроксимирована наложением синусоидальных колебаний (серые кривые); изображены две первые стадии аппроксимации (чёрные кривые наверху и в середине). Тригонометрический, аппроксимирующий график является единственным. Однако, даже если график не непрерывен, его часто можно аппроксимировать единственным тригонометрическим рядом. Например, если ординаты точек графика равны всюду единице, за исключением точки |
В 1872 г. Кантор публикует работу, представляющую собой важнейшее открытие. Стремясь к более общей формулировке теоремы единственности, он доказал, что если исключительные точки распределены на оси x некоторым специальным образом, то их может быть и бесконечно много. Установить это можно было только на основе точного описания бесконечного множества исключительных точек. Однако для этого, как понимал Кантор, необходим более глубокий анализ континуума точек на оси x. Так, исследуя сходимость тригонометрических рядов, Кантор постепенно начинает сосредоточивать своё внимание на соотношении точек в континууме.
Кантор принял за аксиому, что всякой точке непрерывной линии соответствует некоторое число, которое он назвал действительным числом, чтобы отличить его от «мнимых» чисел, кратных
Основную трудность в теории действительных чисел представляют такие числа, как π и √2, не являющиеся рациональными. (Рациональное число — это такое число, которое можно выразить в виде частного двух целых чисел. Ещё в античности было известно, что √2, √3, √5 и многие другие корни являются иррациональными.) Так как правомерность рациональных чисел не вызывала сомнений, Кантор пошёл по пути, указанному Карлом Вейерштрассом, одним из его бывших учителей в Берлинском университете. Кантор предположил, что всякое иррациональное число может быть представлено бесконечной последовательностью рациональных чисел. Например, число √2 можно представить бесконечной последовательностью рациональных чисел 1; 1,4;
Несмотря на преимущества канторовского подхода, некоторые математики приняли его как вызов, поскольку он предполагал существование множеств или последовательностей чисел, имеющих бесконечно много элементов. Философы и математики отвергали концепцию завершённых бесконечностей со времён Аристотеля главным образом вследствие тех логических парадоксов, к которым, как казалось, они приводят. Например, Галилей указывал, что если в математике принять бесконечные завершённые множества, то чётных чисел должно быть столько же, сколько чётных и нечётных вместе. Всякому чётному числу можно сопоставить целое число, равное половине его величины, таким образом налицо взаимно однозначное соответствие между элементами того и другого множества. Некоторые теологи, например Фома Аквинский, также были против идеи завершённой бесконечности, считая её прямым вызовом единой и абсолютно бесконечной природе бога.
Чтобы избежать подобные возражения, математики стремились проводить чёткое различие между бесконечностью, рассматриваемой как завершённая величина, и бесконечностью, рассматриваемой как потенциальная, т.е. представляемой неопределённой суммой или рядом членов, стремящихся к некоторому пределу. Правомерной они считали лишь потенциальную бесконечность. В 1831 г. своё отношение к завершённым бесконечностям Карл Фридрих Гаусс выразил словами, которые Кантор однажды назвал слишком категорическими. В письме Генриху Шумахеру Гаусс писал: «Что касается Вашего доказательства, я прежде всего протестую против применения бесконечной величины как завершённой, в математике это никак не допустимо. Понятие бесконечности есть лишь способ выражения понятия предела».
Говоря о пределах, можно было избежать парадоксов, связанных с актуальными бесконечностями. Например, прибавляя дополнительные цифры к десятичному разложению числа π, можно аппроксимировать истинное значение π с возрастающей точностью. Однако Гаусс утверждал, что все члены десятичного разложения числа π не могут быть даны. Действительно, для точного определения π требовалось бы взять бесконечное число членов как
Кантор не был одинок в изучении свойств континуума. В 1872 г., когда появилась его вышеуказанная статья, немецкий математик Рихард Дедекинд тоже опубликовал анализ континуума, основанный на бесконечных множествах. В своей работе Дедекинд явно высказал идею, позднее уточнённую Кантором: «Прямая бесконечно более богата индивидуумами-точками, чем область... рациональных чисел индивидуумами-числами». Сказанное можно представить следующим образом. Если на отрезке прямой рассмотреть распределение точек, соответствующих рациональным числам, то сколь бы малым ни был этот отрезок, на нём имеется бесконечно много рациональных точек. Суть идеи Дедекинда состояла в том, что, несмотря на плотность рациональных точек на отрезке прямой, на нём всё же найдётся место, чтобы вставить бесконечное число иррациональных точек. Такая иррациональная точка, как √2, попадает между рациональными точками, и таким образом множество рациональных чисел, хотя оно и всюду плотно, всё же разрежено, имеет «щели» и не является непрерывным.
Утверждение Дедекинда верно отражало суть понятия континуума, за исключением одного важного аспекта. Взяв идеи Дедекинда за основу, нельзя установить, насколько бесконечное множество точек континуума превышает бесконечное множество рациональных точек. Великий вклад в решение этого вопроса был сделан Кантором, когда он в 1874 г. опубликовал свою статью «Об одном свойстве совокупности всех действительных алгебраических чисел» в «Журнале чистой и прикладной математики» Августа Леопольда Крелле, называемом также журналом Крелле, — наиболее авторитетном среди математиков периодическом издании того времени.
Фактически Кантор воспользовался указанным Галилеем парадоксом и превратил его в средство количественного сравнения бесконечных множеств. Он назвал два множества эквивалентными, если между элементами этих множеств можно установить взаимно однозначное соответствие. Предположим, у нас имеется ведёрко, заполненное чёрными и цветными шариками. Каким образом можно сравнить количество чёрных и цветных шариков? Простейший способ состоит в извлечении шариков из ведёрка парами, состоящими из чёрного и цветного шариков. Если каждый шарик может быть объединён в пару с шариком другого цвета, то два множества эквивалентны. Если нет, то оставшиеся в ведёрке шарики показывают, каких шариков было больше.
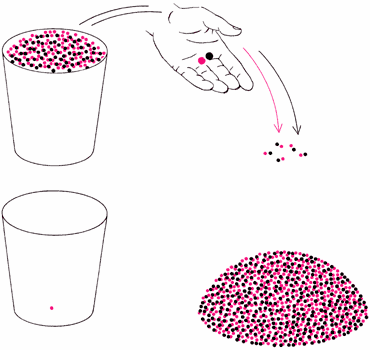 |
Два множества можно сравнивать по величине, сопоставляя элементы одного множества с элементами другого. Например, чтобы определить, каких шариков в ведёрке больше: цветных или чёрных, можно брать их из ведёрка парами, состоящими из цветного и чёрного шариков, до тех пор, пока там не останутся шарики одного цвета. Именно этот остаток и указывает, каких шариков было больше. Такой же принцип Кантор применил для количественного сравнения бесконечных множеств. |
Используя принцип взаимно однозначного соответствия, Кантор показал, что свойство, которое Галилей рассматривал как парадоксальное, фактически является естественным свойством бесконечных множеств. Множество чётных чисел эквивалентно множеству всех целых положительных чисел, чётных и нечётных, вместе взятых, поскольку объединение в пары элементов каждого из этих множеств может быть осуществлено без опущения
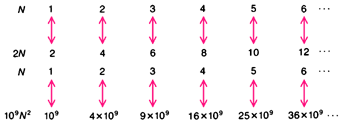 |
Целые числа можно одно за другим объединить в пары с чётными числами, не исчерпав |
Кантор также предложил оригинальный способ объединения элементов множества всех рациональных чисел в пары с целыми числами [см. нижний рисунок].
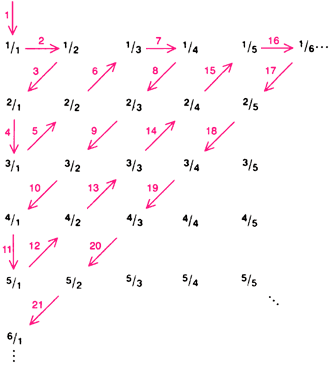 |
Бесконечное множество рациональных чисел (т.е. чисел, которые можно представить как частное двух целых чисел) могло бы показаться значительно бóльшим, чем множество целых чисел. Например, между двумя любыми соседними целыми числами, допустим 0 и 1, имеется бесконечно много рациональных чисел. Тем не менее в 1874 г. Кантор показал, что рациональные числа можно одно за другим объединить в пары с целыми числами. Всякое рациональное число можно разместить в квадратной таблице, как показано на рисунке. Тогда каждое из них может быть связано с целым числом путём проведения цветной линии. Таким образом, множество рациональных чисел является счётным. |
Всякое множество чисел, элементы которого можно расположить один за другим или фактически сосчитать, используя множество целых положительных чисел, Кантор назвал счётным множеством.
При данной плотности рациональных чисел на прямой и относительной «разреженности» целых чисел, может показаться крайне противоречащим интуиции то, что эти два множества оказываются количественно эквивалентными. Однако Кантор пошёл ещё дальше. Он доказал, что взаимно однозначного соответствия между множеством целых чисел и множеством всех точек на прямой, т.е. множеством действительных чисел, быть не может; одним словом, действительные числа образуют несчётное множество. Кантор дал довольно сложное доказательство этого утверждения в своей статье, опубликованной в 1874 г. Я не буду останавливаться на нём, а изложу основную идею гораздо более простого, но более мощного способа доказательства, предложенного им в 1891 г.
Кантор начал своё доказательство с предположения, что существует взаимно однозначное соответствие между множеством действительных чисел и множеством целых чисел. Последующим рассуждением показывается, что это предположение приводит к противоречию, отсюда следует, что первоначальное предположение неверно и такое взаимно однозначное соответствие невозможно. Рассуждение можно упростить, рассматривая только множество действительных чисел, заключённых между 0 и 1. Если это множество больше множества целых чисел, то множество всех действительных чисел и подавно больше него.
Итак, предположим, что действительные числа, заключенные между 0 и 1, могут быть одно за другим объединены в пары с целыми числами. Установление такого соответствия эквивалентно составлению некоторого перечня действительных чисел, каждое из которых представляется как бесконечная десятичная дробь. Тогда можно определить новое действительное число,не включённое в этот перечень. Берём первую цифру первого десятичного разложения в указанном перечне действительных чисел. Если эта цифра равна 1, то пишем 9 на первом месте после запятой. Если первая цифра в этом перечне не равна 1, то на первом месте определяемого числа пишем 1. Построение нашего нового числа продолжается путём изменения второй цифры второго десятичного разложения в перечне, третьей цифры в третьем десятичном разложении и так далее. Вновь построенное число должно отличаться по крайней мере одним десятичным знаком от каждого действительного числа, содержащегося в перечне, однако оно тем не менее представляет собой некоторое действительное число, расположенное между 0 и 1. Поэтому можно построить некоторое число, не содержащееся в перечне действительных чисел, и таким образом предположение, что все действительные числа можно пересчитать, приводит к противоречию.
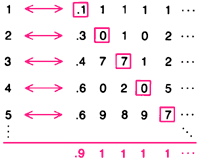 |
Множество действительных чисел, представленное континуумом точек на прямой, не является счётным. Если бы оно было счётным, то действительные числа, скажем между 0 и 1, можно было бы одно за другим объединить в пары с целыми числами. Всякое действительное число в перечне можно представить бесконечным десятичным разложением (такие бесконечные десятичные дроби, как |
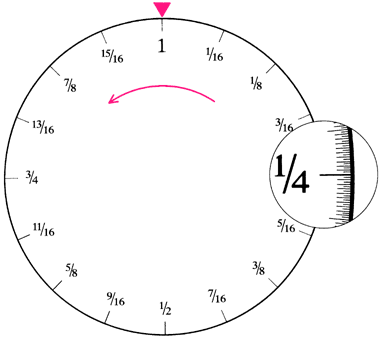 |
Вероятность случайного выбора точки, представляющей рациональное число, из континуума действительных чисел показывает, как множество рациональных чисел сравнивается по величине с множеством действительных чисел. Вероятность есть отношение числа рациональных точек к общему числу точек на некотором интервале. Здесь интервал между 0 и 1 представлен окружностью свободно вращающегося колеса (на этом колесе 0 и 1 отождествляются). Предполагается, что вероятность остановки колеса в любой точке одинакова. Точки, представляющие рациональные числа, бесконечно плотны в том смысле, что вдоль любой сколь угодно короткой дуги между двумя рациональными точками на окружности должно находиться бесконечное число рациональных точек. Несколько таких точек помечено. Тем не менее множество всех точек на окружности бесконечно больше множества рациональных точек: вероятность, что колесо остановится в рациональной точке, равна нулю. Точнее эта вероятность меньше любой сколь угодно малой величины. |
В августе 1874 г. Кантор женился на Валли Гутман. Супруги провели конец лета в горах Гарца, где они встретились с Дедекиндом. Этот период оказался чрезвычайно плодотворным для Кантора. Несколько раньше в одном из своих писем Дедекинду Кантор писал: «Можно ли сопоставить поверхность (например, квадратную площадку, включая её границы) с отрезком прямой (включающим свои концы) таким образом, чтобы каждой точке поверхности соответствовала одна точка на этом отрезке, и наоборот?» Кантор полагал, что ответ должен быть отрицательным, но это требовало доказательства.
Однако в 1877 г. Кантор сообщает Дедекинду о своём поразительном результате: вопреки мнению, распространённому среди математиков, ему удалось доказать, что взаимно однозначное соответствие между точками прямой и точками плоскости возможно. Доказательство состояло в представлении каждой точки квадрата парой десятичных дробей. Эти десятичные представления «перемешиваются» строго определенным образом, чтобы получить одно десятичное разложение, и эта десятичная дробь сопоставляется с точкой на отрезке прямой. Весь этот процесс обратим [см. рисунок ниже]. Слова Кантора: «Я вижу это, но никак не могу этому поверить!» — говорят о том, насколько этот результат оказался неожиданным для него самого.
Кантор сразу же подготовил рукопись с описанием своего нового открытия, и послал её в журнал Крелле. Работа эта послужила первым поводом для открытых столкновений между её автором и Кронекером. Будучи редактором журнала, Кронекер имел право отказать в публикации любой статьи, работа же Кантора настолько шокировала его, что он не преминул этим правом воспользоваться. Несмотря на то что Кантор представил свою рукопись 12 июля, для подготовки её к публикации ничего не делалось, и она не появилась в журнале в 1877 г. Подозревая вмешательство Кронекера, Кантор пишет Дедекинду письмо, сетуя на неблагоприятное отношение к его рукописи. В письме он говорит также о своём желании забрать её из редакции. Однако Дедекинд, рассказав Кантору о собственном опыте в подобных делах, убедил его подождать, и оказался прав — статья наконец появилась в томе за 1878 г. Однако Кантор был настолько огорчён этим инцидентом, что отказался впредь публиковаться в журнале Крелле.
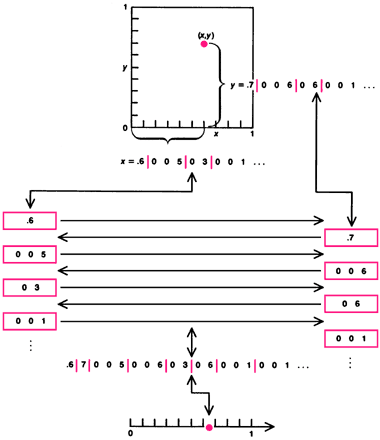 |
Между точками плоскости и точками прямой можно установить взаимно однозначное соответствие. Каждая точка плоскости представляется парой бесконечных десятичных дробей и эти бесконечные дроби разбиваются на группы. Каждая цифра десятичного разложения, кроме нуля, начинает новую группу. Затем эти группы комбинируются и превращаются в одну бесконечную десятичную дробь, представляющую точку на плоскости. Вся процедура обратима. Аналогичное рассуждение показывает, что число точек любого конечномерного пространства эквивалентно числу точек на линии. |
Полемика между Кантором и Кронекером усугублялась личной враждебностью, однако её причиной было различие во взглядах на обоснование математики. Подобные различия во взглядах и сейчас находят отражение в споре между сторонниками конструктивистской и формальной математики. Кронекер, сторонник конструктивизма, хорошо известен своим высказыванием, резюмирующим сущность его позиции: «Бог создал целые числа; всё остальное — дело рук человеческих». В этом духе он защищал построение всей математики из целых чисел и их конечных арифметических комбинаций. В начале
Кантор, написавший две большие статьи под руководством Кронекера в свои студенческие годы в Берлинском университете, хорошо знал эту крайнюю позицию Кронекера и в
Определение иррациональных чисел, данное Кантором в статье, опубликованной в 1874 г., было равносильно принятию существования завершённых бесконечных множеств. Кантор занял позицию формальной математики в вопросе существования иррациональностей и утверждал, что единственным основанием их законности в математике является их формальная и внутренняя непротиворечивость. «При введении новых чисел, — писал он однажды, — от математика требуется только дать им определения, которые позволят... отличать их друг от друга. Как только число удовлетворяет этим условиям, оно может и должно рассматриваться как существующее и реальное в математике».
Эта точка зрения на иррациональные числа оказалась решающей для оправдания Кантором введения трансфинитных чисел. В статье, опубликованной в 1872 г., он определил множества исключительных точек, введя понятие предельной точки. Например, иррациональное число √2 представляет собой предельную точку последовательности 1; 1,4;
Для данного бесконечного множества P Кантор определил производное множество P1 как множество всех предельных точек P. Аналогично, если P1 также является бесконечным множеством, то его производное множество P2 можно определить как множество всех предельных точек множества P1. Кантор показал, что отношение включения определяет естественное упорядочение для множеств: оказывается, что всякий элемент множества P2 является и элементом множества P1, и, таким образом, P2 является подмножеством P1; аналогично P3 является подмножеством P2 и так далее.
Может оказаться, что для некоторого конечного целого числа n производное множество Pn представляет собой конечное множество. Если это условие выполняется, то бесконечное множество P, порождающее Pn, есть в точности множество исключительных точек, которое позволяет доказать достаточно общий вариант канторовской теоремы о единственности представления функций тригонометрическими рядами. С другой стороны, может также оказаться, что никакое множество в последовательности P1, P2,
Кантор мог бы добавить, что индексы ∞, ∞+1,
Как указывал Кантор, непосредственным поводом для введения этих чисел было то, что они оказались необходимыми для дальнейшего развития теории множеств и изучения действительных чисел. Тем не менее, чтобы ответить критикам вроде Кронекера, Кантор отстаивал правомерность этих чисел в математике и со своей философской позиции: как только непротиворечивость трансфинитных чисел признана, их уже нельзя отвергать, как и другие принятые, но сразу же поставленные под сомнение числа вроде иррациональных. Формулируя теорию бесконечности, дающую возможность избежать известные математические парадоксы, Кантор верил, что он устранит единственно обоснованное возражение, которое могли выдвинуть математики против узаконивания понятия завершённой бесконечности.
Трансфинитные числа, введённые в конце концов Кантором, широко известны в обозначении, которое он принял для них позже: в виде буквы
Ординальное число определяется его порядком или положением в некотором перечне. Ординальное число, ассоциируемое с конечным множеством, соответствует кардинальному числу этого множества. Например, всякое множество, состоящее из пяти элементов (т.е. всякое множество, кардинальное число которого равно пяти), можно в некотором роде мыслить как непосредственно следующее за любым множеством из четырёх элементов. Другими словами, ординальное число этого множества тоже равно пяти; оно является пятым множеством в перечне множеств. Однако ординальное число бесконечного множества следует отличать от его кардинального числа. Кантор показал, что можно построить бесконечное число бесконечных множеств, имеющих различные ординальные числа, но одно и то же кардинальное число. Фактически Кантор позднее сумел превратить это свойство бесконечных множеств в критерий отличия их от конечных множеств: множество конечно, если его кардинальное и ординальное числа совпадают.
Кантор показал, что ординальное число последовательности конечных множеств возрастающей величины 1, 2,
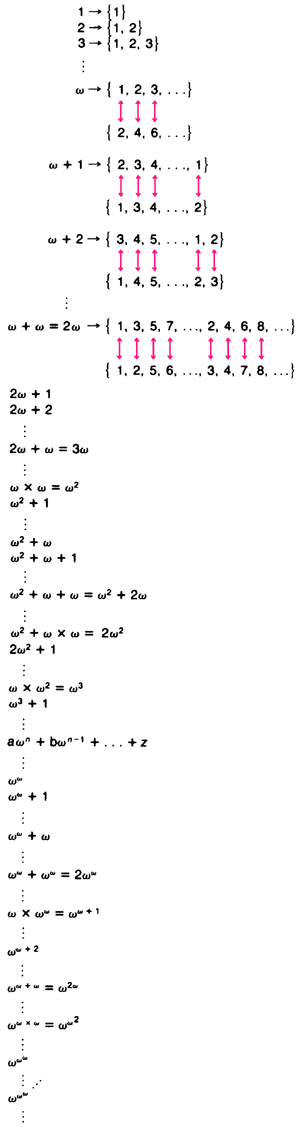 |
Трансфинитные ординальные числа определяются их порядком или положением в некотором перечне. Этот перечень порождается в соответствии с двумя принципами. |
Каким образом можно провести различие, скажем, между ординальными числами ω и ω+1. Различие определяется порядком элементов в множествах, которым соответствуют ω и ω+1. Например, множество натуральных чисел в их известной последовательности (1, 2,
Определив трансфинитные ординальные числа, Кантор приступил к описанию их арифметических свойств. Между трансфинитными и обычными числами следует провести важное различие в отношении свойства коммутативности для сложения и умножения. Для двух обычных чисел A и B свойство коммутативности выражает тот факт, что A+B равно B+A и A×B равно B×A. Однако, что касается трансфинитных чисел, свойство коммутативности уже не может быть гарантировано. Например, ω+2, представляющее последовательность (1, 2,
Хотя различие между ординальным и кардинальным числом для конечных множеств не является характерным, оно помогает объяснить, как применение понятия числа к бесконечным множествам может привести к путанице и парадоксам. Поскольку понятия ординального и кардинального числа для бесконечных множеств существенно различны, то при рассмотрении числа, ассоциированного с бесконечным множеством, всякое рассуждение, не учитывающее это различие, может привести к неясности. Таким образом, на бесконечные множества нельзя распространять кажущиеся очевидными свойства конечных множеств, как это делали Галилей и другие.
Несмотря на значительные результаты, полученные Кантором в
Эта догадка известна как гипотеза континуума Кантора и никогда не была доказана. В 1963 г. П. Дж. Коэн из Станфордского университета, опираясь на работу Курта Гёделя и математиков из Института высших исследований, показал, что, хотя эта гипотеза не противоречит аксиомам общепринятой теории множеств, она вместе с тем и не зависит от них. Фактически роль гипотезы континуума в теории множеств такая же, как роль евклидовского постулата параллельности в геометрии. При допущении истинности или ложности гипотезы континуума можно построить различные версии теории множеств точно так же, как при допущении истинности или ложности аксиомы параллельности можно строить евклидову или неевклидовы геометрии (см. П. Дж. Коэн, Р. Херш «Неканторовская теория множеств», Scientific American, декабрь, 1967 г.4).
Кантору тяжело было сознавать безуспешность своих усилий доказать континуум-гипотезу, что явилось,
Вскоре после этого, в мае 1884 г., Кантор испытал серьёзное нервное расстройство. Осознание неудачи в решении проблемы континуума и нападки Кронекера могли способствовать этому срыву. Однако эти отрицательные факторы, конечно, не были причиной его болезни, которая прогрессировала очень быстро. В конце июня 1884 г. после «выздоровления» и наступления фазы депрессии Кантор жаловался на упадок сил и потерю интереса к занятию математикой. Он довольствовался лишь выполнением незначительных административных обязанностей в университете и не чувствовал себя способным на большее.
Хотя Кантор порой возвращается к математике, его всё более увлекают другие интересы. Начав изучать английскую историю и литературу, он становится участником спора, который вели в то время многие учёные, — спора относительно предположения, что автором шекспировских пьес был Френсис Бэкон. Кантор пытался, но безуспешно преподавать философию вместо математики и начал переписываться с некоторыми теологами, проявившими интерес к философским выводам из его теории бесконечности. Эта переписка имела особое значение для Кантора, так как он был убеждён, что идея трансфинитных чисел была ниспослана ему богом. Он очень хотел, чтобы его идеи были изучены теологами с целью согласования его концепции бесконечного с церковным учением.
Важно отметить, что Кантор способствовал созданию профессионального объединения — Немецкого математического общества, назначение которого состояло в содействии развитию математики в Германии. Он считал, что его научная карьера пострадала от предубеждённого отношения к его трудам, и надеялся, что независимая организация позволит молодым математикам самостоятельно судить о новых, возможно, радикальных идеях и побудит их заняться этими идеями.
Последним элементом теории бесконечных множеств, который оставался ещё «не доработанным», был вопрос о природе и статусе трансфинитных кардинальных чисел. Эволюция мыслей Кантора относительно этого предмета любопытна, поскольку трансфинитные кардинальные числа были той завершающей частью его теории, которой нужно было дать строгое определение и присвоить специальный символ. Сейчас трудно с полной ясностью представить ту неизвестность, в которой продвигался вперёд Кантор. До сих пор я описывал его работы, как если бы он уже пришёл к выводу, что мощность бесконечного множества можно определять как кардинальное число. Фактически, хотя Кантор понимал, что именно мощность множества указывает на его эквивалентность (или неэквивалентность) любому другому множеству, он первоначально избегал предположения, что мощность бесконечного множества можно интерпретировать как некоторое число.
Эти два понятия Кантор начал отождествлять в сентябре 1883 г.; однако всё ещё не было символа, позволяющего отличать одно трансфинитное число от другого. Так как он уже принял символ ω для обозначения наименьшего трансфинитного ординального числа, то ясно, что ординальные числа были значительно более важными, чем кардинальные, для раннего концептуального развития канторовской теории множеств. Решив ввести символ для обозначения первого трансфинитного кардинального числа, Кантор заимствовал его из символов, уже использовавшихся для обозначения трансфинитных чисел: первое трансфинитное кардинальное число было записано в
Кантор не пользовался алефами в качестве символов до 1893 г. Примерно в это время итальянский математик Джулио Виванти готовил общее изложение теории множеств, и Кантор понимал, что необходимо принять стандартные обозначения. Для обозначения трансфинитных кардинальных чисел он выбрал алефы, считая, что известные греческие и римские алфавиты слишком широко использовались в математике. Выбранная буква א была доступна для набора в немецких типографиях. Этот выбор Кантор обосновывал ещё и тем, что еврейский алеф был одновременно символом
Последние значительные работы Кантора по теории множеств опубликованы в 1895 и 1897 гг. В докладе, прочтённом на первом заседании Немецкого математического общества в 1891 г., он доказал, что кардинальное число любого множества меньше кардинального числа множества всех его подмножеств. (Один из способов доказательства представлен на следующем рисунке.)
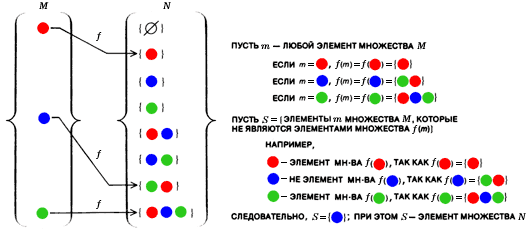 |
Бесконечная последовательность множеств, каждое из которых больше предшествующего ему в этой последовательности, может быть построена при рассмотрении всех подмножеств любого заданного множества. Канторовский диагональный метод показывает, что, допустив взаимно однозначное соответствие f между множеством M и множеством N всех его подмножеств, мы можем построить подмножество S, не включённое в это однозначное соответствие, каковым бы ни было f. Чтобы понять это построение, рассмотрим конечное |
Несколько лет спустя он получил такое следствие из этого результата: кардинальное число континуума равно кардинальному числу
Однако аргументы, использованные Кантором при доказательстве утверждения о кардинальном числе множества подмножеств, привели к существенно иным заключениям. Наиболее важное из них сделал Бертран Рассел в 1903 г.: он показал, что рассмотрение всех множеств, не включающих себя в качестве элементов, может привести к парадоксу в теории множеств. Этот вывод Рассела указывал на то, что канторовское определение множества нельзя считать удовлетворительным. Эта проблема стала одной из важнейших в математической логике XX столетия. Тем не менее ни один из канторовских результатов ещё не был опровергнут в трансфинитной арифметике.
Ещё до 1903 г. Кантор всё чаще испытывает приступы маниакальной депрессии, и нам неизвестно, познакомился он с указанной работой Рассела или нет. Болезнь вынудила Кантора просить в Университете в Галле разрешения на отпуск в течение осеннего семестра 1899 г. Его просьба была удовлетворена. В ноябре того же года он направил письмо министру культуры Германии о своём намерении полностью отказаться от профессуры. Поскольку его зарплата оставалась прежней, он готов был согласиться на скромную должность в библиотеке. Письмо заканчивалось требованием, чтобы министр сообщил свой ответ в ближайшие два дня. Если ему не предложат другую работу вместо преподавания, то, писал он, как человек, родившийся в России, он будет пытаться поступить на службу в русский дипломатический корпус.
По-видимому, ответ на просьбу Кантора не последовал, а на службу к императору Николаю II он не поступил. Тем не менее этот случай является характерным в поведении Кантора. Так, например, ещё в 1884 г., после первого серьёзного приступа болезни он всерьёз рассматривал вопрос об отказе от математики ради философии. В конце 1899 г. он был госпитализирован
Имеется в то же время определённая связь между болезнью Кантора и его научным творчеством. Некоторые документы говорят о том, что болезнь давала ему передышку от повседневных дел, которую он использовал для развития своих математических идей в уединении госпиталя или в спокойной обстановке дома. Возможно, болезнь также усиливала его веру, что идея трансфинитных чисел была внушена ему богом. После длительной госпитализации в 1908 г. он послал письмо одному из друзей в Гёттингене — математику Грейс Чисхольм Юнг, англичанке по происхождению. Как он писал, его маниакальная депрессия была побуждающим фактором: «Благодаря обстоятельствам судьбы, не только не сломившим меня, но фактически придавшим мне внутренней силы и сделавшим меня более счастливым и восприимчивым к радостям жизни, чем я был в последние годы, я оказался далеко от дома, можно сказать, далеко от мира... В этой длительной изоляции интерес к математике, в частности к теории трансфинитных чисел, не угасал во мне».
В другом письме Кантор выражает убеждённость в истинности своей теории в квазирелигиозных терминах: «Моя теория как скала; всякая стрела, направленная в эту скалу, тотчас же отскакивает от неё и устремляется к выпустившему её. Уверен я в этом потому, что изучил её со всех сторон за многие годы и рассмотрел все возражения, которые
Последующие поколения могли бы отмести эту философию, взять под подозрение его многочисленные ссылки на Фому Аквинского и на отцов церкви, пересмотреть метафизические заявления и полностью упустить из вида глубоко религиозные корни веры Кантора в абсолютную истинность его теории. Однако указанные обстоятельства сыграли свою роль в его решении не отбрасывать трансфинитные числа. Сопротивление, кажется, даже утвердило его решимость. Стойкость и убеждённость Кантора позволили теории трансфинитных множеств пережить годы сомнений и нападок и в конце концов вырасти в грандиозную революционизирующую силу в математике XX столетия5.
| 1. | Формулировка этого результата Кантора не вполне корректна. Его правильнее описать так: если функция действительного переменного задана сходящимся к ней тригонометрическим рядом в каждой точке, то такое её представление единственно. Здесь нет речи об условии непрерывности, поскольку произвольная непрерывная функция может привести к расходящемуся тригонометрическому ряду в одной или даже бесконечном множестве точек. назад к тексту |
| 2. | Кантор ослаблял требование сходимости ряда к значению функции в каждой точке. назад к тексту |
| 3. | На самом деле у Кантора речь шла не о точках разрыва, а о точках, в которых ряд расходится или не представляет значение функции, и именно такие точки он называл исключительными. назад к тексту |
| 4. | Имеется перевод: Природа, 1969, № 4, с. 43–55. назад к тексту |
| 5. | Следует отметить преувеличение автором роли теологических мотивов при создании и защите Кантором теории множеств. Теория множеств создавалась им на математической основе, причём более широкой, чем это раскрыто в публикуемой статье. Теологические мотивы стали появляться у Кантора в основном после того, как на построенную им теорию стали нападать философы и теологи; эти мотивы усиливались с развитием его болезни и отпадали в периоды относительного выздоровления. назад к тексту |
| 1. | Kurt Gödel. What is Cantor's continuum problem? In: Philosophy of Mathematics: Selected Readings (Edited by Paul Benacerraf and Hilary Putnam). Prentice-Hall, Englewood Cliffs, New Jersey, 1964. |
| 2. | Herbert Meschkowski. Probleme des unendlichen: werk und leben Georg Cantors. Vieweg, Braunschweig, 1967. |
| 3. | I. Grattan-Guinness. Towards a biography of Georg Cantor. In: Annals of Science, 1971, v. 27, No. 4, |
| 4. | Joseph Warren Dauben. Georg Cantor: his mathematics and philosophy of the infinite. Harvard University Press, 1979. |
| 5. | Ф. А. Медведев. Развитие теории множеств в XIX веке. М., Наука, 1965. |
| 6. | Н. Я. Виленкин. Рассказы о множествах. М., Наука, 1965. |
|
Джозеф У. Даубен (Joseph W. Dauben) — профессор истории и истории естествознания в колледже Герберта Г. Лемана при |