В МИРЕ НАУКИ Scientific American · Издание на русском языке № 1 · ЯНВАРЬ 1983 · С. 84–93

Короткая жизнь Эвариста Галуа



Согласно легенде, молодой математик создал теорию групп за одну ночь — накануне дуэли, на которой он был смертельно ранен. Более тщательные исследования показывают, что разработка этих замечательных идей заняла у Галуа несколько больше времени

ТОНИ РОТМАН

В предрассветные часы 30 мая 1832 года необыкновенно одарённый двадцатилетний математик Эварист Галуа писал своим друзьям Лебону и Делонэ:

«Меня вызвали на дуэль два патриота... Я не мог отказаться. Простите, что я не дал знать никому из вас. Противники взяли с меня честное слово, что я не предупрежу никого из патриотов.

Ваша задача очень проста: вам надо подтвердить, что я дрался против воли, т.е. после того, как были исчерпаны все средства мирно уладить дело, и что я не способен лгать даже в таком пустяке, как тот, о котором шла речь.

Не забывайте меня! Ведь судьба не дала мне прожить столько, чтобы мое имя узнала родина.

Умираю Вашим другом.

Э. Галуа».

В ту же ночь Галуа написал своему другу Огюсту Шевалье:

«Я открыл в анализе кое-что новое. Некоторые из этих открытий касаются теории уравнений, другие — функций, определяемых интегралами.

В теории уравнений я исследовал, в каких случаях уравнения разрешаются в радикалах, что дало мне повод углубить эту теорию и описать все возможные преобразования уравнения, допустимые даже тогда, когда оно не решается в радикалах.

Из этого можно сделать три мемуара...

Обратись публично к Якоби и Гауссу и попроси их высказать своё мнение, но не о верности теорем, а об их значении.

Я надеюсь, что после этого найдутся люди, которые сочтут для себя полезным навести порядок во всей этой неразберихе».

В свете последующих событий становится понятным состояние отчаяния, в котором Галуа писал эти письма. Ранним утром, закончив писать, он покинул свою комнату в парижской частной лечебнице Фолтрие и направился к находившемуся поблизости пруду, где ему предстояла дуэль с неким политическим активистом Пеше д'Эрбенвилем. Галуа ранили в живот и бросили на месте дуэли. Его нашёл прохожий и перевёз в больницу Кошэн, где он умер на следующий день. Четырнадцать лет спустя рукописи, которые Галуа оставил для Шевалье, опубликовал французский математик Жозеф Лиувилль. Эти статьи положили начало необыкновенно плодотворной ветви математики, названной теорией групп.

Немного найдётся в истории науки легенд, которые по своей романтичности могли бы сравниться с тем, что рассказывается о жизни и смерти Галуа. История его жизни так впечатляет, что очень легко прочесть слишком много между строк его писем. Хотелось бы наконец разобраться в событиях, приведших Галуа к дуэли, чтобы пролить свет на драму, отразившуюся в письмах.

Известно, например, что в семнадцать лет Галуа многое сделал для создания раздела математики, который ныне даёт возможность проникнуть в сущность таких различных областей, как теория чисел, кристаллография, физика элементарных частиц и возможные позиции кубика Рубика. Известно и то, что в том же возрасте Галуа вторично провалился на экзамене по математике при поступлении в Эколь Политекник (Политехнический институт). Ему пришлось поступить в Эколь Нормаль (Высшую педагогическую школу), но в девятнадцать лет он был оттуда исключён, дважды арестован и заключён в тюрьму за политическую деятельность. Незадолго до дуэли он пережил разочарование в любви; в одном из своих последних писем он, по-видимому, связывает это с дуэлью. «Я умираю, — писал он, — жертвой подлой кокетки».

Галуа в 17 лет, студент лицея Луи-ле-Гран. (Рисунок Д. Джонсона.) Начав изучать математику, Галуа уже через два года опубликовал статью о непрерывных дробях и приступил к исследованию теории уравнений, что привело его к абстрактной алгебраической теории множеств объектов, которые он назвал группами. Теорию групп развивали также многие другие математики конца XVIII – начала XIX века, а именно Паоло Руффини, Нильс-Хенрик Абель и Жозеф Луи Лагранж. Честь основания теории групп, однако, обычно приписывается Галуа. Рисунок выполнен по двум известным портретам Галуа. Один был сделан, когда Галуа было 15 лет, а другой закончен по памяти братом Галуа Альфредом в 1848 году, через 16 лет после смерти Эвариста.

К сожалению, в XX веке некоторые биографы Галуа не устояли перед искушением по-своему сопоставить, интерпретировать и приукрасить подобные факты. История жизни Галуа известна в основном по популярным его биографиям, таким, как книга физика Леопольда Инфельда и астронома Фреда Хойла. Наиболее распространённая версия этой истории принадлежит математику Эрику Темплу Беллу, чья книга «Творцы математики», вышедшая в 1937 году, пожалуй, самое известное описание жизни великих математиков.

В популярном изложении Галуа предстаёт как непонятый гений, угнетённый глупостью учителей, неизвестный в математических кругах своего времени и побуждаемый происходящими вокруг него событиями к политической деятельности, на которую уходила его энергия и которая в конечном счёте привела его к гибели. Согласно таким жизнеописаниям, самым примечательным было то, что в смутное время политических беспорядков и даже в тюрьме Галуа продолжал обдумывать свои математические идеи и наконец в ночь перед дуэлью записал их. Стоит привести здесь описание этой последней ночи, данное Беллом, поскольку именно оно, по-видимому, более всего способствовало распространению мифа о Галуа:

«Всю ночь напролёт он лихорадочно делал наброски своего научного завещания, тщательно собирая по частицам сокровища своего ума; писал, стараясь всё успеть перед смертью, неотвратимость которой была ему очевидна. Снова и снова он принимался царапать на полях: «У меня нет времени, у меня нет времени», — и переходил к следующей мысли. То, что он записал в эти последние полные отчаяния часы перед рассветом, даст пищу для размышления поколениям математиков на сотни лет».

Заметки на полях одной из статей, оставленных Галуа перед смертью. Это наиболее известный документ, который цитируется в подтверждение той версии, что Галуа записал свои мысли о теории групп в ночь перед дуэлью. С левой стороны листа написано: «Доказательство нуждается в некотором дополнении. У меня нет времени (примечание автора)». [«Il y a quelque chose à completer dans cette démonstration. Je n'ai pas le temps (Note d'A.).»] Согласно известному жизнеописанию Галуа, принадлежащему перу Э. Белла, фраза «У меня нет времени» часто встречается в рукописях. В действительности воспроизведённая здесь страница — единственное место, где есть эта фраза. Торопливый почерк, каким она написана, резко контрастирует с аккуратными строчками основного текста; это даёт основание предполагать, что в ночь перед дуэлью Галуа не писал эту статью, а только редактировал её. В самом деле, статья уже была представлена в Академию наук; Симеон Дени Пуассон возвратил рукопись Галуа с предложением переработать её.

Недавно с помощью М. Энно и С. Де-Витт-Моретт (Техасский университет, Остин) я изучил некоторые рукописи Галуа, а также последние научные работы о его жизни, показывающие, что основные факты его биографии известны давно. Воссозданная же Беллом и другими картина жизни Галуа даёт нам скорее стереотип гения науки, апеллирующий к воображению массового читателя, чем представление о реальной личности Галуа. Подлинная история жизни Эвариста Галуа увлекательна сама по себе и вполне заслуживает того, чтобы её рассказать в 150-ю годовщину его смерти.

Помимо писем, официальных записей и других документов того времени основным источником сведений о жизни Галуа является биография, написанная в 1896 году Полем Дюпюи, историком и старшим надзирателем Эколь Нормаль, в которой Галуа учился за 66 лет до него. Согласно книге Дюпюи, Галуа родился 25 октября 1811 года в городе Бур-ла-Рен близ Парижа. Его отец Никола Габриэль Галуа был сторонником Наполеона и возглавлял либеральную партию своего городка; он был избран мэром Бур-ла-Рена в 1815 году во время наполеоновских Ста дней.

До 12 лет Эвариста воспитывала мать, Аделаида Мария Демант Галуа. Она передала сыну солидные познания в греческом и латинском языках и свой скептицизм по отношению к господствующей религии. Маловероятно, однако, чтобы юный Галуа мог познакомиться с математикой в объёме, большем чем обычные уроки арифметики; математическое образование в то время не считалось чем-то важным. Неизвестно, имел ли кто-нибудь ещё в семье Галуа способности к математике.

Официально обучение Галуа началось в 1823 году, когда он поступил в Королевский лицей Людовика Великого (лицей Луи-ле-Гран), парижскую приготовительную школу, в которой в своё время учились Робеспьер и Виктор Гюго (эта школа существует и по сей день). В лицее сформировались политические взгляды Галуа. Либеральные, антироялистские симпатии, переданные ему родителями, совпадали с политическими взглядами большинства лицеистов.

В первый год пребывания Галуа в лицее отношения между лицеистами и вновь назначенным директором школы были весьма натянутыми. Лицеисты подозревали директора в намерении отдать школу иезуитам (иезуиты возглавляли правое крыло реакции, которая пришла на смену наполеоновской эпохе). Ученики доступными им средствами выражали свой протест: отказывались петь в церкви, отвечать в классе, провозглашать тост за здоровье Людовика XVIII на школьных банкетах. Директор исключил сразу 40 учеников как зачинщиков. Хотя Галуа и не исключили (и неизвестно, принимал ли он участие во всём этом), произвол директора, несомненно, усилил недоверие Галуа к властям.

Почти нет свидетельств того, что Галуа был плохим учеником или что низкий уровень преподавания в лицее сдерживал его интеллектуальное развитие, как следует из некоторых популярных книг. В первые годы обучения он завоевал несколько наград по греческому и латыни и получил полдюжины хвалебных отзывов. Историк науки Р. Татон называет его успехи блестящими. Правда, на третьем курсе лицея Галуа недостаточно хорошо занимался по классу риторики, и его оставили на второй год. Белл утверждает, что Галуа пренебрегал риторикой из-за чрезмерных занятий алгеброй, однако он записался в класс математики уже после того, как был оставлен на второй год. Галуа было тогда 15 лет. Занятия в этом классе, которые вёл Ипполит Жан Вернье, пробудили в Галуа его математический гений. Без труда освоив учебную программу, он сразу взялся за работы выдающихся учёных того времени, с увлечением изучил книгу геометра Лежандра и труды Лагранжа: «Решение алгебраических уравнений», «Теория аналитических функций» и «Лекции по дифференциальному исчислению». Несомненно, именно у Лагранжа Галуа впервые встретился с теорией уравнений, в которую в течение последующих четырёх лет он сделал фундаментальный вклад. По-видимому, Вернье по достоинству оценил талант своего ученика: в отзыве на отчёт Галуа за триместр он пишет о «старании и успехе», «старании и очень заметном прогрессе» и т.п.

Открыв для себя мир математики, Галуа сильно переменился. Он стал небрежно относиться к занятиям по другим предметам, чем вызвал враждебное к себе отношение учителей по гуманитарным наукам. Преподаватели риторики называют его рассеянным, в отчёте за триместр и в отзывах появляются слова «замкнутый», «странный», «своеобразный». Даже Вернье, который не стремился охладить страсть Галуа к математике, советовал ему заниматься более систематически. Галуа не последовал его совету: он решил держать вступительный экзамен в Политехнический институт на год раньше и без обычного подготовительного курса по математике. И провалился, так как недостаточно глубоко знал основы математики.

Галуа считал, что с ним обошлись несправедливо, провал ещё более настроил его против властей. Тем не менее быстрые успехи в математике продолжаются, и Галуа записывается в лицее в математический класс более высокого уровня, который вёл очень опытный преподаватель Луи Поль Эмиль Ришар. Ришар сразу понял, как одарён Галуа, и обратился с просьбой о его приёме в Политехнический институт без экзаменов. Хотя эта просьба не возымела последствий, одобрение Ришара оказало на юношу чудесное влияние. В марте 1829 года, когда Галуа был ещё студентом, вышла его первая статья. Она называлась «Доказательство одной теоремы о периодических непрерывных дробях» и появилась в журнале Annales de mathématiques pures et appliquées, который издавал Жозеф Диаз Жергон.

Однако тема статьи была в стороне от главных научных интересов Галуа. В то время он уже обратился к теории алгебраических уравнений, которую начал изучать по трудам Лагранжа. В возрасте 17 лет Галуа взялся за одну из самых трудных в математике проблем, которая сто с лишним лет заводила учёных в тупик.

В 1829 году центральной проблемой теории уравнений был вопрос, при каких условиях алгебраическое уравнение можно разрешить. Точнее, каким должен быть метод решения уравнения с одним неизвестным x, все коэффициенты которого являются рациональными числами, причём член наивысшей степени равен xⁿ? Метод должен быть общим и применяться ко всем подобным уравнениям и должен включать лишь четыре элементарные операции (сложение, вычитание, умножение и деление) и операцию извлечения корня. Если решения (корни) уравнения можно получить из коэффициентов уравнения только при помощи этих операций, то говорят, что уравнение разрешимо в радикалах.

Накопленный опыт как будто подсказывал, что решение уравнения n-й степени не потребует более сложных операций, чем извлечение корня n-й степени. Решение квадратного уравнения общего вида или уравнения второй степени ax² + bx + c = 0, известное ещё вавилонянам, требует извлечения квадратного корня из некоторой комбинации коэффициентов, а именно из выражения b² – 4ac. Таким образом, общее квадратное уравнение разрешимо в радикалах. Точно так же общее решение кубического уравнения, которое нашли в начале XVI века итальянские математики Сципион дель Ферро и Никколо Фонтана (Тарталья), сводится к извлечению кубического корня из некоторой комбинации коэффициентов. Решение уравнения четвёртой степени общего вида, впервые полученное итальянским математиком Лудовико Феррари примерно в то же время, требует извлечения корней четвёртой степени.

До Галуа почти триста лет никому не удавалось решить в радикалах общее уравнение пятой степени или выше. Многие математики склонялись к мысли, что общее решение такого вида невозможно, хотя в частных случаях, например в случае уравнения x⁷ – 2 = 0, решение можно найти в радикалах. (В этом примере одно из решений — это ⁷√2.) Галуа нашёл окончательные критерии, которые позволили определить, существует ли решение данного уравнения в радикалах. Пожалуй, методы, которые Галуа разработал для решения этой проблемы, ещё более замечательны, чем собственно открытия в теории уравнений. Его исследования привели к теории, называемой ныне теорией групп, приложения которой далеко выходят за рамки теории уравнений.

Свою первую статью в той области, которая в дальнейшем превратится в теорию групп, Галуа представил во Французскую академию наук 25 мая 1829 года, незадолго до окончания лицея. Менее чем через два месяца ему снова предстояло держать вступительный экзамен в Политехнический институт, однако события приняли несчастливый оборот. Второго июля, т.е. за несколько недель до экзамена, отец Эвариста покончил жизнь самоубийством, не вынеся скандала вокруг своего имени. (Приходский священник-иезуит Бур-ла-Рена оклеветал старшего Галуа, распространив среди родственников и знакомых Галуа злые эпиграммы на него.) Обстановка для экзамена сложилась крайне неблагоприятная. Кроме того, на экзамене Эварист, по-видимому, отказался следовать предложенной экзаменатором схеме ответа; в результате Галуа провалился опять, на этот раз окончательно. Несчастья обострили его ненависть к правившей тогда во Франции консервативной администрации.

Вынужденный подумать теперь о менее престижной Эколь Нормаль (называвшейся тогда Эколь Препаратуар), Галуа в ноябре 1829 года выдержал необходимый для поступления экзамен. На этот раз его приняли благодаря очень высокому баллу по математике, и примерно в то же время, когда его статья по теории групп была представлена в Академию наук, он стал студентом. Однако статья Галуа не была зачитана на заседании Академии.

Дело в том, что рецензентом назначили Огюстена Луи Коши — самого известного в ту пору французского математика, который был верным сторонником консервативной реставрации. Коши уже занимался комбинаторикой, предшественницей теории групп; позднее он написал много работ, посвящённых теории групп. Распространена версия, что Коши потерял, забыл или выбросил рукопись Галуа; но больше похоже на правду, что Коши, понимая её значение, обращался с ней бережно. Действительно, из письма, обнаруженного Татоном в 1971 году в архивах Академии, явствует, что 18 января 1830 года Коши намеревался выступить на заседании Академии с изложением результатов Галуа. Коши писал: «Сегодня я должен был представить Академии отчёт о работах Галуа... Я болен и остался дома. Сожалею, что не имею возможности присутствовать на сегодняшнем заседании, и хотел бы, чтобы вы включили в расписание следующего заседания моё выступление по вышеуказанному предмету».

Однако на следующей неделе, когда Коши выступал перед Академией со своим собственным докладом, он не представил работу Галуа. Почему так получилось — остаётся предметом догадок. По мнению Татона, Коши настаивал на том, чтобы Галуа расширил свою статью и представил её на соискание высшей награды Академии по метематике. Хотя предположение Татона не подтверждается документами, Галуа действительно представил свою работу на конкурс в феврале, за месяц до истечения срока конкурса. Статья была послана постоянному секретарю Академии Жану Батисту Фурье, математику, разработавшему метод анализа, который ныне называют анализом Фурье. Однако в мае Фурье умер, и рукопись Галуа среди его бумаг не нашли. Впоследствии Галуа приписывал своё невезение козням со стороны Академии, обвиняя конкурсную комиссию в произволе, — его работу отклонили только потому, что его фамилия Галуа и он всего лишь студент. Некоторые склонны серьёзно относиться к утверждению Галуа, однако надо учитывать, что его позиция по отношению к властям была несколько аффектированной.

Несмотря на неудачи, Галуа продолжал плодотворно работать и начал публиковать свои труды в Bulletin des sciences mathématiques, astronomiques, physiques et chimiques, издававшемся бароном Феруссаком, — менее видном издании, чем публикации Академии наук. Из его статей ясно, что в 1830 году он ушёл далеко вперёд в исследовании условий, определяющих разрешимость уравнений, хотя ещё и не получил полного решения этой проблемы. В январе 1831 года он завершил работу и, следуя настоятельным советам математика Симеона Дени Пуассона, представил её в Академию наук. Эта статья — самая значительная работа Галуа, и тот факт, что она вышла в свет более чем за год до дуэли, лишает смысла историю о том, что все свои работы по теории групп Галуа написал за одну ночь.

Чтобы понять работу Галуа, бесполезно изучать его оригинальные статьи. Пуассон, несомненно, старался разобраться в рукописи 1831 года, но в конце концов рекомендовал Академии наук отклонить её, посоветовав при этом Галуа расширить статью и сделать изложение более ясным. Пуассон также отверг одно из доказательств Галуа, посчитав его неверным, хотя справедливость утверждения Галуа могла быть доказана при помощи одного результата, полученного Лагранжем. Согласно П. Нюмену из Оксфордского университета, критические замечания Пуассона были справедливы. Аргументация Галуа очень кратка и сжата, что чрезвычайно затрудняет её понимание; кроме того, встречаются и неточности. Сейчас, через сто пятьдесят лет, можно сформулировать основы теории в доступной форме. Для этой цели я обратился за помощью к астрофизику А. Отвиллу из Оксфорда.

Что такое группа? По сути теория групп связана с симметриями, присущими какой-либо системе. Представьте себе снежинку, вершины которой отстоят друг от друга на 60°. Если снежинку повернуть вокруг оси, проходящей через её центр перпендикулярно к её плоскости, на 60° или на число градусов, кратное 60, то её вид в целом останется неизменным, даже если какая-нибудь вершина и изменила своё положение. Операция, которая оставляет общий вид фигуры неизменным в этом смысле, называется операцией симметрии.

Если снежинку последовательно дважды повернуть на число градусов, кратное 60, то её вид останется неизменным, причём положение вершин будет одним из тех, которые можно достичь и одной операцией (поворотом). Например, поворот на 60° против часовой стрелки, за которым следует поворот на 240° по часовой стрелке, эквивалентен повороту на 180° по часовой стрелке. Вообще, если обозначить через R(n) поворот на 60n градусов и если результат двух таких операций записать в виде R(n)*R(m), тогда для всех целых n и m операция R(n)*R(m) эквивалентна R(n+m). Эта эквивалентность означает, что «произведение» двух операций симметрии есть также операция симметрии.

Есть ещё три важных свойства поворачивания снежинки. Во-первых, поворот на 0°, или R(0), всегда оставляет её вид неизменным, поскольку ничего не меняется. Сочетание («произведение») любого поворота R(n) и поворота R(0) равно R(n), так что R(0) играет ту же роль в поворотах снежинки, что и число 1 в обыкновенном умножении. Поэтому R(0) называют единичным поворотом. Во-вторых, если произвести сначала поворот R(n), а вслед за ним поворот в противоположном направлении на ту же величину, который можно обозначить R(–n), снежинка вернётся в исходное положение. Таким образом, произведение R(n)*R(–n) эквивалентно R(0). Поворот R(–n) называется обратным к повороту R(n). В-третьих, операция R(m)*R(n)*R(p) всегда однозначна, так как [R(m)*R(n)]*R(p) эквивалентно действию R(m)*[R(n)*R(p)]. Это формальное свойство операции *, посредством которой комбинируются два поворота; оно называется ассоциативностью.

Четыре свойства, справедливые для комбинаций поворота снежинки, присущи любому множеству операций симметрии над любой системой; они называются групповыми свойствами. Система не обязательно должна быть геометрической фигурой, как снежинка. Например, уравнение также является системой, свойства симметрии которой можно описать групповыми аксиомами. Обобщив, мы можем сказать, что группа состоит из элементов, или операций a, b, c и т.д., и правила, обозначенного *, посредством которых осуществима комбинация двух элементов. Предполагается, что группа замкнута относительно операции *, а именно комбинация a*b для любых элементов a и b группы также является элементом группы. Группа должна включать единичный элемент 1, который определяется следующим образом: для любого элемента a группы комбинация a*1 равна a. Далее, для каждого элемента a должен существовать обратный элемент a^–1, такой, что a*a^–1 = 1. Наконец, предполагаемся, что элементы группы и групповая операция удовлетворяют свойству ассоциативности, которое утверждает, что (a*b)*c равно a*(b*c).

Теория групп является одной из самых плодотворных областей математики. Белл был прав, когда писал, что она на сотни лет дала математикам пищу для исследования. Одним из самых важных недавних достижений теории групп был результат, который в январе 1981 года представил на заседании Американского математического общества Даниэл Горенстейн из Университета Ратгерс. Горенстейн доказал, что список из 26 групп, носящих название спорадических конечных простых групп, является полным. Из этого открытия в некотором смысле вытекает, что компоненты, или «строительные блоки», любой группы с конечным числом элементов теперь исчерпывающим образом классифицированы.

Другой совокупностью нечисловых элементов, удовлетворяющих групповым аксиомам, является группа перестановок фиксированного числа объектов. Переставляемыми объектами могут быть, например, шахматные фигуры или буквы алфавита. Существенно, однако, что элементами группы являются не шахматные фигуры, не буквы, а действия, в результате которых получаются различные перестановки объектов. Чтобы найти «произведение» двух элементов a и b группы (т.е. найти a*b), надо найти результат первой перестановки совокупности объектов и применить вторую перестановку к этому результату.

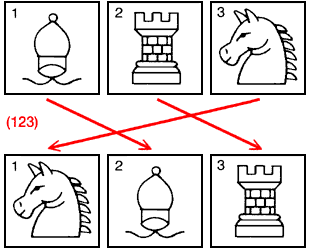
Предположим, что три шахматные фигуры расположены так, что ладья занимает клетку № 1, конь занимает клетку № 2, а слон — клетку № 3. Один элемент группы перестановок для этих объектов можно записать как (12); это действие перемещает объект из клетки 1 в клетку 2, а объект из клетки 2 в клетку 1. В результате действия элемента (12) на расположение ладья–конь–слон ладья и конь меняются местами и получается расположение конь–ладья–слон. Если снова проделать эту операцию, то объекты в тех же клетках снова поменяются местами и снова получится расположение ладья–конь–слон.Таким образом, элемент (12) является обратным самому себе.

Другой элемент группы, обозначенный (123), переставляет объект из клетки 1 в клетку 2, объект из клетки 2 в клетку 3 и объект из клетки 3 в клетку 1. Предположим, что первоначальное расположение объектов ладья–конь–слон преобразовано с помощью элемента (12) в расположение конь–ладья–слон. Теперь применяется элемент (123), создавая расположение слон–конь–ладья. Это расположение можно достичь за один шаг, применив к первоначальному, исходному, расположению перестановку (13), которая меняет местами объекты из клеток 1 и 3. Таким образом, результат перестановки (12), к которому применили перестановку (123), создает то же самое расположение объектов, что и перестановка (13). В символической записи: (12)*(123) = (13).

Идея группы видна на примере группы S(3), которая является группой перестановок трёх объектов. Элемент группы S(3) действует над объектами, переставляя их. Перестановка (123) передвигает объект из клетки 1 в клетку 2, объект из клетки 2 в клетку 3 и объект из клетки 3 в клетку 1. Так как три объекта могут располагаться шестью способами, группа S(3) состоит из шести элементов.

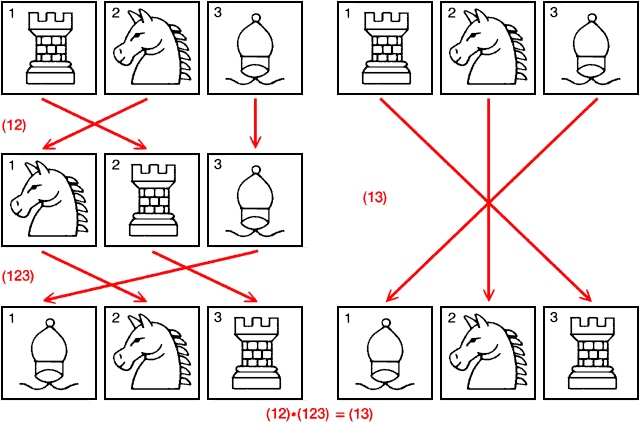«Умножение» одного элемента группы S(3) на другой. Чтобы «умножить», надо определить то расположение объектов, которое получится в результате первой перестановки, а затем применить к этому расположению вторую перестановку. Произведением двух перестановок называется единственная перестановка, которая даёт то же расположение объектов. Обычно умножение групп не коммутативно: произведение двух элементов зависит от порядка, в котором они берутся. Так, (12)*(123) = (13), (123)*(12) = (23).

2-й элемент 1-й элемент (1)   (123)   (132) (12) (13) (23) (1) (1) (123) (132) (12) (13) (23) (123) (123) (132) (1) (23) (12) (13) (132) (132) (1) (123) (13) (23) (12) (12) (12) (13) (23) (1) (123) (132) (13) (13) (23) (12) (132) (1) (123) (23) (23) (12) (13) (123) (132) (1)

Таблица умножения для шести перестановок трёх объектов подтверждает, что перестановки удовлетворяют аксиомам группы. Таблица показывает, что для каждой пары перестановок a и b их произведение a*b само является перестановкой. Имеется единичный элемент, а именно элемент (1), обладающий тем свойством, что a*(1) равно a. Для каждого элемента a существует элемент, называемый обратным, или a–1, со следующим свойством: a*a–1, равно (1). Например, обратный элемент к (123) есть (132). Наконец, закон ассоциативности, утверждающий, что для любых перестановок a, b и c произведение a*(b*c) равно (a*b)*c, можно проверить с помощью этой таблицы. Красным выделено подмножество из шести перестановок. Их таблица умножения (тоже выделена красным) показывает, что они образуют группу. Такая группа, содержащаяся в другой группе, называется собственной подгруппой.

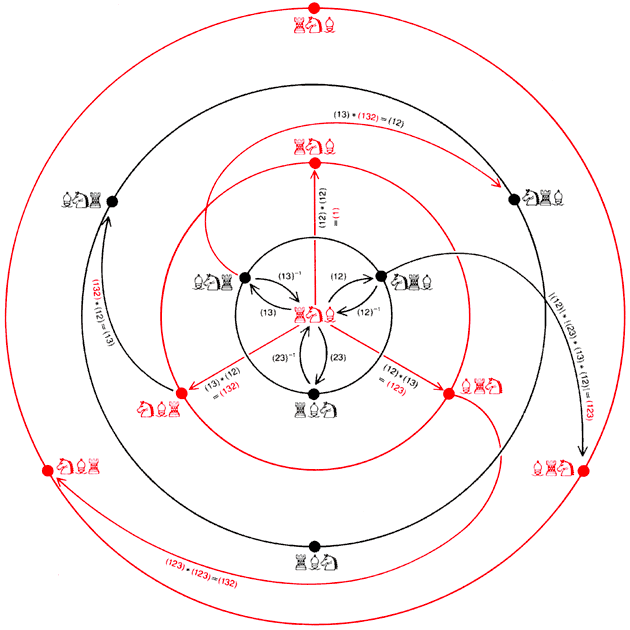Перестановки в группе S(3) могут быть неизменно записаны как произведение перестановок, которые меняют местами лишь два объекта. Если перестановку можно записать как произведение чётного числа таких перестановок, она называется чётной; в противном случае она нечётная. Если чётная перестановка (цветные круги) умножается на чётную (цветные стрелки), произведение будет тоже чётной перестановкой. Если чётная перестановка умножается на нечётную (чёрные стрелки), произведение нечётно. Аналогично, если нечётная перестановка (чёрные круги) умножается на чётную, произведение нечётно, в то время как нечётная перестановка, умноженная на нечётную, даёт чётную перестановку. Чётные перестановки образуют подгруппу, а именно подгруппу, выделенную красным на предыдущем рисунке. Эта подгруппа называется знакопеременной, или A(3). Такая подгруппа, как A(3), называется нормальной подгруппой группы S(3), если для любого элемента h из A(3) и любого элемента g из S(3) элемент g*h*g–1 также является элементом A(3). Для того чтобы доказать, что A(3) — нормальная подгруппа группы S(3), предположим, что g — чётная перестановка. Тогда g*h*g–1 есть произведение трёх чётных перестановок, которое также является чётной перестановкой, и, таким образом, является элементом группы A(3). Если g — нечётная перестановка, g*h*g–1 — произведение нечётной перестановки на чётную и ещё на нечётную, которое является чётной перестановкой. Следовательно, A(3) — нормальная подгруппа. Подобным же образом можно показать, что для любого числа n подгруппа A(n) является нормальной подгруппой группы S(n). Число элементов подгруппы должно быть делителем числа элементов основной группы. Так как в A(n) вдвое меньше элементов, чем в S(n), A(n) содержит максимальное число элементов, которое может иметь собственная подгруппа группы S(n). Значит, A(n) — максимальная нормальная подгруппа.

Число перестановок, или размещений, n объектов равно n!. Факториал числа n есть произведение всех чисел от 1 до n включительно; например, 5! равно 1×2×3×4×5, или 120. Следовательно, число элементов в группе S(n), группе перестановок n объектов, равно n!. Число элементов в группе называется её «порядком». Группа перестановок трёх объектов S(3) содержит 3!, или 6 элементов: (1), (12), (13), (23), (123), (132). Здесь (1) — единичная перестановка, которая оставляет любое расположение объектов неизменным.

Оказывается, что некоторое подмножество множества элементов группы S(3) само может удовлетворять всем свойствам группы; в этом случае говорят, что оно образует подгруппу. Если число элементов подгруппы меньше числа элементов самой группы, подгруппа называется собственной. Например, легко проверить, что [(1), (12)] является группой и, значит, собственной подгруппой группы S(3).

Для любой собственной подгруппы H группы G можно определить число, называемое индексом: это порядок основной группы, делённый на порядок подгруппы; обычно он записывается как [G/H]. Индекс подгруппы [(1), (12)] в группе S(3) равен 6/2, т.е. 3. Согласно элементарной теореме теории групп, которую мы не будем здесь доказывать, порядок любой подгруппы должен быть делителем порядка основной группы, так что индекс всегда целое число.

Галуа ввёл три важнейших понятия, взаимосвязь которых позволила ему доказать, что нет общего метода решения уравнений пятой степени или выше в радикалах. (Точнее, эта взаимосвязь позволила ему построить теорию разрешимости уравнений в радикалах. Неразрешимость в радикалах уравнений пятой степени была доказана ранее норвежским математиком Н.-Х. Абелем. — Ред.) Прежде всего Галуа отметил, что каждое уравнение можно связать с некоторой группой перестановок. Такая группа отражает свойства симметрии уравнения; теперь она именуется группой Галуа.

Чтобы понять роль свойств группы Галуа, рассмотрим произвольное уравнение третьей степени с рациональными коэффициентами. Можно доказать, что такое уравнение имеет три корня, однако доказательство не говорит нам, возможно ли эти корни выразить в виде радикалов. Если обозначить корни уравнения через u, v и w, то из них можно составить полиномиальную функцию, например u–v или uv+w–1. Любую такую функцию можно превратить в другую функцию перестановкой корней u, v и w. Например, перестановка (12) меняет местами u и v и таким образом превращает функцию u–v в функцию v–u. В результате такой перестановки многие функции корней изменяют своё значение, но некоторые не изменяются. Например, функция u+v+w не изменяет значения при любой перестановке u, v и w. Поскольку группа S(3) содержит все возможные перестановки u, v и w, говорят, что u+v+w инвариантна по отношению к S(3).

Можно показать, что значение u+v+w — рациональное число для любого уравнения третьей степени с рациональными коэффициентами. Другие полиномиальные функции корней могут быть рациональными для некоторых уравнений и иррациональными для других, в зависимости от коэффициентов уравнения. Если значение такой функции рационально, то существует некоторая группа перестановок u, v и w, которая не изменяет значения функции. Группа Галуа уравнения является наибольшей группой перестановок, которая удовлетворяет этому требованию для любой рациональнозначной полиномиальной функции корней. Другими словами, для любой полиномиальной функции корней, имеющей рациональные значения, любая перестановка из группы Галуа оставляет значение функции неизменным. Когда перестановка корней не меняет значение некоторой рациональнозначной полиномиальной функции этих корней, то корни неразличимы относительно этой перестановки. Следовательно, чем больше число элементов группы Галуа, тем больше она содержит перестановок, для которых корни неразличимы. По этой причине группа Галуа — мощное средство для представления свойств симметрии уравнения.

Вычислить группу Галуа для данного уравнения обычно очень сложно, хотя в принципе это всегда можно сделать, даже не зная значений корней уравнения. Для целей Галуа, однако, вычисление было необязательно. Ему нужно было показать только, что всегда найдутся уравнения порядка n, чья группа Галуа — наибольшая возможная группа перестановок корней, а именно S(n).

Галуа ввёл также понятие нормальной подгруппы. Подгруппа H группы G нормальна в G тогда и только тогда, когда выполняется следующее условие: если «умножают» любой элемент h подгруппы H слева на любой элемент g основной группы G, а затем «умножают» произведение справа на g^–1 (обратный элемент к g), получается элемент подгруппы H. Можно записать, что если H нормальна в G, то существует элемент h' в H, такой, что h' = g*h*g^–1. Например, можно легко убедиться, что [(1),(123),(132)] является нормальной подгруппой группы S(3) (см. таблицу).

Если конечная группа G имеет несколько нормальных подгрупп, должна найтись одна подгруппа, порядок которой больше порядков всех нормальных подгрупп группы G; она называется максимальной нормальной подгруппой группы G. Аналогично, максимальная нормальная подгруппа сама может иметь максимальную нормальную подгруппу, и этот процесс продолжается, пока не будет достигнута наименьшая возможная нормальная подгруппа. Следовательно, любая группа G порождает последовательность максимальных нормальных подгрупп. Если такую последовательность обозначить G, H, I, J, ..., то можно определить ряд индексов максимальных нормальных подгрупп [G/H], [H/I], [I/J], и т.д.

Третье важное понятие теории Галуа — понятие разрешимой группы. Галуа называл группу разрешимой, если каждый из индексов максимальных нормальных подгрупп, порожденных группой, есть простое число. Например, максимальная нормальная подгруппа группы S(3) есть [(1),(123),(132)]. В свою очередь максимальная нормальная подгруппа группы [(1),(123),(132)] есть [(1)]. Индекс подгруппы [(1),(123),(132)] в группе S(3) есть 6/3, или 2, а индекс подгруппы [(1)] в группе [(1),(123),(132)] есть 3/1, или 3. Поскольку и 2, и 3 — простые числа, S(3) — разрешимая группа.

Термин разрешимая группа хорошо оправдывался теорией Галуа: Галуа показал, что уравнение разрешимо в радикалах тогда и только тогда, когда группа Галуа этого уравнения — разрешимая группа. Чтобы доказать, что уравнения пятой степени и выше нельзя в общем случае решить в радикалах, нужно было показать, что существуют уравнения такого рода, для которых группа Галуа неразрешима. Группа S(n) — неразрешимая группа, когда n больше или равно 5. Так как для всех таких значений n существуют уравнения степени n, для которых S(n) является группой Галуа, общее уравнение пятой степени или выше неразрешимо.

Когда Галуа заканчивал работу над теорией групп, в его жизнь ворвались политические события. В июле 1830 года республиканцы — противники восстановленной монархии вышли на улицы; Карл X был вынужден эмигрировать. В то время как революционно настроенные студенты Политехнического института активно участвовали в этих событиях, Галуа и его товарищей по Эколь Препаратуар заперли внутри школы по приказу директора. Возмущённый Галуа пытался сбежать, но ему это не удалось, так что он остался в стороне от событий июльской революции.

Отречение Карла X казалось большой победой республиканцев, однако на троне оказался Луи-Филипп, к великому разочарованию Галуа и других либералов. В последовавшие за революцией месяцы Галуа посещал собрания республиканцев, встречался с их лидерами (особенно с Франсуа Венсаном Распаем) и, по-видимому, принимал участие в волнениях и демонстрациях, лихорадивших Париж. Он вступил в артиллерию Национальной гвардии — подразделение милиции, состоявшее почти исключительно из республиканцев. В декабре Галуа написал в одну из парижских газет письмо, в котором называл директора Эколь Препаратуар предателем, имея в виду его поведение во время июльской революции; неудивительно, что после этого Галуа исключили.

В противоположность традиционной легенде, Галуа вовсе не производит впечатления жертвы обстоятельств. Напротив, он, похоже, был сорвиголовой и постоянно попадал в переделки. Из письма математика Софи Жермен следует, что Галуа регулярно присутствовал на заседаниях Академии наук и обычно всячески нападал на выступающих. Когда Галуа исключили из Эколь Препаратуар, он переехал в парижский дом своей матери, но ей оказалось трудно с ним ужиться, и она уехала.

Для Галуа кульминация бурной весны 1831 года наступила 9 мая во время банкета республиканцев, которые праздновали оправдание девятнадцати артиллерийских офицеров, обвинённых в заговоре против правительства. В своих мемуарах Александр Дюма-отец, который присутствовал на этом банкете, пишет, что Галуа встал и предложил тост за Луи-Филиппа, при этом одновременно с бокалом он поднял кинжал. На следующий день Галуа арестовали, и он провёл больше месяца в тюрьме св. Пелагеи.

На суде защитник Галуа утверждал, что тост на самом деле звучал так: «За Луи-Филиппа, если он предаст», однако конец фразы потонул в шуме. Либо судьи поверили защите, либо их тронула молодость Галуа, но они его оправдали. Тем не менее в день взятия Бастилии, 14 июля 1831 года — т.е. не прошло и месяца после суда, — Галуа снова арестовали, на этот раз за незаконное ношение формы артиллерийской гвардии. Гвардия была распущена как угроза короне, поэтому поступок Галуа был вызывающим. На этот раз он провёл в тюрьме св. Пелагеи восемь месяцев.

Тюремное заключение сломило Галуа: он впадал то в ярость, то в уныние. Распай, который находился в тюрьме в это же время, позже вспоминал, что однажды Галуа в состоянии опьянения пытался покончить с собой. Согласно Распаю, Галуа говорил, что его преследует видение собственной кончины: «Я умру на дуэли по вине какой-нибудь кокетки низкого пошиба. Почему? Потому что она заставит меня защищать её честь, которую оскорбит другой». Когда погиб один из заключённых, Галуа, по-видимому, обвинил тюремного надзирателя в том, что тот подстроил убийство. За это Галуа посадили в карцер.

Самой большой неприятностью было то, что статьи, написанные Галуа в течение 1831 года, не напечатали. В исполненном горечи предисловии к тюремным запискам он утверждал: «Мне некого благодарить ни за совет, ни за поддержку. Благодарность была бы ложью».

Последний период жизни Галуа всегда особенно привлекал его биографов. Они не желали верить самому Галуа, что причиной дуэли была личная ссора, а вместо этого выискивали каких-то продажных женщин, полицейских провокаторов и политических противников и обвиняли их в гибели Галуа. Однако ни одна из подобных версий не подтверждается.

В середине марта 1832 года из-за свирепствовавшей тогда в Париже эпидемии холеры Галуа перевели из тюрьмы св. Пелагеи в частную лечебницу Фолтрие. По-видимому, именно здесь он и встретил ту «подлую кокетку». Роман был коротким, однако нелепо утверждать, что героиня его была продажной женщиной или платным агентом и намеренно подстроила убийство. Эпитет «подлая» связывали со словами «какая-нибудь кокетка низкого пошиба», и таким образом как бы подтверждалась версия о продажной женщине. Согласно свидетельству Распая, фразу о кокетке низкого пошиба Галуа произнёс за год до дуэли; вполне возможно, что это слова самого Распая. Кроме того, 25 мая, за шесть дней до смерти, в письме к Огюсту Шевалье Галуа намекает, что его роман оборвался: «Но как изгладить следы той бури страстей, через которую я прошёл? Как утешиться, когда за один месяц исчерпан до дна источник самого сладостного блаженства, отпущенного человеку, когда он выпит без радости и без надежды, когда знаешь, что он иссяк навсегда?» Кто же была эта женщина? Перед дуэлью Галуа получил два письма, в них упоминалась какая-то ссора, в которой он, видимо, был виновен более, чем сам это признавал. Первое письмо начинается так: «Пожалуйста, давайте порвём наши отношения. У меня нет сил продолжать с Вами переписку, но я попытаюсь обсудить с Вами всё, как я делала до того, как все это случилось...». Второе письмо написано в том же духе, и оба они подписаны «Стефания Д.». В рукописях Галуа К. Инфантоцци из Университета республики в Уругвае прочёл имя, которое Галуа стёр: Стефания Дюмотель. Инфантоцци установил, что это Стефания Фелисия Потерэн дю Мотель, дочь врача лечебницы Фолтрие. Позже она вышла замуж за преподавателя словесности.

Имя женщины, которую Галуа обвиняет в своих бедах в письме, написанном в ночь накануне дуэли, часто появляется на полях статей Галуа. На факсимиле под именем Эварист можно прочесть имя Стефания; Галуа также объединил буквы «С» и «Э» в монограмме. Из писем и других рукописей ясно, что злой эпитет «подлая кокетка» вышел из-под пера Галуа в связи с разочарованием в любви к женщине, которую он встретил всего за несколько месяцев до дуэли. Её личность установлена: это Стефания Фелисия Потерэн дю Мотель, дочь парижского врача.

Брат Галуа Альфред утверждал, что Эвариста убили преднамеренно, но маловероятно, чтобы убийцу подкупили антиреспубликанцы. Согласно Дюма, противником Галуа был Пеше д'Эрбенвиль, пылкий республиканец. В самом деле, д'Эрбенвиль — один из тех девятнадцати офицеров, чьё оправдание послужило поводом для вызывающего тоста Галуа. Кроме того, когда во время революции 1848 года разоблачали агентов короля, имя д'Эрбенвиля не упоминалось. В статье, недавно присланной мне Татоном, говорится, что дуэль происходила между друзьями и представляла собой что-то вроде «русской рулетки», когда заряжают только один пистолет.

В ночь перед дуэлью Галуа лишь отредактировал две рукописи и изложил их содержание и содержание ещё одной статьи в длинном письме к Шевалье. Одна из рукописей была той самой статьёй, которую отклонил Пуассон, другая — отрывок статьи, ранее опубликованной в Bulletin Феруссака. Третью рукопись не нашли, и её содержание известно лишь из краткого изложения в письме; по-видимому, она касается интегралов от общих алгебраических функций.

Как же быть со знаменитой фразой: «У меня нет времени», которую Галуа якобы вновь и вновь писал на полях, не успевая закончить работу? Эта фраза действительно есть на полях первой статьи, но встречается всего один раз. Рядом с ней в скобках написано: «Примечание автора».

Я не думаю, что представленные мною факты из жизни Эвариста Галуа сколько-нибудь умаляют его значение как математика. Сохранившиеся рукописи Галуа говорят о том, что, и попав в тюрьму, он продолжал вести математические изыскания и не оставлял их вплоть до самой смерти. То, что он мог продуктивно работать в таких условиях, свидетельствует о необыкновенной силе его воображения и интеллекта. Каковы бы ни были обстоятельства, в которых жил Галуа, нет сомнения, что ему принадлежит одна из самых оригинальных идей в математике.

Однако его репутация, так же, впрочем, как и история науки вообще, не вписывается в распространённое представление, согласно которому гений науки должен быть безупречен в частной жизни, а те его современники, которые не сумели понять его гениальности, непременно глупцы, убийцы, продажные женщины и т.п. Избитое утверждение «Посредственность не терпит гениальности» — несерьёзная основа для анализа исторических фактов, иначе пришлось бы судить о гении лишь по его экстравагантным выходкам, вроде тоста с кинжалом в руках.