Читателю, вероятно, известны на первый взгляд трудные геометрические задачи, которые мгновенно решаются, если заменить одну данную точку другой, симметричной ей относительно какой-то прямой. Соображения симметрии очень важны и в алгебре.

В этой статье мы рассмотрим ряд ситуаций, в которых число вида a + b√d полезно заменить сопряжённым a – b√d. Мы увидим, как этот простой приём — замена знака перед радикалом — помогает в решении разнообразных задач алгебры и анализа — от нехитрых оценок и преобразований до трудных олимпиадных задач и замысловатых придумок составителей конкурсных экзаменов.

Большинство наших примеров может служить первым знакомством с глубокими математическими теориями (кое-где мы указываем статьи и книги для продолжения знакомства). Среди задач, включённых в статью, две — из Задачника «Кванта» и несколько — из писем читателей, уже испытавших удовольствие от трюков с радикалами и желающих поделиться им с другими.

Пары сопряжённых чисел появляются вполне естественным образом, когда мы решаем квадратное уравнение, а корень из дискриминанта не извлекается: скажем, уравнение λ² – λ – 1 = 0 имеет пару «сопряжённых» корней:

К этому мы ещё вернёмся, а начнём с примеров другого рода: займёмся «перебросками»...

Если в книжке указан ответ к задаче (3 + √7)/2, а у вас получилось 1/(3 – √7) — не спешите искать ошибку в решении: ответ правильный — эти числа равны, потому что

Вот несколько характерных примеров, где полезно перенести «иррациональность» из числителя в знаменатель или наоборот.

 1.  Найти сумму

Эта сумма мгновенно «сворачивается», если переписать её так:

По выражению из статьи [1] «остаются крайние» (см. также [5]).

 2.  Доказать, что для любых натуральных m и n

где  α = √3 + √2.

Подобный факт мы использовали недавно при решении трудной задачи М514 ([2]).

В самом деле, всегда

поскольку число |m² – 2n²| — целое и отлично от 0 (равенство m² = 2n² невозможно — подумайте, почему!). Если бы выполнялось неравенство, противоположное (1), то должно было бы быть m < n√2 + 1/αn и

Но из (2) и (3) следует (1). Значит, наше предположение неверно, то есть (1) выполнено.

Неравенство (1) показывает, что число √2 сравнительно плохо приближается дробями с небольшими знаменателями; аналогичное неравенство (только с другим коэффициентом α) выполнено не только для √2, но и для любой «квадратичной иррациональности». Разумеется, (1) выполнено и при всех  α > √3 + √2, но константа  √3 + √2  здесь не наименьшая из возможных. Вопросы о приближениях квадратичных иррациональностсй рациональными числами — далеко продвинутая и важная для приложений область теории чисел ([3], [4]); с приближениями числа √2 мы ещё встретимся ниже (см. упражнение 4).

[Если при решении этой задачи рассмотреть отдельно случаи n=1 и n≠1, то можно показать, что

Помню как в мою бытность студентом на лекциях по алгебре наш профессор говорил: «Корень из трёх — это, примерно, 1,73; корень из двух — 1,41. Поэтому их сумма равна... (следовала пауза, необходимая для сложения этих чисел "в столбик") 3,14. А это есть?..» (он поворачивался к аудитории и сразу несколько человек говорили "пи") «Ну, вот», — с удовлетворением заключал профессор, выписывая окончательное "равенство": √3 + √2 = π.   :) — E.G.A.]

 3.  Найдите предел последовательности a_n = (√n² + 1 – n)n.

Преобразуем a_n так:

Теперь ясно, что a_n возрастает и стремится к пределу 1/2.

В противоположность предыдущему примеру здесь мы имеем дело с хорошим приближением: √n² + 1 – n < 1/2n.

 4 (M532).  Даны две последовательности a_n = √n+1 + √n  и  b_n = √4n+2. Докажите, что

а)   [a_n] = [b_n],

б)   0 < b_n – a_n < 1/16n√n.

В разности  b_n – a_n  появляется «тройная иррациональность»; к таким иррациональностям мы ещё вернёмся (см. задачу 8), но пока мы будем рассматривать √n+1 + √n = a_n как одно целое. Заметим, что величина a_n²=2n+1+2√n(n+1), очевидно, заключена между 4n+1 и 4n+2=b_n², поскольку n < √n(n+1) < n+1. Итак, мы уже получили a_n < b_n — левое неравенство в б). Кроме того, число b_n² = 4n+2, дающее при делении на 4 в остатке 2, не может быть полным квадратом (проверьте!), поэтому квадрат целого числа [b_n] не больше 4n+1; из неравенств [b_n] ≤ √4n+1 < a_n < b_n вытекает а). Теперь осталось оценить разность b_n – a_n сверху. Посмотрите, как здесь дважды работает переброска «сопряжённого» числа в знаменатель:

Заметим, что и эта оценка очень точная. Но убедиться в этом (и вообще исследовать поведение функции с многими радикалами) лучше уже не с помощью алгебраических преобразований, а средствами анализа — заменить переменную n на  h = 1/n  и воспользоваться формулой Тейлора √1 + h = 1 + h/2 – h²/8 + ... (См. [6].)

Мы уже говорили о пользе симметрии в геометрических задачах. Своего рода симметрией в  алгебре  является замена плюса на минус.

Так, если какое-либо выражение от √d равно  p + q√d  и мы всюду в этом выражении заменим √d на –√d, то естественно ожидать, что новое выражение окажется равным сопряженному числу  p – q√d. Мы будем пользоваться таким очевидным частным случаем этого свойства (a и b — рациональны, √d — нет):

 5.  Доказать, что уравнение

не имеет решений в рациональных числах x, y, z, t.

Можно, конечно, найти отдельно сумму членов левой части, не содержащих √5 (она должна быть равна 2), и отдельно — коэффициент при √5 (он должен равняться 1). Но что делать с полученной громоздкой системой неясно. Вместо этого воспользуемся (4) и заменим плюс перед √5 на минус!

Слева стоит неотрицательное число, справа — отрицательное.

 6.  Доказать, что существует бесконечно много пар (x; y) натуральных чисел, для которых x² отличается от 2y² на 1:

Несколько таких пар с небольшими (x; y) легко найти подбором: это (1; 1), (3; 2), (7; 5), (17; 12), ... (рис. 1). Как продолжить этот набор? Можно ли записать общую формулу для этих решений?

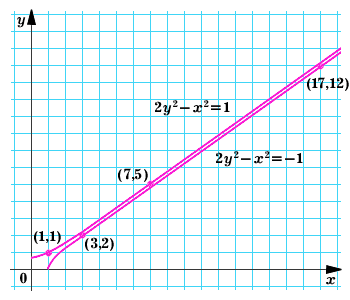Рис. 1.  Проходят ли эти гиперболы через бесконечное число узлов клетчатой бумаги?

Найти ответы на эти вопросы нам поможет число 1 + √2. Закономерность, позволяющая получать всё новые и новые решения (x; y), указана в таблице:

Видно, что коэффициенты x_n, y_n в числе

будут давать нужную пару. Доказать это поможет колонка таблицы из сопряжённых чисел (мы снова применяем (4)):

Перемножив два последних равенства, получим

и интересующее нас выражение попеременно равно то 1, то –1. Складывая и вычитая эти же два равенства, мы получим явное выражение для x_n и y_n:

Можно ли в решении этой задачи про целые числа обойтись без иррациональных чисел  1 + √2  и  1 – √2? Теперь, зная ответ, мы можем легко выразить (x_n+1; y_n+1) через предыдущую пару (x_n; y_n):  из  x_n+1 + y_n+1√2 = (x_n + y_n√2)(1 + √2) вытекает

До этого рекуррентного соотношения можно было, видимо, догадаться по нескольким первым решениям, а потом проверить, что

Добавив начальное условие x₁ = 1,   y₁ = 1, отсюда (по индукции) можно было бы заключить, что |x_n² – 2y_n²| = 1  для любого n. Далее, выразив обратно (x_n; y_n): через (x_n+1; y_n+1), «методом спуска» ([8]) можно доказать, что найденной серией исчерпываются все решения уравнения (5) в натуральных числах (x; y). Подобным же образом решается любое «уравнение Пелля» x² – dy² = c (а к уравнениям такого типа сводится любое квадратное уравнение в целых числах x, y), но у исходного уравнения может быть несколько серий решений ([7]).

Рекуррентные соотношения типа (6) возникают не только в теории чисел, но и в разных задачах анализа, теории вероятностей. Вот характерный пример комбинаторной задачи такого типа (она предлагалась на последней международной олимпиаде в Лондоне):

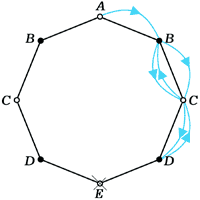
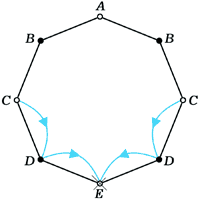
 7 (М595).  В вершине A правильного восьмиугольника сидит лягушка. Из любой вершины восьмиугольника, кроме вершины E, противоположной A, она может прыгнуть в любую из двух соседних вершин. Попав в E, лягушка останавливается и остаётся там. Найти количество e_m различных способов, которыми лягушка может попасть из вершины A в E ровно за m прыжков.

Если раскрасить вершины восьмиугольника через одну в чёрный и белый цвет (рис. 2), сразу станет ясно, что e_2k–1 = 0 при любом k: цвет вершин при каждом прыжке меняется. Обозначим через a_n и c_n количество способов, которым лягушка может за 2n прыжков, попасть из вершины A, соответственно, в вершину A и в одну из вершин C (из соображений симметрии ясно, что в каждую из вершин, обозначенных на рисунке буквой C, можно попасть одним и тем же числом способов). Как легко проверить (см. рис.2а,б,в,г),

А интересующее нас число e_2n равно, очевидно, 2c_n–1 (рис. 2д).

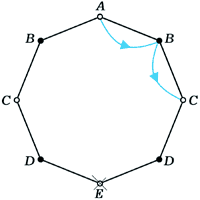а) c1 = 1

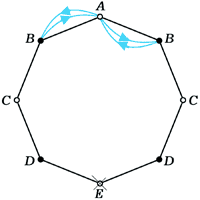б) a1 = 2

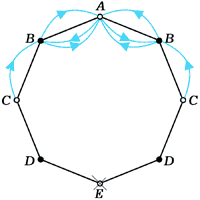в) an+1 = 2an + 2cn

г) cn+1 = an + 2cn

д) e2n = 2cn–1

Как же найти явную формулу для a_n и c_n? Запишем наше рекуррентное соотношение (7) так:

и — как вы уже, конечно, догадались — ещё так:

Отсюда по индукции, пользуясь (7), получаем:

Поэтому

а так как e_2n = 2c_n–1, получаем окончательно

 8 (М520).  Пусть

где q_n, r_n, s_n  и  t_n — целые числа. Найти пределы

lim   n → ∞

rn  qn

,

lim   n → ∞

sn  qn

,

lim   n → ∞

tn  qn

.

Конечно, мы здесь можем выразить (q_n+1; r_n+1; s_n+1; t_n+1) через (q_n; r_n; s_n; t_n), пользуясь тем, что

но, наученные опытом, мы уже знаем, что более простые формулы получаются не для самих чисел q_n, r_n, s_n, t_n, a для некоторых их комбинаций. Одну такую комбинацию мы уже знаем: это

Нетрудно сообразить, каковы будут другие. Рассмотрим вместе с данным числом

ещё три «сопряжённых»:

Тогда

Мы можем выразить q_n, r_n, s_n, t_n через λ₁, λ₂, λ₃, λ₄:

Теперь заметим, что λ₁ > |λ₂|, λ₁ > |λ₃|, λ₁ > |λ₄|. Поэтому

Аналогично найдём, что

Мы говорили выше, что сопряжённые числа a ± b√d возникают часто как корни  квадратного  уравнения с целыми коэффициентами. В связи с последней задачей возникает такое желание:

 9.  Написать уравнение с целыми коэффициентами, один из корней которого равен 1 + √2 + √3.

Возникает подозрение, что вместе с этим числом λ₁ уравнению с целыми коэффициентами удовлетворяют и сопряжённые, которые в решении предыдущей задачи мы обозначили λ₂, λ₃, λ₄. Нужное уравнение можно записать так:

то есть

после преобразований получаем

в предыдущей задаче. Заметим, кроме того, что мы на самом деле получили уравнение  наименьшей  степени (с целыми коэффициентами) с корнем λ₁ = 1 + √2 + √3. Попробуйте это доказать!

Мы разобрали несколько примеров, в которых затрагивались пограничные вопросы алгебры, математического анализа и теории чисел. (Каждому направлению, которое мы наметили, можно было бы посвятить более подробную статью в «Кванте»!) В заключение покажем ещё, как можно смотреть на основных героев статьи — «сопряжённые числа» — с чисто алгебраической точки зрения.

Предположим, что у нас есть множество P чисел (или выражений с буквами, или ещё каких-то элементов), с которыми можно выполнять четыре действия арифметики с соблюдением обычных арифметических правил. Такое множество называется полем; поля образуют, например, рациональные и действительные числа. Если в поле P не разрешимо, скажем, уравнение x² – d = 0, то можно  расширить  его, рассматривая элементы вида p + q√d, где p, q Î P, a √d — новый символ, который при умножении сам на себя дает d, т.е. √d·√d = d, так что

При d = –1 расширением поля вещественных чисел получаются комплексные числа.

В новом поле P₁ — «квадратичном расширении» поля P — есть интересное отображение λ = p + q√d → λ = p – q√d (своеобразная «алгебраическая симметрия»), называемое сопряжением, с такими свойствами:

1. Все элементы старого поля P переходят в себя;
2. Все равенства, содержащие арифметические операции, при этом отображении сохраняются:

Это отображение является частным случаем так называемых автоморфизмов Галуа расширения P₁ поля P.

В задачах 8 и 9 мы видели пример «двукратного» расширения — присоединения √2 и затем √3, — в результате которого получилось поле с бо́льшим количеством автоморфизмов Галуа: кроме тождественного отображения, их уже три

и их «взаимодействие» устроено так же, как во множестве самосовмещений прямоугольника.

Оказывается, к основному полю можно присоединять корни  любого  алгебраического уравнения. Автоморфизмы возникающего нового поля — предмет одной из красивейших ветвей алгебры XIX–XX века,  теории Галуа,  которая позволяет, в частности, исследовать вопрос о разрешимости уравнений в радикалах ([13], [14]).

Мы закончим эту статью набором задач, в основном продолжающих уже затронутые темы, но требующих иногда и новых соображений, и обещанным списком литературы.