Мне хотелось бы поговорить с вами об одной проблеме, которая, хотя сам я над ней и не работал, всегда меня чрезвычайно привлекала и которая очаровывала математиков, пожалуй, с доисторических времён и до наших дней, – а именно о проблеме распределения простых чисел.

Вам, конечно, известно, что простым числом называется отличное от 1 натуральное число, не делящееся ни на какие иные натуральные числа, кроме 1; во всяком случае, именно такое определение дают специалисты по теории чисел. Правда, другие математики иногда используют и иные определения. Так, для специалиста по теории функций простое число – это целочисленный нуль аналитической функции

Для алгебраиста – это

или

или

Для специалиста по комбинаторике простые числа определяются рекуррентной формулой [1]

						n
pn+1 =		1 – log 2	(	1 2	+	∑	∑	(–1)r 2  p i1 ...  p ir  – 1	)
						r = 1	1 ≤ i1 ≤ ... ≤ ir ≤ n

где [x] – целая часть числа x ⁴. И, наконец, логики определяют в последнее время простые числа как положительные значения многочлена [2]

F(a, b, с, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z) =
    = {k + 2} {1 – (wz + h + j – q)² – (2n + p + q + z – e)²
    – (a²y² – y² + 1 – x²)² – ({e⁴ + 2e³}{a + 1}² + 1 – o²)²
    – (16{k + 1}³{k + 2}{n + 1}² + 1 – f ²)²
    – ({(a + u⁴ – u²a)² – 1}{n + 4dy}² + 1 – {x + cu}²)²
    – (ai + k + 1 – l – i)²
    – ({gk + 2g + k + 1}{h + j} + h – z)²
    – (16r²y⁴{a² – 1} + 1 – u²)²
    – (p – m + l{a – n – 1} + b{2an + 2a – n² – 2n – 2})²
    – (z – pm + pla – p²l + t{2ap – p² – 1})²
    – (q – x + y{a – p – 1} + s{2ap + 2a – p² – 2p – 2})²
    – (a²l² – l² + 1 – m²)² – (n + l + v – y)²}.

[У Цагира в одной из скобок единичка пропущена. У Рибенбойма в книге «Рекорды простых чисел» приведён правильный вариант. Подробности ниже. Легко заметить, что по сути многочлен F — это произведение двух скобок: одна — это k + 2, другая — это единица минус куча квадратов. Поэтому только переменная k определяет значение простого числа, остальные переменные (и k вместе с ними) служат для отбрасывания составных чисел. Как только все квадраты занулятся, второй сомножитель в F станет равным единице и мы получим очередное простое число. — E.G.A.] Но я думаю, вы вполне удовлетворены первым из приведённых мной определений.

Имеются два главных факта о распределении простых чисел, о которых я надеюсь рассказать вам так, чтобы они навек запечатлелись в вашей памяти. Первый: простые числа, при своём таком простом определении и при своей роли кирпичиков, из которых строятся все натуральные числа ⁵, являются самыми капризными и упрямыми из всех объектов, вообще изучаемых математиками. Они растут среди натуральных чисел как сорная трава, не подчиняясь, кажется, ничему, кроме случая, и никто не может предсказать, где взойдет ещё одно простое, а, увидев число, – определить, простое оно или нет. Другой факт озадачивает ещё больше, так как он состоит в прямо противоположном утверждении, а именно: простые числа демонстрируют удивительную регулярность, они подчиняются законам, и притом с почти педантичной точностью.

Чтобы пояснить первое утверждение, я покажу вам список простых и составных чисел, не превосходящих 100 (табл. 1), причём, за исключением числа 2, приведены лишь нечётные числа, а затем список простых из ста натуральных чисел, предшествующих и следующих за 10 000 000 (табл. 2).

Полагаю, вы согласитесь, что нет явно видимой причины, по которой одно число является простым, а другое – нет. Напротив, при взгляде на эти таблицы возникает ощущение, будто стоишь перед непостижимой тайной творения. Что и математики до сих пор ещё не раскрыли эту тайну, пожалуй, наиболее убедительно подтверждает то усердие, с которым они и поныне ищут всё бóльшие простые. Для чисел, растущих закономерно, например для квадратов или степеней двойки, было бы, конечно, нелепо разыскивать экземпляр, превосходящий все известные. Для простых же чисел, напротив, прилагаются громадные усилия, чтобы именно это и сделать. Например в 1876 г. Люка доказал, что число 2¹²⁷ – 1 – простое [См. подробности в статье А. Н. Рудакова. — E.G.A.], и 75 лет оно оставалось наибольшим из известных простых чисел, что не покажется удивительным, если взглянуть на него:

Только в 1951 г. – после возникновения электронных вычислительных устройств – нашли бóльшее простое число. Сведения о сменявших друг друга числах-рекордсменах вы найдете в табл. 3 [3]. В настоящее время рекордсменом является 6002-значное число 2¹⁹⁹³⁷ – 1 (я бы не хотел его здесь выписывать); счастливчик, оно может гордиться своей славой ⁶. Кто сомневается в сказанном, может справиться в книге мировых рекордов Гиннесса.

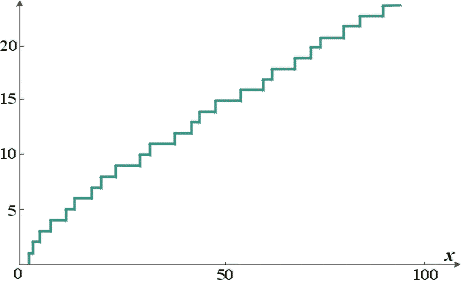
Однако гораздо интереснее вопрос о законах, которым подчиняются простые числа. Я привёл вам ранее в табл. 1 список простых чисел между 1 и 100. На рис. 1 та же информация представлена графически, функция π(x), о которой теперь пойдёт речь, выражает количество простых чисел, меньших или равных x; следовательно, в нуле она имеет значение 0 и скачком увеличивается на 1 в точках x = 2, 3, 5 и т.д., т.е. когда x равно простому числу. Уже из этого графика видно, что растёт π(x), несмотря на малые локальные колебания, в общем, довольно регулярно. Если же увеличить область изменения x до 50 000, то регулярность эта становится настолько отчётливой, что дух захватывает (рис. 2). По-моему, плавность, с которой поднимается эта кривая, следует отнести к числу удивительнейших фактов математики.

Рис. 1. Функция π(x) при x ≤ 100. Рис. 2. Функция π(x) при x ≤ 50000.

Но где закономерность, там и учёные, которые пытаются её разгадать. И данный случай не стал исключением. Нетрудно найти эмпирическую формулу, хорошо описывающую рост количества простых чисел. От 1 до 100 имеется 25 простых чисел, т.е. четверть всех чисел; до 1000 их 168, т.е. около одной шестой; до 10 000 их 1229, т.е. примерно одна восьмая. Продолжая вычисления до 100 000, 1 000 000 и т.д. и определяя каждый раз отношение количества простых к количеству всех натуральных чисел, получим данные, приведённые в табл. 4.

(Так скромно выписанные в ней значения π(x) потребовали тысяч часов трудоёмких вычислений.) Видно, что отношение x к π(x) при переходе от данной степени десяти к последующей всё время увеличивается примерно на 2,3. Математики сразу узнают в числе 2,3 логарифм 10 (разумеется, по основанию e). В результате возникает предположение, что

причём знак ~ означает, что отношение соединённых им выражений с ростом x стремится к 1. Это асимптотическое равенство, впервые доказанное в 1896 г., называется в настоящее время законом распределения простых чисел. Гаусс, величайший из математиков, открыл этот закон в пятнадцатилетнем возрасте, изучая таблицы простых чисел, содержавшиеся в подаренной ему за год до того таблице логарифмов. В течение всей своей жизни Гаусс живо интересовался распределением простых чисел и проводил обширные вычисления для выяснения этого вопроса. В своём письме к Энке [4] Гаусс описывает, как он «очень часто употреблял свободные четверть часа, чтобы то там, то здесь просчитать хилиаду» (т.е. интервал в 1000 чисел), и так до тех пор, пока он не нашёл, наконец, все простые, меньшие трёх миллионов (!), и не сравнил полученные результаты с предполагаемой формулой их распределения.

Рис. 3.

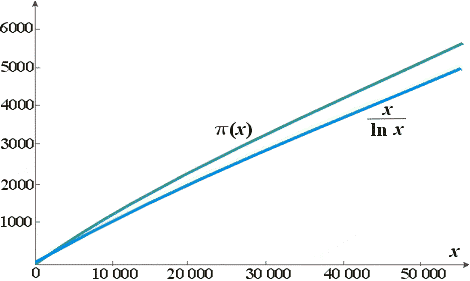
Закон распределения простых чисел утверждает, что функция π(x) асимптотически (т.е. с относительной погрешностью ⁷   0%) равна x/ln x. Однако если мы сравним графики функций x/ln x и π(x), то увидим, что, хотя функция x/ln x качественно и отражает поведение π(x), но всё же согласуется с ней не с такой точностью, которая позволила бы объяснить плавность графика π(x) (рис. 3). Итак, следует поставить вопрос о лучшем приближении. Посмотрев снова на таблицу отношений x/π(x), мы увидим, что это отношение почти точно равно ln x – 1. Проведя более тщательные и полные вычисления, Лежандр [5] в 1808 г. обнаружил, что особенно хорошее приближение получается, если вычесть из ln x не 1, а 1,08366, т.е.

Другое очень хорошее приближение π(x), впервые указанное Гауссом, можно получить, исходя из того эмпирически установленного факта, что плотность простых вблизи очень большого числа x почти точно равна 1/ln x. Поэтому количество простых чисел, не превосходящих x, приблизительно выражается логарифмической суммой

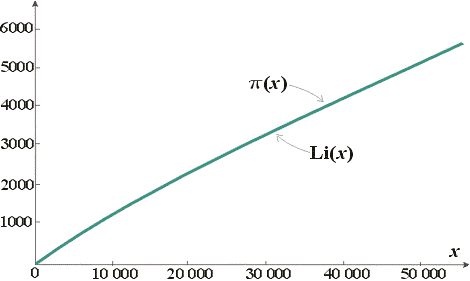
или, что примерно то же самое [6], интегральным логарифмом:

	x
Li (x) =	∫	dt  ln t	.
	2

Сравнивая графики Li(x) и π(x), приведённые на рис. 4, мы видим, что в рассматриваемом диапазоне в пределах точности рисунка они просто совпадают. Картинку для приближения Лежандра не стоит даже показывать, так как в указанном диапазоне значений x оно ещё лучше.

Рис. 4.

Существует ещё одно приближение функции π(x), о котором я хотел бы упомянуть. Исследования Римана по простым числам наводят на мысль, что вероятность того, что большое число x является простым, будет с большей точностью задаваться функцией 1/ln x, если учитывать не только сами простые, но и их степени, причём квадрат простого числа считать за половину простого, третью степень – за треть и т.д. Это приводит к следующему приближённому равенству:

или, если «обратить» эту зависимость

Функцию, стоящую в правой части последнего равенства, обозначим (в честь Римана) через R(x). Как видно из табл. 5, она представляет собой удивительно хорошее приближение к π(x).

Читателю, немного знакомому с теорией функций, могу сказать, что R(x) – целая функция от ln x, задаваемая быстро сходящимся степенным рядом

	∞
R(x) = 1 +	∑	1  nζ(n+1)	(ln x)n n!	,
	n = 1

где ζ(n) – дзета-функция Римана [8] ⁸.

Впрочем, надо подчеркнуть, что приближения Гаусса и Лежандра для π(x) были получены чисто эмпирически и что даже Риман, который пришёл к своей функции R(x) с помощью теоретических рассуждений, не доказал асимптотического закона распределения простых чисел. Это было сделано (на основе исследований Римана) лишь в 1896 г. Адамаром и (независимо) Валле Пуссеном.

Я хотел бы ещё привести несколько численных примеров, показывающих возможность предсказания фактов о простых числах. Как уже было отмечено, вероятность того, что число порядка x является простым, приблизительно равна 1/ln x; это означает, что количество простых в интервале длины a поблизости от x должно быть примерно равно a/ln x, во всяком случае если длина интервала достаточно велика, чтобы имело смысл заниматься статистикой, но достаточно мала по сравнению с величиной x. Например, в интервале между ста миллионами и ста миллионами плюс 150 000, следует ожидать появления около 8142 простых, так как

Соответственно вероятность того, что два заданных числа вблизи x оба окажутся простыми, приблизительно равна 1/ln² x. Поэтому ожидаемое количество простых чисел-близнецов (т.е. пар простых, отличающихся ровно на 2, вроде 11, 13 или 59, 61) в интервале от x до x+a приблизительно равно a/ln² x. На самом деле ожидаемая величина немного больше, поскольку если уже известно, что число n является простым, то это несколько изменяет шансы, что и n + 2 будет простым; например, n + 2 в этом случае заведомо нечётно. Несложные эвристические рассуждения [9] показывают, что ожидаемое количество простых чисел-близнецов в интервале [x, x+a] равно Ca/ln² x, где C – постоянная, приблизительно равная 1,3 (точнее C = 1,3203236316...). Так, между числами 100 000 000 и 100 150 000 должно быть примерно 1,32×150000/(18,427)² ≈ 584 простых чисел-близнецов. В табл. 6 я привожу полученные Джоунзом, Лэлом и Бландоном [10] данные о действительном количестве простых чисел и простых чисел-близнецов в этом и в некоторых других интервалах той же длины около больших степеней десяти. Видно, что реальные значения очень хорошо согласуются с ожидаемым результатом. Это особенно удивительно для простых-близнецов, так как пока не удается доказать даже тот факт, что их бесконечно много, не говоря уже об асимптотическом законе их распределения.

В качестве последнего примера на тему о предсказуемости свойств простых чисел упомяну ещё проблему о «провалах» между ними. Рассматривая таблицу простых чисел, можно заметить, что иногда встречаются особенно большие интервалы (например, между 113 и 127), совсем не содержащие простых. Пусть g(x) – длина наибольшего из интервалов между 1 и x, не содержащих простых чисел ⁹. Например, для x = 200 самым длинным из них является только что упомянутый интервал от 113 до 127, так что g(200) = 14. Величина g(x) растёт, разумеется, очень неравномерно, однако некоторые эвристические соображения [11] приводят к асимптотической формуле

Насколько всё-таки хорошо согласуется с ожидаемым поведением даже эта чрезвычайно сильно скачущая функция g(x), видно из рис. 5.

Рис. 5.

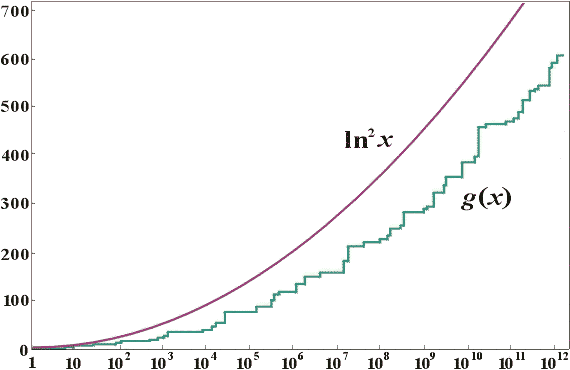
До сих пор я главное внимание уделял обоснованию утверждения о господствующем среди простых чисел порядке, нежели обоснованию утверждения об их своеволии. Кроме того, я ещё не показал, как было обещано в названии лекции, первые 50 миллионов простых, а привёл данные лишь о нескольких тысячах простых. Так вот, на рис. 6 графически представлена функция π(x) в сравнении с приближениями Лежандра, Гаусса и Римана при изменении x до 10 миллионов [12]; так как графики этих четырёх функций почти совпадают между собой (как мы это уже видели на рис. 4), то на рис. 6 приведены графики соответствующих разностей.

Рис. 6. Графики приближений Гаусса    , Лежандра     и Римана    ; значения x отложены в миллионах.

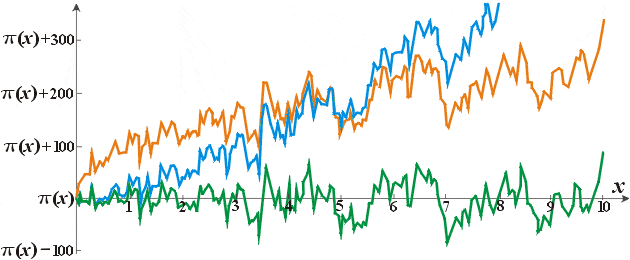
Думаю, уже одна эта картинка ясно показывает, чтó ожидает того, кто решается изучать простые числа.

Как видно из рисунка, приближение Лежандра x/(ln x – 1,08366) при небольших x (примерно до 1 миллиона) значительно точнее приближения Гаусса Li(x), однако начиная с 5 миллионов точнее становится Li(x) и можно показать, что с дальнейшим ростом x это становится всё вернее.

До 10 миллионов имеется примерно 600 000 простых чисел. Чтобы представить все обещанные 50 миллионов простых, следует дойти до 1 миллиарда. График разности R(x) – π(x) в этой области показан на рис. 7 [13]. Колебания функции R(x) – π(x) становятся с ростом x всё более сильными, однако не превосходят нескольких сотен даже при таких, почти невообразимо больших x.

Рис. 7. График разности R(x) – π(x) на интервале 0 ≤ x ≤ 1 000 000 000.

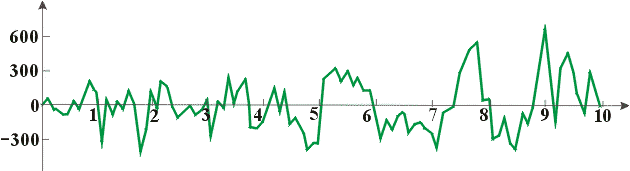
Здесь можно упомянуть ещё один факт о функции π(x). На рис. 6 приближение Гаусса Li(x) всюду больше π(x), и это остаётся справедливым и до 1 миллиарда, как явствует из рис. 8 (на котором данные отложены в логарифмических шкалах ¹⁰).

Рис. 8. Значения x отложены в миллионах.

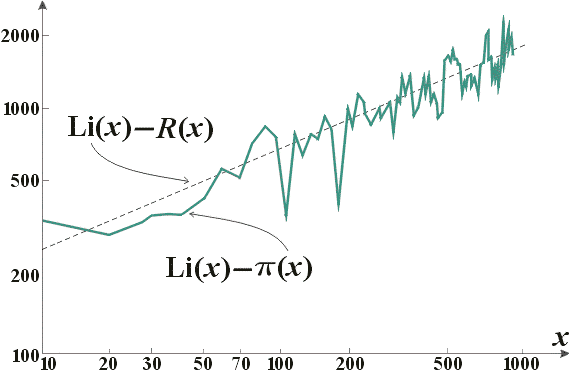
Последний график, несомненно, создает впечатление, что разность Li(x) – π(x) с ростом x стремится к бесконечности, т.е. что интегральный логарифм Li(x) принципиально переоценивает количество простых, не превосходящих x (и так как R(x) всегда меньше Li(x), то это соответствовало бы утверждению, что R(x) даёт лучшее приближение, чем Li(x). Однако дело обстоит иначе. Можно доказать, что существуют точки, в которых π(x) изменяется настолько резко, что становится больше Li(x). Такие числа до сих пор не найдены и, может быть, никогда и не будут найдены, но Литтлвуд доказал, что они существуют, а Скьюз [14] установил даже, что одно из них не превосходит

1010

1034

.

(По поводу этого числа Харди заметил, что оно, пожалуй, наибольшее из всех, когда-либо служивших в математике какой-нибудь определённой цели.) Во всяком случае, это убедительно показывает, как неразумно делать выводы о свойствах простых, основываясь только на численных данных.

В последней части моего сообщения я хочу рассказать о некоторых теоретических результатах, касающихся π(x), чтобы у вас не сложилось впечатление, будто исследования по простым числам следует отнести исключительно к области экспериментальной математики. Непосвящённому может показаться, что свойство числа быть простым слишком случайно и исключает возможность доказательства каких-либо фактов о таких числах. Этот взгляд был опровергнут уже 2200 лет тому назад Евклидом, доказавшим существование бесконечного множества простых чисел. Его рассуждение укладывается в одну фразу: если бы имелось лишь конечное число простых, то можно было бы их перемножить и, прибавив единицу, получить число, которое не делится ни на одно простое, что невозможно. В XVIII веке Эйлер доказал более сильное утверждение, а именно что ряд, составленный из величин, обратных простым, расходится, т.е. его частичные суммы ¹¹ становятся с ростом количества слагаемых больше любого заданного числа. В его (также очень простом ¹²) доказательстве была использована функция

роль которой для изучения π(x) была полностью оценена лишь позднее, благодаря работам Римана. В этой связи стоит отметить, что, хотя сумма величин, обратных всем простым, бесконечна, однако сумма величин, обратных всем известным простым (т.е. примерно первым 50 миллионам), меньше четырёх [15].

Только в 1850 г. Чебышёву удалось сделать первый шаг к доказательству закона распределения простых чисел [16]. [«Чебышёв – лидер русских математиков – имел необъяснимую неприязнь к теории функций комплексного переменного и к комплексным числам вообще. ... Эта нелюбовь Чебышёва к комплексным числам вышла ему, так сказать "боком": асимптотический закон распределения простых чисел, к выводу которого Чебышёв подошёл ближе всех, был впервые доказан Валле-Пуссеном и Адамаром именно средствами комплексного анализа.» – цитата из статьи «Софья Ковалевская: математик и человек», УМН, № 6 (2000). — E.G.A.] Он показал, что при достаточно больших x справедлива оценка

т.е. что закон распределения простых чисел справедлив с относительной погрешностью, не превосходящей 11%. Его доказательство, использующее биномиальные коэффициенты ¹³, так красиво, что я не могу устоять перед искушением привести его упрощённый вариант (разумеется, ввиду этого, с несколько худшими постоянными).

Покажем, что выполняется такая оценка сверху:

Она непосредственно проверяется для x < 1200. Будем рассуждать по индукции ¹⁴ и предположим, что наша оценка доказана для всех x ≤ n. Рассмотрим «центральный» биномиальный коэффициент

(

2n n

)

.

Поскольку

22n = (1 + 1)2n =

(

2n 0

)

+

(

2n 1

)

+ ... +

(

2n n

)

+ ... +

(

2n 2n

)

,

он, безусловно, меньше 2²ⁿ. С другой стороны,

Каждое простое число p, меньшее 2n, входит в числитель, но, если p больше n, не входит в знаменатель. Поэтому «центральный» биномиальный коэффициент делится на каждое простое, лежащее между n и 2n: ¹⁵

В произведении слева π(2n) – π(n) сомножителей, каждый из которых больше n, поэтому

Прологарифмировав, получим

Согласно предположению индукции, теорема верна для n, т.е.

Складывая два последних неравенства, находим, что

т.е. теорема верна и для 2n. Так как

то она справедлива и для 2n + 1, чем и завершается шаг индукции.

Для получения оценки снизу нам понадобится следующая простая лемма, которая легко выводится из известной формулы для показателя степени простого числа, с которым оно входит в n! [17]:

ЛЕММА. Пусть р – простое число. Если p^v(p) – наибольшая степень р, которая входит в

(

n k

)

,

то p^v(p) ≤ n.

СЛЕДСТВИЕ. Для любого биномиального коэффициента

(

n k

)

справедлива оценка

(	n k	)	=	∏	pv(p) ≤ nπ (n)	.
				p ≤ n

Применив утверждение этого следствия ко всем биномиальным коэффициентам с заданным n и сложив полученные неравенства, найдём

	n
2n = (1 + 1)n =	∑	(	n k	)	≤ (n + 1)·nπ (n)	,
	k = 0

или, после логарифмирования,

В заключение я хочу сказать несколько слов о результатах Римана. Хотя Риман и не доказал асимптотического закона распределения простых чисел, зато он сделал нечто гораздо более удивительное – дал точную формулу для π(x). Эта формула выглядит так:

где суммирование идёт по корням дзета-функции ζ(s) [18]. Корни эти (помимо так называемых «тривиальных корней» p = –2, –4, –6..., вкладом которых в общую сумму можно пренебречь) являются комплексными числами с вещественной частью, заключённой между 0 и 1; первые 10 из них таковы [19]:

Легко показать, что вместе с каждым ρ в число корней дзета-функции обязательно входит и комплексно-сопряжённое с ним число. А вот знаменитая гипотеза Римана, что вещественная часть корня всегда в точности равна 1/2, ещё никем не доказана, хотя её доказательство имело бы для теории простых чисел в высшей степени важное значение [20]. В настоящее время гипотеза проверена для 7 миллионов корней.

С помощью введённой выше функции R(x) формулу Римана можно записать в виде

Это дает в качестве k-го приближения к π(x) функцию

– слагаемое, отвечающее n-й паре корней дзета-функции; T_n(x) при любом n является гладкой осциллирующей функцией от x. Графики T_n(x) для первых значений n показаны на рис. 9 [21].

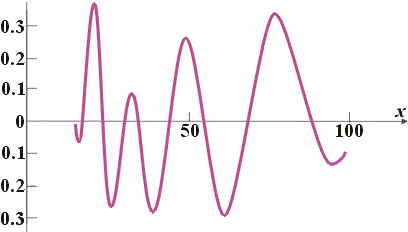Вместе с T_n(x) и R_k(x) является гладкой функцией при любом k. С ростом k эта функция приближается к π(x). В качестве иллюстрации на рис. 10 приведены графики 10-го и 29-го приближений, а также для сравнения график π(x) на интервале от 0 до 100 (см. рис. 1).

Я надеюсь, что после моего рассказа у вас осталось некоторое впечатление о замечательной красоте простых чисел и о тех неисчислимых сюрпризах, которые они нам готовят.

Примечания

[1]	J.M.Gandhi, Formulae for the n-th prime, Proc. Washington State Univ. Conf. on Number Theory, Washington State Univ., Pullman, Wash., 1971, 96-106. назад к тексту
[2]	J.P.Jones, Diophantine representation of the set of prime numbers, Notices of the AMS 22 (1975), A-326. назад к тексту
[3]	К тому что так много чисел из этого списка имеют вид Mk = 2k – 1, существует веская причина: согласно одной теореме, восходящей к Люка, число Мk (k ≥ 2) тогда и только тогда является простым, когда оно делит число Lk–1, где числа Ln определяются рекуррентным соотношением: L1 = 4, Ln+1 = Ln2 – 2 (так что L2 = 14, L3 = 194, L4 = 37634, ...) и, таким образом, простоту Mk проверить значительно легче, чем простоту других чисел того же порядка. Простые вида 2k – 1 (в этом случае k само обязательно должно быть простым) называются простыми числами Мерсенна (по имени французского математика, который в 1644 г. указал в большей своей части верный список всех таких простых, меньших 1079). Числа Мерсенна играют важную роль и в некоторых других проблемах теории чисел. Евклид обнаружил, что если число 2p – 1 – простое, то число 2p–1(2p – 1) является «совершенным», т.е. равно сумме своих собственных 16 делителей (например, 6 = 1 + 2 + 3, 28 = 1 + 2 + 4 + 7 + 14, 496 = 1 + 2 + 4 + 6 + 16 + 31 + 62 + 124 + 248), а Эйлер доказал, что все чётные совершенные числа имеют указанный вид. Неизвестно, существуют ли вообще нечётные совершенные числа; во всяком случае, такие числа должны быть больше 10100. Имеется ровно 24 значения р < 20 000, при которых число 2p – 1 – простое. назад к тексту
[4]	С.F.Gauss, Werke, II, 1872, 444–447. Обсуждение истории вопроса о приближениях π(x) см., например, в статье L.J.Goldstein, A history of the prime number theorem, Amer. Math. Monthly 80 (1973), 599–615. назад к тексту
[5]	A.M.Legendre, Essai sur la théorie des Nombres, Paris, 1808, стр. 394. назад к тексту
[6]	Точнее, имеют место неравенства Ls(x) – 1,5 < Li(x) < Ls(x) т.е. разность Li(x) и Ls(x) ограничена. Отметим, что в настоящее время интегральный логарифм обычно понимается в смысле главного значения:   x   1 – ε   x   li (x) = V.P. ∫ dt ln t  =  lim ( ∫ dt ln t  +  ∫ dt ln t ) ;   0   ε → 0   0   1 + ε   однако это определение отличается от приведённого в тексте лишь на константу. назад к тексту
[7]	Коэффициент при Li(x1/n) определяется следующим образом: он равен +1/n, если n есть произведение чётного числа различных простых, равен –1/n, если n – произведение нечётного числа различных простых, и равен 0, если n делится на квадрат какого-нибудь простого. назад к тексту
[8]	Эту функцию можно представить и по-другому:   ∞   R (x) =  ∫  (ln x)t dt t Γ(t + 1) ζ(t + 1)   0   (ζ(s) – дзета-функция Римана, Γ(s) – гамма-функция) или R (e2πx) @  2 π { 2 B2 x +  4 3B4 x3 +  6 5B6 x5 + ...  } =  2 π { 12x + 40x3 +  252 5 x5 + ...  } (Bk – это k-е число Бернулли; знак @ означает, что разность соединённых таким знаком выражений стремится к 0 с ростом x); оба представления указал Рамануджан. См. G.H.Hardy, Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, Cambridge University Press, 1940, гл.2. назад к тексту
[9]	А именно: для пары (m, n) случайно выбранных чисел вероятность того, что m и n оба не сравнимы с 0 по модулю p 17, очевидно, равна ((p – 1)/p)2, а для одного случайно выбранного числа n вероятность того, что n и n + 2 оба не сравнимы с 0 по модулю p, равна 1/2 при р = 2 и (p – 2)/p при p ≠ 2. Поэтому вероятность того, что n и n + 2 представляют собой пару «кандидатов в простые по модулю p», отличается от соответствующей вероятности для двух независимых чисел m и n множителем p – 2 p  ·  p² (p – 1)² при p ≠ 2 и множителем 2 при p = 2. Таким образом, интересующая нас вероятность отличается от указанной в тексте наличием множителя C = 2 ∏ p² – 2p p² – 2p + 1  = 1,32032... .   p > 2 p – простое   Несколько более тщательно эти рассуждения проведены в книге: G.H.Hardy, Е.М.Wright, An Introduction to the Theory of Numbers, 5th ed., Oxford, 1979, § 22.20, стр. 371–373. назад к тексту
[10]	М.F.Jones, M.Lal, W.J.Blundon, Statistics on certain large primes, Math. Comp. 21 (1967), 103–107. назад к тексту
[11]	D.Shanks, On maximal gaps between successive primes, Math. Comp. 18 (1964), 646–651. График g(x) построен с использованием таблиц, приведённых в следующих работах: L.J.Lander, T.R.Parkin, On first appearance of prime differences, Math. Comp. 21 (1967), 483–488. R.P.Brent, The first occurrence of large gaps between successive primes, Math. Comp. 27 (1973), 959–963. назад к тексту
[12]	Данные для этого графика взяты из таблицы простых чисел Лемера: D.N.Lehmer, List of Prime Numbers from 1 to 10006721, Hafner Publishing Co., New York, 1956. назад к тексту
[13]	Этот и следующий графики построены по значениям π(x), приведённым в статье D.C.Mapes, Fast method for computing the number of primes less than a given limit, Math. Comp. 17 (1963), 179–185. В отличие от данных Лемера, использованных при построении предыдущего графика, эти значения вычислены по одной из формул π(x), а не путём непосредственного подсчёта простых, не превышающих x. назад к тексту
[14]	S.Skewes, On the difference π(x) – li (x). I, J. Lond. Math. Soc. 8 (1933), 277–283. Приведённую оценку Скьюз сперва доказал в предположении справедливости обсуждаемой далее в тексте гипотезы Римана. Через 22 года он же: S.Skewes, On the difference π(x) – li (x). II, Proc. Lond. Math. Soc. (3)5 (1955), 48–70. не используя этой гипотезы, доказал, что существует x, не превосходящее (ещё намного большего) значения 1010 10 964 , для которого π(x) > Li(x). Эта граница была заменена Коэном и Мейхью на 1010 529,7 , а Леманом: Е.Lehman, On the difference π(x) – li (x), Acta Arithm. 11 (1966), 397–410. на 1,65·101165. Леман даже показал, что между 1,53·101165 и 1,65·101165 имеется интервал, содержащий по меньшей мере 10500 чисел, на котором π(x) больше Li(x). Согласно его исследованиям, очень вероятно, что имеется число x, близкое к 6,663·10370, для которого π(x) > Li(x) и нет ни одного числа, меньшего 1020, с тем же свойством. назад к тексту
[15]	Вообще, имеет место соотношение (предположенное в 1796 г. Гауссом и доказанное в 1874 г. Мертенсом): ∑  1  p   =  ln ln x + C + ε(x), p < x   где ε(x) → 0 при x → ∞ и C – константа, приблизительно равная 0,261497. Это выражение при x = 109 меньше 3,3 и даже при x = 1018 ещё не превосходит 4. [Относительно сходимости рядов по простым числам имеет место любопытная Теорема (Чебышёв): Если при x ≥ x0 функция F(x) положительна и F(x)/ln x монотонно убывает, то ряды ∞ ∑  F(p)     и     ∑  F(n) ln n p n=2 сходятся или расходятся одновременно. Например, ряд ∑ 1/(p ln p) сходится и его сумма равна 1,63 ± 0.01, тогда как его «натуральный» собрат ∑ 1/(n ln n) расходится. — E.G.A.] назад к тексту
[16]	П.Л.Чебышёв, Recherches nouvelles sur les nombres premiers, Paris 1851, С. R. Paris 29 (1849), 397–401, 738–739. Современное изложение доказательства Чебышёва см. в книге: А.А.Бухштаб, Теория чисел. М.: Просвещение, 1966.назад к тексту
[17]	Наибольшая степень p, которая делит n!, есть   [ n  p ]  +  [ n  p² ]  + ...    p   , где [x] обозначает целую часть числа x – наибольшее целое, не превосходящее x; поэтому в обозначениях леммы v(p) =  ∑ { [  n  pr ]  –  [  k  pr ]  –  [  n – k pr ] }.   r ≥ 1   В этой сумме каждое слагаемое равно 0, или 1, причём заведомо равно 0 при r >   ln n  ln p (так как тогда [n/pr] = 0). Значит, v(p) ≤  [  ln n  ln p ]  , откуда и следует утверждение леммы. назад к тексту
[18]	Указанное ранее определение ζ(s) в виде ряда 1 +  1 2s  +  1 3s  + ... имеет смысл лишь тогда, когда s – комплексное число, вещественная часть которого больше 1 (ибо только при таком условии ряд будет сходящимся), и в этой области ζ(s) не имеет нулей. Функцию ζ(s) можно, однако, доопределить для всех комплексных чисел и рассматривать её корни в комплексной плоскости. Расширение области определения ζ(s) до полуплоскости Re(s) > 0 получается особенно просто, если воспользоваться справедливым при Re(s) > 1 тождеством (1 – 21–s)ζ(s) = 1 +  1 2s  +  1 3s  + ... – 2 ( 1 2s  +  1 4s  +  1 6s  + ... )  = 1 –  1 2s  +  1 3s  – ... и заметить, что стоящий справа ряд сходится при всех s, имеющих положительную вещественную часть. Отсюда легко вывести, что «интересные» корни дзета-функции, т.е. корни вида ρ = β + iγ, 0 < β < 1, задаются двумя уравнениями ∞     ∞   ∑ (–1)n – 1 nβ cos(γ ln n) = 0,   ∑ (–1)n – 1 nβ sin(γ ln n) = 0. n = 1     n = 1   Ряд по корням ρ в формуле Римана сходится неабсолютно, и поэтому его члены следует располагать в надлежащем порядке (по возрастанию абсолютного значения Im(ρ)). Наконец, отметим, что точная формула для π(x) была найдена Риманом ещё в 1859 г., а доказана Мангольдтом лишь в 1895 г. назад к тексту
[19]	Эти корни уже в 1903 г. вычислил Грам: J.-P.Gram, Sur les zéros de la fonction ζ(s) de Riemann, Acta Math. 27 (1903), 289–304. Очень удачное изложение теории дзета-функции Римана и методов вычисления её нулей дано в книге: H.M.Edwards, Riemann's Zeta Function, Academic Press, New York, 1974. назад к тексту
[20]	А именно, из гипотезы Римана вытекает следующее утверждение (верно и обратное): погрешность приближения π(x) функцией Li(x) не превосходит C√x ln x, где C – некоторая постоянная; в то же время неизвестно, меньше ли эта погрешность xc при каком-нибудь с < 1. назад к тексту
[21]	Этот график, как и три последующих, заимствован из работы: H.Riesel, G.Göhl, Some calculations related to Riemann's prime number formula, Math. Comp. 24 (1970), 969–983. назад к тексту

Добавление

Так как приведённый выше текст, представляющий собой точную запись моей вступительной лекции, уже был опубликован ранее (Elemente der Mathematik, Beiheft № 15, 1977 [английский перевод: Mathematical Intelligencer 0 (1977), 7–19]), я почёл за лучшее не пытаться «осовременить» текст, а оставив его без изменений, упомянуть результаты новейших исследований в этом коротком добавлении.

1. К списку необычных определений простых чисел, с которого мы начали наше путешествие, следует добавить еще одно, на этот раз из теории игр. А именно (по Конвею), отправляясь от N = 2, на каждом шаге мы заменяем N на αN, где α – первое из четырнадцати рациональных чисел

для которого число αN – целое. Для получающейся при этом последовательности 2, 15, 825, 725, 1925, ... все фигурирующие в ней степени двойки будут иметь вид 2^p, где р – простые, идущие в своём естественном порядке! С помощью хорошего калькулятора можно таким путем за несколько минут отыскать первые 4 или 5 простых чисел.

2. С 1971 г. уже три раза был побит мировой рекорд наибольшего известного простого числа; по указанной в примечании 3 причине каждый раз это было снова число Мерсенна 2^p – 1, а именно с p = 21 701, 23 209 и 44 497 ¹⁸.

3. Данные о количестве простых и простых-близнецов (табл. 6) теперь имеются до 10¹¹:

R.Brent, Tables concerning irregularities in the distribution of primes and twin primes to 10¹¹, 12 computer sheets deposited in UMT File 21, Review in Math. Comp. 30 (1976) 379.

Особенно интересна с этой точки зрения статья

R.Е.Grandall, M.A.Penk, A search for large twin prime pairs. Math. Comp. 33 (1979), 383–388.

В ней не только указана наибольшая известная пара близнецов (по 303 цифры в каждом!), но и описана статистическая проверка асимптотической формулы

для 132947 случайно выбранных чисел от 10⁴⁹ до 10⁵⁴ при ожидаемых 245±25 парах близнецов фактически было найдено 249 пар. В настоящее время и о функции «провалов» g(x) имеется больше данных, чем показано на рис. 5; см.

R.Brent, The distribution of prime gaps in intervals up to 10¹⁶, Review in Math. Comp. 28 (1974), 331.

В качестве ещё одного примера нерегулярности распределения простых чисел следует упомянуть результат Бейза и Хадсона о разности Δ(x) = π_4,3(x) – π_4,1(x):

С.Bays, R.Hudson, Math. Comp. 32 (1978), 281–286.

(π_a,b(x) обозначает число простых вида an + b, не превосходящих x). Эта разность, которая при малых x всегда положительна и при всех x очень мала (так, π_4,1(10¹⁰) = 227 523 275, а π_4,3(10¹⁰) = 227 529 235), согласно результатам Бейза и Хадсона, остаётся положительной до x = 950 000 000, за исключением менее чем одной тысячи значений, однако до x = 2·10¹⁰ есть очень большой интервал [1,854·10¹⁰, 1,895·10¹⁰], на котором она отрицательна, и её минимум в этой области равен Δ(18 699 356 297) = –2719.

4. Гипотеза Римана проверена уже для 150 миллионов корней, а именно для всех ρ, у которых |Im ρ| < 32 585 736,4. См.

R.Brent, On the zeros of the Riemann zeta function in the critical strip. Math. Comp. 33 (1979), 1361–1372.

[Я хотел бы добавить к рассказу Д. Цагира ещё несколько фактов. В 1988 г. вышла «Книга рекордов в области простых чисел» Рибенбойма. Мне не довелось её полистать, но рецензия на неё, опубликованная в «Бюллетене Американского математического общества», даёт некоторое представление о затрагиваемых вопросах и служит хорошим дополнением к вышеизложенному.

С появлением Колхоза, Гигапедии и сервисов типа Rapidshare возможности для поиска и обретения требуемой физ-мат литературы кардинально изменились, причём в лучшую сторону. Теперь доступны и дайджест книги Рибенбойма на русском языке, опубликованный в УМН, 1987, № 5, с. 119–176 и третье издание «The New Book of Prime Number Records», вышедшее в издательстве Шпрингера в 1996 году. Я выкладываю их у себя на сайте, чтобы интересующиеся не утруждали себя составлением запросов к нашим и не нашим поисковикам. Кроме того, я поправил в файлах те опечатки, которые за время, прошедшее после выхода книги, обнаружили дотошные читатели. Но на самом деле причиной для выклада стало ощущение непостижимой бездны, которое складывается уже после прочтения первых страниц статьи в УМН. — E.G.A.]