
И. М. Яглом. ГЕРМАН ВЕЙЛЬ.
Издательство «ЗНАНИЕ», Москва, 1967. 48 с.
I II III IV V VI
Цитируемые работы Г. Вейля
Примечания
 |
ПоказатьСкрыть нумерацию страниц
И. М. Яглом. ГЕРМАН ВЕЙЛЬ. Издательство «ЗНАНИЕ», Москва, 1967. 48 с. I II III IV V VI Цитируемые работы Г. Вейля Примечания |
Эта брошюра (в основу которой положена вступительная статья автора к указанной на стр.18 книге «Симметрия» Г. Вейля) рассказывает об одном из самых замечательных математиков
Небольшой объём брошюры и ориентация на малоподготовленного читателя заставили отказаться от попытки всестороннего освещения вклада Г. Вейля в современную математику — так, например, здесь ничего не говорится о работах этого выдающегося специалиста в области математического анализа и лишь в самых общих словах упоминается об исследованиях Вейля в области оснований математики, которым сам автор придавал весьма большое значение. Но математические работы вообще трудно описывать; гораздо больше может дать их изучение, — и автор настоящей брошюры будет очень рад, если чтение её послужит стимулом к изучению оригинальных книг и статей Вейля, целый ряд которых переведён на русский язык (книги [3], [11], [18] и [45]; статьи [2], [34] и частично [35] из приведённого в конце брошюры списка).
Содержание брошюры неоднократно обсуждалось с А. М. Ягломом, которого я рад поблагодарить за конструктивную критику и ценные советы. Я благодарен также В. Л. Вишняку, выполнившему по моей просьбе перевод стихотворного эпиграфа к книге Вейля «Пространство, время, материя».
| Южно-Сахалинск, апрель 1967 года |
И. М. Яглом |
В Библии, на одной из первых страниц этой древней книги, рассказана следующая легенда. Когда людей стало много, а науки и искусства достигли значительного развития, решили люди, что доступно им всё. И в ознаменование этого построили они город — его позже назвали Вавилон, — а в центре города — башню. И так как могли люди много, то башню захотели они возвести высокую — до небес. Наблюдал это бог в небе — и испугался: а вдруг и впрямь доберутся люди с башней вавилонской своей до неба, до бога? И разделил он языки — а до этого все люди говорили на одном языке — и перестали люди понимать друг друга. Ни одного мудрого полиглота, который смог бы объяснить всем общий замысел строения, не нашлось на земле — и рассыпалась башня, ибо нельзя строить что-либо совместно, не понимая друг друга.
Высоко вознеслась гордая башня современной математики.
И всё же...
Герман Вейль (Hermann Weyl) родился 9 ноября 1885 г. в Германии, в небольшом местечке Эльмсхорн вблизи Гамбурга. По окончании в 1904 г. средней школы он поступил в знаменитый Гёттингенский университет, который бесспорно являлся в те годы центром мировой математической мысли. В Гёттингене Г. Вейль провёл ряд лет, которые были определяющими для становления его как учёного. Окончил он университет в 1908 г. и в том же году защитил диссертацию и получил степень доктора философии. С 1908 до 1913 г. приват-доцент Вейль читал лекции в Гёттингенском университете; лишь один из этих годов он провёл в Мюнхене, где работал тогда один из любимых учеников гёттингенского профессора Феликса Клейна физик и математик Арнольд Зоммерфельд, научные интересы которого имели много точек соприкосновения с интересами Вейля. Только в 1913 г. Г. Вейль покинул надолго Гёттинген, приняв предложенное ему место профессора знаменитого Высшего технического училища в г. Цюрихе (Швейцария).
В Гёттингенском университете в годы пребывания там Вейля царили Феликс Клейн и Давид Гильберт, — и учёба у этих двух крупнейших учёных сыграла огромную роль в жизни Вейля. Непосредственным учителем Вейля был Д. Гильберт: ведь причиной поступления Вейля в Гёттингенский университет явилось то случайное обстоятельство, что директор 6 средней школы, в которой учился Вейль, был двоюродным братом Гильберта и направил одарённого школьника к своему знаменитому кузену (и этой случайности Гильберт обязан лучшим из своих учеников, а Вейль, возможно, всей своей поразительной научной карьерой!).
Д. Гильберту посвящено несколько статей Г. Вейля [7], из числа которых особо надо отметить обстоятельный обзор «Давид Гильберт и его математическое творчество», содержащий выразительный портрет Гильберта как человека и учёного. В годы учёбы Вейля в Гёттингене Гильберт разрабатывал те вопросы математического анализа, которые окончательно привели его к глубокой концепции (бесконечномерного!) пространства, «точками» которого являются функции; сегодня это пространство мы называем «гильбертовым пространством». К этому же кругу идей примыкают первые печатные работы Вейля [8], написанные им ещё в студенческие годы, — основным для этих работ как раз и является характерное для школы Гильберта представление о функциях как о «векторах» бесконечномерного метрического пространства функций, с выделением (и в этом, по-видимому, состоит первый самостоятельный вклад Г. Вейля в математическую науку) той роли, которую играют в пространстве функций «ортогональные функции», родственные ортогональным (перпендикулярным) векторам в обычном пространстве. К той же тематике относится и докторская диссертация Г. Вейля [9], посвящённая сингулярным (особым) интегральным уравнениям, а также ряд его важных работ
Да, и Клейна тоже. Влияние на молодого Вейля знаменитого Феликса Клейна также проходит красной нитью через всю жизнь и научную карьеру Вейля. Конечно, Г. Вейль не мог слушать курса Ф. Клейна по теории римановых поверхностей, относящегося ещё к
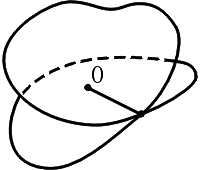
Рис. 1.
Основная идея книги [12] состоит в определённом синтезе развиваемых Ф. Клейном идей теории функций и топологических идей, идущих от появившегося в том же 1911 г. глубокого мемуара голландца Л. Брауэра — математика, которого Г. Вейль чрезвычайно высоко ценил. Использование топологических соображений позволило уточнить общее понятие «поверхности», нетривиальность которого хорошо иллюстрируется на примере достаточно сложно устроенных (многолистных) «поверхностей Римана», являющихся областями определения функций комплексного переменного (на обыкновенной плоскости не однозначных, а значит — не функциях!): если в области вещественных чисел, скажем, функцию
Однако влияние Ф. Клейна сказалось далеко не только в первой книге молодого Вейля. В противоположность Д. Гильберту, гордо именовавшему себя «чистым» математиком, для Ф. Клейна был характерен глубочайший интерес к физике и к физическим проблемам: недаром одна из первых книг Клейна, написанная в сотрудничестве с уже упоминавшимся А. Зоммерфельдом, была посвящена теории волчка. И для научной карьеры Вейля всегда был типичен тот сплав чисто математических и физических увлечений, при котором математические построения являются фундаментом для содержательных физических теорий, а физические соображения зачастую являются основополагающими для изящных математических конструкций. Наконец — и это наиболее важно отметить, рассказывая о всём научном пути Вейля, — Ф. Клейн прославился своей общей концепцией геометрии, в основу которой положено учение об «автоморфизмах» соответствующей геометрической теории — геометрических преобразованиях, сохраняющих все рассматриваемые в этой геометрии свойства фигур3. И эта концепция, по существу связывающая предмет геометрии с идеей симметрии, была глубоко продумана Г. Вейлем и послужила основой для некоторых из самых интересных его работ (подробнее об этом мы расскажем в дальнейшем).
Ф. Клейну посвящена вдохновенная речь [13] Г. Вейля, прочитанная в декабре 1929 г., через четыре года после смерти Клейна, на торжественном заседании Гёттингенского математического общества; эта замечательная речь не в меньшей степени характеризует того, кто её произнёс, чем того, кому она была посвящена. В начале своей речи Вейль цитирует слова Ф. Клейна о К. Ф. Гауссе, который «соединял величайшие успехи в каждой конкретной области математики с колоссальной разносторонностью и огромную творческую силу в чистой математике с практической смёткой в вопросах применения математики», и говорит, что эта характеристика вполне может быть отнесена к самому Клейну, — но ведь и для Г. Вейля не в меньшей мере характерно соединение глубины и разносторонности, владение всем арсеналом 9 средств чистой математики и серьёзный интерес к вопросам математического естествознания и даже техники. Далее Вейль подробно характеризует «научный стиль» Клейна, который всюду и везде оставался по преимуществу математиком, — даже в своей книге по теории волчка, даже в замечательной монографии по теории алгебраических функций, в предисловии к которой он заявляет, что писал эту книгу «почти как физик», и в которой для доказательства основных теорем существования для римановых поверхностей он рассматривает эти поверхности как однородные проводники, по которым может течь электрический ток. После этого Вейль переходит к определённой критике Клейна как математика предшествующего периода; эта критическая часть его речи содержит дорогие для автора мысли об отношении «чистой» и «прикладной» математики и о месте математики в мировой культуре:
«Всё, обретающее форму, пребывает в непреодолимом напряжении; с одной стороны., оно стремится к некому идеалу, олицетворяющему объективную реальность, требования практической жизни и потому нечто необходимое, как будто устами человека говорит неведомая сила, находящаяся вне его; с другой стороны, всё, что обрело форму, принадлежит истории духовной культуры и неотделимо от исторического процесса — оно не остаётся в нём лишь мёртвым грузом, а продолжает влиять на этот процесс. Так и наука — это учение о законах природы, высшая объективная ценность, которой человек покорно служит, и в то же время это область человеческой деятельности, суверенная сама по себе, независимо от своих плодов; подобно богу она пребывает в состоянии вечной завершённости и вечного становления. В математике особенно велика опасность ограничиться лишь первой, практической стороной дела, связанной с объективной реальностью, ибо математики склонны к абсолютизации. Клейну эта односторонность не была свойственна. Лекции, которые он читал во время войны об истории математики
XIX века4, свидетельствуют о его глубоком понимании духа истории: он никогда не отрывал факты от их исторического фона. Этим объясняется и его сдержанное отношение к основаниям5, хоть он и охотно подчёркивал, что процесс незнания начинается, так сказать, с середины и далее развивается не только по восходящей, но и по нисходящей линии, теряясь в неизвестности. Однако наша задача заключается в том, чтобы постараться в обоих направлениях пробиться сквозь туман неведомого, но, конечно, представление о том, что колоссальный слон науки, несущий на себе груз истины, стоит накаком-то абсолютном фундаменте, до которого человек может докопаться, является лишь легендой. 10Ещё и в другом отношении деятельность Клейна представляется мне имеющей недостаточный размах. Он смотрел на всё непредвзято и всячески способствовал сближению математики с естественнонаучной и технической сторонами её приложений. Но следует иметь в виду, что помимо этого математика играет весьма существенную роль в формировании нашего духовного облика. Занятие математикой — подобно мифотворчеству, литературе или музыке — это одна из наиболее присущих человеку областей его творческой деятельности, в которой проявляется его человеческая сущность, стремление к интеллектуальной сфере жизни, являющейся одним из проявлений мировой гармонии. Клейн сетовал, что «в немецком обществе ещё, видимо, не сформировалась единая культура, включающая точные науки как одну из обязательных компонент». Если ныне в этом отношении наметился некоторый перелом, то это, видимо, можно объяснить возросшим интересом к технике, благодаря чему широкие массы приобщаются к культуре точного знания, хотя мой личный опыт общения с подрастающим поколением не всегда это подтверждал: я неоднократно замечал, что, скажем, увлекающиеся автомобильным спортом молодые люди зачастую довольно враждебно относятся к теории и отнюдь не склонны к серьёзному изучению механики. Во всяком случае мне представляется очень важным то обстоятельство, что в нашем обществе вновь ожил тот вид интеллектуального, или — употреблю здесь слово, которое многие считают скомпрометированным, — метафизического мышления, о котором я говорил выше. Это связано с изменившимся отношением к достоянию культуры, о котором свидетельствует не безупречная, но вдохновенная книга Шпенглера или гораздо более основательная «Философия символических форм» Кассирера; мощный толчок в этом направлении дала и теория относительности. Весьма симптоматичен также тот интерес, который привлекают ныне вопросы античной математики, о чём свидетельствуют такие книги, как «Платон и пифагорейцы» Эриха Франка или «Отрывки из математической классики» Шпейэера, а также такие явления, как деятельность рано ушедшего от нас Грёзера, которому мы обязаны реконструкцией «Искусства фуги» Баха. Эта сторона дела была по природе несколько более чужда Клейну, чем вопросы приложений математики. Несмотря на всю глубину его философских высказываний, выражавших опыт человека редкой разносторонности и творческой силы, он никогда не стремился проникнуть до конца в смысл основных философских проблем: здесь Клейн оставался верен догмам своего времени, эмпиризму и узко понимаемой психологии, крайним выразителем которых является Мах и которые ныне, даже с эмпирически непредвзятой точки зрения, представляются нам всё более и более сомнительными»6.
Эти общетеоретические расхождения между учителем и учеником никогда не мешали Вейлю по достоинству оценить место Клейна в мировой математике:
«Таким был Клейн, оставивший печать своего гения на целой эпохе, сохранивший свою мощь и значение и в настоящем, первооткрыватель новых путей в теории групп, в абстрактной алгебре и в топологии. Зажжённое им пламя не нуждается в защите унылой традиции: оно полыхает под всеми горшками, под всеми 11 яствами математической кухни и совершает малую и великую работу на пользу современности. Его творения остаются с нами и имя его не подлежит забвению»7.
Вернёмся, однако, к хронологической канве жизни и деятельности Г. Вейля. Мы уже указывали, что в 1913 г. он покинул Гёттинген и переехал в Цюрих. Можно предполагать, что причины переезда Г. Вейля в Цюрих коренились не только в соблазнах профессуры и более высокого оклада (не лишнего для молодого учёного, лишь недавно обзаведшегося семьёй), но и в том интересе, который вызывал у Г. Вейля научный и человеческий облик некоторых (во всяком случае — одного) из его будущих коллег по цюрихскому политехникуму — ведь, зная Вейля, нетрудно догадаться, что ему вовсе не претила мысль оказаться коллегой па кафедре Альберта Эйнштейна! Правда, сотрудничество Вейля и Эйнштейна продолжалось недолго, но оно принесло глубокие плоды.
Именно в эти годы А. Эйнштейн был занят разработкой основ общей теории относительности, — и этот круг идей сразу же захватил Г. Вейля. Я позволю себе высказать предположение, что поразительный по ясности и стройности набросок геометрических идей Римана, составляющий вступительную, «математическую» часть знаменитого мемуара А. Эйнштейна от 1916 г. «Основы общей теории относительности»8, несёт на себе следы бесед с таким знатоком римановой геометрии, каким был Г. Вейль. Но несравненно значительнее было влияние А. Эйнштейна на Г. Вейля! Мемуар Эйнштейна вышел в свет в 1916 г., — а уже в 1917 г. Г. Вейль читал в цюрихском политехникуме курс лекций по общей теории относительности (имевшей в то время всего год от роду!). Эти лекции составили содержание книги Вейля, вышедшей в свет летом 1918 г. под названием «Пространство, время,
Г. Вейлю никогда не приходилось жаловаться на недостаток внимания к своему творчеству, — но ни одна его книга не имела такого успеха, как «Пространство, время, 12 материя». Второе издание этой книги появилось уже в 1919 г., третье — в 1920 г., четвёртое — в 1921 г., первые английский и французский переводы — в 1922 г. (а последние — соответственно в 1952 г. и в 1958 г.), пятое издание — в 1923 г. При этом каждое издание своей книги Г. Вейль дополнял и перерабатывал, так что отличие пятого издания от первого и в объёме книги и в её содержании уже весьма и весьма значительно. Однако многое меняя в деталях, Г. Вейль не менял общего замысла своего сочинения; неизменными оставались также выразительный язык, обилие впечатляющих примеров, глубина и продуманность математических конструкций и внимание к общефилософским вопросам, выраженное уже в открывающих книгу вдохновенных гекзаметрах немецкого поэта Фридриха Гёльдерлина:
|
Aber ins Mondlicht steigen herauf die zerbrochenen Säulen Und die Tempeltore, die einst der furchtbare traf, der geheime Geist der Unruh, der in der Brust der Erd und der Menschen Zürnet und gärt, der Unbezwungene, der alte Eroberer. Der die Städte wie Lämmer zerreisst, der einst der Olympus Stürmte, der in den Bergen sich regt und Flammen herauswirft, Der die Wälder entwurzelt und durch den Ozean hinfährt, Und die Schiffe zerschlägt, und doch in der ewigen Ordnung Niemals irre dich macht, auf der Tafel deiner Gesetze Keine Silbe verwischt, der auch dein Sohn, о Natur, ist, Mit dem Geiste der Ruh aus einem Schosse geboren. Hölderlin, Die Musse.
|
|
Но в лунном сияньи вздымаются к небу колонны, порталы и стены, Снесённые некогда диким, таинственным, страшным Духом Неистовства, тем необузданным духом, Что в недрах земных и в душах людских клокочет и бродит. Древле Олимп покорявший, волком он рвёт города, Горы ворочит и пламень из них иссекает, Ломает леса, смерчем летит в океане И топит в волнах корабли; и всё ж твой извечный порядок Ему никогда не нарушить, и со скрижалей твоих Ни знака ему не стереть, ибо он сын твой, Природа, Из чрева единого с Духом Покоя рождённый. Гёльдерлин, «Часы досуга»
(Перевод В. Л. Вишняка.) |
Мы не остановимся здесь ни на философских взглядах Вейля, ни на его физических воззрениях; однако о чисто математических особенностях книги [5] хочется сказать несколько подробнее. Книга начинается с общей трактовки понятия «эвклидова пространства». При этом Вейль резко разрывает с существовавшей традицией: если ранее при аксиоматическом описании геометрии, как правило, за основу брали следующую эвклидовской схеме систему аксиом, которой учитель Вейля Давид Гильберт придал не так давно совершенно законченный вид (см. указанную на стр.8 книгу «Основания геометрии» Гильберта), то Вейль исходит из совсем другой концепции, порождённой не геометрией, а скорее 13 алгеброй. А именно, во главу угла он кладёт понятие «вектора»: в его аксиоматике геометрии основными (неопределяемыми) понятиями являются понятия «вектора» и «точки», а основными (неопределяемыми), отношениями — алгебраические операции векторной алгебры и операция откладывания вектора от точки. Сегодня уже нет, кажется, нужды доказывать высокие научные и методические достоинства этой геометрической схемы, — но значение первой попытки положить понятие вектора в основу развёрнутых геометрических конструкций трудно переоценить.
К сожалению, последние слова хорошо понятны лишь математикам, постоянно встречающим в своей практике «векторные пространства», но никогда, практически, не имеющим дело с гильбертовой аксиоматикой, но не педагогам, многие из которых до сих пор считают гильбертов путь обоснования эвклидовой геометрии если не единственным, то, во всяком случае, самым лучшим. До сих пор в курсе геометрии наших средних школ вообще отсутствовало понятие вектора, — и поэтому концепции Вейля не могли найти там никакого отражения. Но — и это ещё печальней! — также и в курсе «Оснований геометрии» наших университетов и педагогических институтов, готовящих преподавателей средней школы, идущая от Г. Вейля идея о возможности «векторного» обоснования геометрии полностью игнорировалась; поэтому выпускники пединститутов не получали никакого представления о возможности строгого построения геометрии на пути, отличном от намеченного в «Основаниях геометрии» Д. Гильберта9. Учитывая интересы этой группы читателей нашей брошюры, быть может, уместно остановиться на схеме Вейля несколько подробнее10.
В основу своего понимания термина «эвклидово пространство» Г. Вейль кладёт объекты двух родов: «векторы» и «точки». Связь между 14 векторами и точками определяется тем, что каждым двум точкам
A и B отвечает единственныйвектор AB, а каждымточке A ивектору a — единственнаяточка B — такая, чтоAB = a. Последняя аксиома Вейля, касающаяся связи точек и векторов, может быть записана в виде следующего равенства, выполняющегося при любых точкахA, B и C: AB + BC = AC.
Далее для векторов определены операции сложения и умножения вектора на число, удовлетворяющее всем обычным свойствам: так, например, всегда
a+b=b+a иα(βa) = (αβ)a. После этого«прямая» AB определяется как совокупность всех такихточек M, чтоOM = OA + λAB,
где точки O, A и B фиксированы, λ — произвольное число (рис.2); «плоскость» ABC определяется как совокупность всех таких
точек M, чтоOM = OA + λAB + μAC,
где точки O, A, B и C фиксированы, а числа λ и μ произвольны.
Рис. 2.Наряду с этим множество векторов должно удовлетворять «аксиоме размерности»: каждые четыре вектора должны быть линейно зависимы, но три линейно независимых вектора должны существовать. Наконец, в множестве векторов должно быть определено «скалярное умножение», coпocтaвляющее любым двум векторам
a и b число ab, удовлетворяющее условиям
- коммутативности:
ab = ba для любыхвекторов a, b; - линейности:
(λ1a1 + λ2a2)b = λ1a1b + λ2a2b для любых векторовa1, a2, b и любыхчисел λ1, λ2; - положительной определённости:
aa = a2 > 0 приa ≠ 0, где 0 — «нуль-вектор», прибавление которого не меняет никакого вектора, иa2 = 0 приa = 0. Огромным достоинством этой общей схемы является широкая возможность её обобщения. Во-первых, можно полностью отказаться от понятия скалярного произведения, — и при этом мы придём к иной геометрической схеме, описывающей «аффинное пространство». (В книге [5] Вейль определяет сначала понятие «аффинного пространства» и лишь затем — понятие «эвклидова пространства»). Далее, можно, изменив соответствующим образом «аксиому размерности», определить (аффинное или эвклидово!) пространство любого числа измерений — бесценная возможность для теории относительности, оперирующей главным образом с четырёхмерным пространственно-временным континуумом. Наконец, можно, отказавшись от аксиомы положительной определённости скалярного произведения, перейти от «эвклидова пространства» к «псевдоэвклидову пространству» («пространству Минковского»), столь важному для геометрической трактовки идей теории относительности.
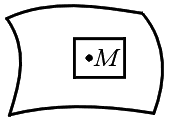
Рис. 3.
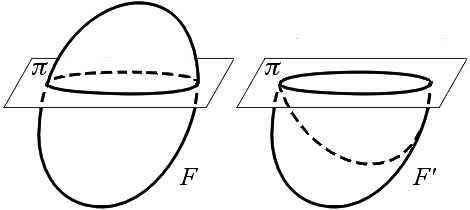
Но сравнительно простая схема эвклидова11 пространства может быть использована лишь в «специальной» теории относительности, — «общая» же теория относительности требует большего. А. Эйнштейн при построении теории относительности существенно опирался на общие построения Б. Римана, изложенные в его речи «О гипотезах, лежащих в 15 основании геометрии»12, приобретшей широкую известность благодаря глубоким комментариям Г. Вейля [1]. (В конце своей речи Риман с гениальной прозорливостью предсказал значение развитых им конструкций для физики.) Сущность идей Римана заключается в следующем. Хорошо известно, что каждая поверхность в трёхмерном пространстве «в малом» (т.е. в окрестности каждой своей точки M) «устроена» как обычная (эвклидова) плоскость: её «геометрия» мало отличается от «геометрии» плоскости, касательной к поверхности в
В книге [5] Г. Вейль развил эту концепцию дальше. Движимый желанием сделать реальный четырёхмерный (пространственно-временной) «мир» возможно более гибким, он предложил конструировать «искривлённые» пространства из (многомерных) «плоских площадок», устроенных не как обычное пространство Эвклида, а как «аффинное пространство», лишённое всякой метрики. Такие пространства (чисто математической их теории посвящена статья [14], вышедшая в свет почти одновременно с книгой [5]) Г. Вейль назвал «пространствами аффинной связности»; их важный частный случай, подробно разобранный в книге [5], навсегда сохранил название «пространств Вейля».
Согласно схеме Клейна, о которой уже говорилось выше, каждое пространство характеризуется своей «группой автоморфизмов» — совокупностью преобразований, сохраняющих рассматриваемые в этой геометрии свойства фигур. Для эвклидовой геометрии роль таких «автоморфизмов» играют движения, а для аффинной геометрии — так называемые аффинные преобразования, характеризующиеся тем, что они переводят прямые линии в прямые линии; примерами аффинных преобразований могут служить, например, так называемый «сдвиг» (рис.4а) или «сжатие к прямой» (рис.4б). Так как преобразования такого рода не сохраняют ни расстояний между точками, ни величин углов, то в аффинной геометрии (а следовательно — и в «геометрии аффинной связности») нельзя говорить ни о расстояниях, ни об углах. 16 Однако величина отношения двух заданных на одной прямой отрезков не меняется при аффинных преобразованиях; соответственно этому и в «пространстве аффинной связности» Вейля можно говорить о величине отношения двух «отрезков» (двух дуг) одной «геодезической линии» — «линии нулевой искривлённости» пространства аффинной связности, играющей в этом пространстве роль прямой.
![]()
/_ AOA' = α = const 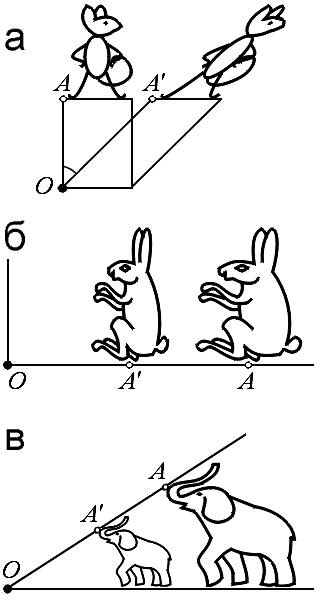
![]()
OA' OA
= k = const ![]()
OA' OA
= k = const Рис. 4.
Существует ещё одна крайне важная группа преобразований, «промежуточная» между движениями и аффинными преобразованиями, — это группа преобразований подобия, сохраняющих форму всех фигур, но меняющих их размеры (рис.4в). В геометрии, «автоморфизмами» которой служат преобразования подобия, имеет смысл понятие угла между линиями, но понятие расстояния лишено смысла (ибо преобразования подобия сохраняют углы, но не расстояния!). «Пространства Вейля» как раз и характеризуются тем, что локально они устроены как плоское пространство, автоморфизмами которого являются преобразования подобия; в этих (искривлённых) пространствах также нельзя говорить о расстояниях, но имеет смысл понятие угла между линиями.
Заметим, что впоследствии Г. Вейль [15] пошёл ещё дальше, рассмотрев «искривлённые» пространства, в малом устроенные как плоские «площадки», группа автоморфизмов которых задаётся проективными преобразованиями или конформными преобразованиями (инверсиями). Эти построения Вейля были затем глубоко развиты и усовершенствованы знаменитым французским математиком Эли Картаном, научное творчество которого так тесно связано с творчеством Вейля, как это редко бывает у двух разных учёных (см., например, книгу: Э. Картан. Пространства аффинной проективной и конформной связности. Казань, 1962).
Книга [5] является классическим произведением и физической и геометрической литературы, и не удивительно, что вскоре (в 1925 г.) она была награждена одной из самых почётных из имевшихся тогда международных математических премий: премией имени Н. И. Лобачевского, присуждавшейся в те годы Казанским физико-математическим обществом за выдающиеся работы в области геометрии.
Удивительна продуктивность Г. Вейля в его первые цюрихские годы! За период с 1913 по 1923 г. он опубликовал
Иной характер имеет книга «Математический анализ проблемы пространства» [17], излагающая содержание лекций, прочитанных Г. Вейлем весной 1922 г. в Барселоне и в Мадриде.
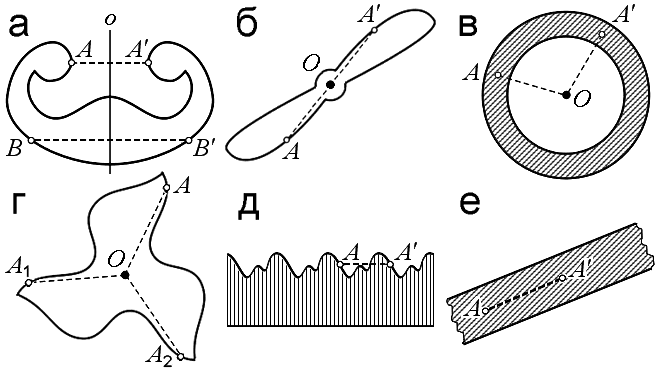
Здесь хочется остановиться на связи установок Г. Гельмгольца с идеей симметрии. В настоящее время «симметричность» фигуры характеризуют обычно, указывая группу «автоморфизмов» или «симметрий», переводящих фигуру в себя. Так, изображённая на рис.5а фигура обладает «осевой симметрией», поскольку она переводится в себя симметрией относительно вертикальной
Ряд работ Вейля 1913–1923 гг. продолжает тематику, начатую в его исследованиях гёттингенского периода: они посвящены «граничным задачам» теории дифференциальных уравнений, вопросам распространения электромагнитных волн (см., например, работу [19]), вопросам, относимым сегодня к функциональному анализу. Наряду с этим в его творчестве возникают новые большие направления; Очень много работ было посвящено кругу вопросов, связанных с книгами [5], [16] и [17], — общей теории относительности Эйнштейна (см., например, [20]), дифференциальной геометрии обобщённых пространств [21], общим концепциям «геометрического пространства» [22]. Несколько исследований было посвящено вопросам статистической физики (см., например, [23]), другие относились к области топологии [24]. В 1923 г. на испанском языке была опубликована статья «Введение в комбинаторный анализ» [25], которая первоначально не привлекла особого внимания, поскольку в то время проблемы комбинаторики казались навсегда ушедшими с магистральной линии развития математики. Однако в 1951 г. (через 28 лет после появления работы [25]!) американские математики сочли уместным перевести её на английский язык, — и это неожиданное внимание к старой работе Вейля было связано с обстоятельствами, о которых стоит сказать подробнее.
В 20-х и 30-х годах нашего столетия увлечение теоретико-множественными конструкциями, связанными с развитым аналитическим аппаратом теории функций действительного переменного и теории функций комплексного переменного, достигло, пожалуй, своего апогея. Понятие непрерывности представлялось самым важным во всей математике — именно в эти годы знаменитый французский математик Анри Лебег писал, что «если все законченные точные вычисления (т.е. не связанные с непрерывными функциями и бесконечными процессами.
Наряду с этим необходимо отметить цикл исследований по «геометрии в целом», начавшийся со знаменитой
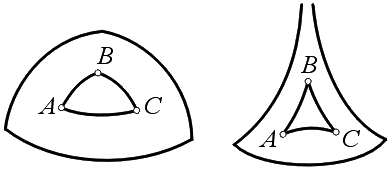
Нетрудно заметить, что сумма углов треугольника ABC, образованного «кратчайшими соединениями» трёх точек
В том же 1916 г., когда была опубликована эта работа [2], вышла в свет и большая
| ∑ | e2πif (n) = | ∑ | cos [2πf (n)] + i | ∑ | sin [2πf (n)], |
| n | n | n |
где
| N–1 | N–1 | N–1 | ||||||||
| S = | ∑ | e2πi·an/N = | ∑ | cos | 2πan N |
+ i | ∑ | sin | 2πan N |
, |
| n=0 | n=0 | n=1 | ||||||||
где N и a — целые числа. Ясно, что если a делится на N, то каждое слагаемое
| = | e2πia – 1 e2πi·a/N – 1 |
= | 1 – 1 e2πi·a/N – 1 |
= 0. |
Таким образом, имеем
| S = | ì | 0, если a не делится на N, |
| í | ||
| î | N, если a делится на N, |
откуда уже видна связь суммы S с теоретико-числовыми характеристиками числа a.
Разумеется, «сумма Вейля» S является весьма несложной; в общем же случае мы, как правило, не сможем вычислить точное значение подобной суммы. Однако Вейль указал методы, позволяющие приближённо оценивать любые суммы такого вида, и сумел извлечь из этих оценок ряд новых теоретико-числовых фактов. С использованием идей его
Наконец, в 1918 г. (одновременно с книгой «Пространство, время, материя») вышла в свет небольшая книга Г. Вейля «Континуум» [30], знаменующая ещё одно важное направление творчества этого замечательного математика. Для Вейля всегда был характерен глубокий интерес к вопросам обоснования математики, к философии науки и к 24 проблемам математической логики. После того, как теория вещественного числа получила в конце
Новое большое направление математического творчества, на долгие годы ставшее для Г. Вейля основным, было начато рядом публикаций 1924 г. Я говорю здесь о теории представлений групп преобразований (и о теории инвариантов этих групп), а также о физических приложениях этих теорий.
В чисто математической теории представлений групп Г. Вейлю бесспорно принадлежит одно из самых первых 25 мест: достаточно упомянуть здесь классическую теорему, Петера–Вейля (см. переведённую и на русский язык работу [34]), составляющую математический фундамент чуть ли не всех дальнейших построений, или замечательную работу в четырёх частях [35], опубликованную Вейлем в 1925–1926 гг. (эта статья также частично переведена на русский язык). Однако ещё больший интерес для нас представляют физические применений этой теории, на которых следует остановиться подробнее.
Физический аспект теории представлений групп состоит в учёте и использовании соображений симметрии, связанных с различными физическими процессами. Такие соображения симметрии возникают в физике двояким образом.
Для того чтобы проиллюстрировать сказанное, достаточно указать на один простейший пример. Единственным выражением, связывающим координаты
ax, ay, az произвольноговектора a и не меняющим своего значения при любом повороте осей системы координат, является сумма D квадратов координат вектора:D = ax2 + ay2 + az2,
равная квадрату длины вектора a (и любая функция выражения D), но хорошо известно, что закон преобразования частных производных
∂/∂x, ∂/∂y, ∂/∂z некоторой функцииf (x, y, z) при повороте осей системы координат совпадает с законом преобразования координат вектора, причём вторые производные∂2/∂x2, ∂2/∂y2, ∂2/∂z2 преобразуются как 26 квадраты координат! Это обстоятельство определяет роль в физике так называемого «оператора Лапласа»
Δ = ∂2 ∂x2
+ ∂2 ∂y2
+ ∂2 ∂z2
— простейшие физические законы, удовлетворяющие накладываемым изотропностью и однородностью пространства «условиям симметрии», могут записываться лишь одним из следующих трёх дифференциальных уравнений (здесь
u = u(x, y, z, t) —какая-то функция, имеющая инвариантный физический смысл;f = f (x, y, z, t), a = a(x, y, z, t) — известные функции):
Δu = f («уравнение Пуассона», при f = 0
обращающееся в «уравнение Лапласа»);Δu = a ∂u ∂t
(«уравнение теплопроводности»); Δu = a ∂2u ∂t2
(«волновое уравнение»).
(Заметим, что требованиям инвариантности относительно «преобразований Лоренца» удовлетворяет одно только «волновое уравнение», где дополнительно должно быть а = const).
Развитая теория представлений групп необходима для физики потому, что интересующие нас физические объекты могут быть довольно сложной природы, например могут иметь много компонент, образовывая, так сказать, «многомерный вектор», — и при этом любые такие объекты должны удовлетворять «условиям симметрии», определяющимся «симметрией» обычного трёхмерного пространства или четырёхмерного пространственно-временного континуума.
В настоящее время широкое использование «соображений симметрии» в физике является довольно обычным. По этому поводу читателю можно порекомендовать, например, книгу Л. Д. Ландау и Е. М. Лифшиц. Механика. М., Физматгиз, 1958 (см., в частности, §3 этой книги). Укажем также, что в одном из лучших современных курсов классической (нерелятивистской!) квантовой механики — в книге Л. Д. Ландау и Е. М. Лифшиц. Квантовая механика. М., Наука, 1965 — выводу следствий из соображений симметрии посвящено около трети общего числа страниц; в релятивистской же (т.е. базирующейся на теории относительности Эйнштейна) квантовой механике эти соображения играют ещё большую роль, чем в классической квантовой механике. (По поводу современной трактовки роли соображений симметрии в физике см. также Ю. Вигнер. Симметрия и законы сохранения. Успехи физических наук, т. 83, вып. 4, 1964,
Но так обстоит дело сегодня! В десятых же и двадцатых годах всё было по-другому; так, например, ещё в начале нашего столетия известный физик и астрофизик Дж. Джинс (автор некогда широко популярной космогонической гипотезы) активно протестовал против включения в курс физического факультета Принстонского университета элементов теории групп, утверждая, что
Здесь уместно коснуться дальнейшей судьбы главного «научного детища». Г. Вейля, каким бесспорно является теория представлений групп и физические приложения этой теории. Во времена Вейля роль соображений симметрии в физике была несравнима с той, какую они играют в наши дни.
Мы здесь намеренно ограничиваемся изложением положения дел в том виде, каким оно представлялось в конце 29
Значение идущих от Г. Вейля соображений симметрии для физики можно проиллюстрировать некоторыми из наиболее впечатляющих открытий последнего времени. Согласно современным квантовомеханическим представлениям, семейства элементарных частиц отвечают «собственным векторам» некоторого оператора Шрёдингера; при этом обычно соответствующий оператор Шрёдингера удовлетворяет (хотя бы приближённо) довольно жёстким условиям симметрии, из которых вытекают определённые соотношения между свойствами отвечающих этому оператору элементарных частиц. Так, например, симметрия оператора Шрёдингера относительно группы O3 вращений трёхмерного пространства согласована с наличием тройки линейно независимых векторов, которым должна отвечать тройка элементарных частиц с близкими свойствами; знание структуры группы O3 позволяет математически описывать свойства этой тройки частиц. Такое описание было дано на основе отвечающего группе O3 «принципа симметрии» английским физиком Н. Кеммером ещё в 1938 г. — а первая из тройки элементарных частиц, полностью удовлетворяющих предсказанным Кеммером свойствам («пионов» или
«пи-мезонов»), была открыта англичанином С. Пауэлом лишь в 1947 г. — через девять лет после появления работы Кеммера. Существенно при этом, что оператор Шрёдингера для пионов оказался зависящим от некоторой совершенно новой величины («изотопического спина»), которую можно рассматривать как вектор в некотором трёхмерном пространстве (не имеющем никакого отношения к реальному трёхмерному пространству, в котором мы живём и в котором наблюдаются элементарные частицы!), и инвариантным относительно вращений в пространстве этого вектора. Характер этого вспомогательного «пространства» нам совершенно не важен, ибо для применений соображений симметрии важно лишь знание группы автоморфизмов, не меняющих вид оператора Шрёдингера.Последнее обстоятельство сыграло громадную роль в дальнейшем развитии теории элементарных частиц. Мощное развитие экспериментальной техники в последние годы, в частности появление гигантских ускорителей, привело к тому, что новые элементарные частицы стали открываться десятками — и учёные буквально растерялись от этого свалившегося на них непрошенного богатства, которым они не умели распорядиться, в котором даже разобраться казалось немыслимым. Поэтому с таким энтузиазмом было встречено открытие американского физика
М. Гелл-Манна и израильского учёного И. Неемана, которые независимо друг от друга заметили, что существует целый ряд семейств из восьми элементарных частиц с близкими свойствами, совпадающими с теми, которые должны были бы получиться в случае использования оператора Шрёдингера, обладающего симметрией, определяемой родственной O3 группой SU3 («группа унитарных преобразований комплексного трёхмерного пространства»), хорошо действующей в восьмимерном пространстве. 30 Это глубокое замечание сразу позволило «навести порядок» в новом хозяйстве — частицы естественно распадались на классы из восьми «родственников» (знаменитый «восьмиричный путь» современной теории элементарных частиц!). При этом замечательно, что вид оператора Шрёдингера (т.е. динамических уравнений) для новых элементарных частиц и даже то, от каких величин этот оператор зависит и в каком пространстве действует, пока совершенно неизвестны (и даже неясно, как можно подступиться к решению соответствующих вопросов); «восьмиричный путь» указывает лишь, что этот неизвестный оператор в неизвестном пространстве обладает определённой симметрией, — и это уже даёт очень много для изучения элементарных частиц и даже для предсказания их свойств.В 1961 г. М. Гелл-Манн присутствовал на конференции по физике элементарных частиц, на которой было объявлено об открытии ещё одной частицы со свойствами, близкими к свойствам восьми уже известных частиц, не укладывающихся в схему «восьмиричного пути».
Гелл-Манн сразу же заметил, что теперь частиц уже стало девять и что если бы добавить к ним ещё одну, то получится семейство из десяти частиц, полностью соответствующее десятимерному пространству, в котором тоже может действовать группа SU3. Тут же он объявил, что должна существовать эта «десятая» частица — «омега-минус барион», обладающая строго определёнными свойствами. И в действительности в феврале 1964 г. американские экспериментаторы У. Фаулер и Н. Сеймиос, исходившие из предсказанийМ. Гелл-Манна, открыли элементарную частицу, свойства которой в точности совпали с описаннымиГелл-Манном свойствами «омега-минус бариона»23!Но ведь группа SU3 — это группа преобразований трёхмерного пространства; следовательно, она может действовать и в трёхмерном, пространстве.
М. Гелл-Манн смело указывает, что трём векторам такого трёхмерного пространства должны отвечать три частицы с совсем уже фантастическими свойствами: так, например, заряд этих частиц должен равняться 1/3 заряда электрона (который всегда считался наименьшим из возможных зарядов!). Гипотеза о таких частицах была выдвинутаМ. Гелл-Манном в одной из его публикаций 1964 г.; одновременно аналогичную гипотезу выдвинул и другой американский физик Г. Цвейг (см. по этому поводу обзоры, указанные в первом подстрочном примечании на стр.32). Никто никогда не видел этих частиц, но если они существуют, то они должны быть «самыми элементарными» из всех основных частиц (так как трёхмерное пространство — простейшее из всех, в которых может действовать группа SU3, и все остальные пространства можно, в определённом смысле, построить из вектора трёхмерного пространства).Итак, новые частицы были «придуманы» (здесь, разумеется, это слово является более подходящим, чем слово «открыты») — оставалось только их назвать (и ещё, пожалуй, найти). Какое же название можно предложить для частиц со столь удивительными свойствами? В самом непонятном из романов знаменитого ирландского писателя Джеймса Джойса,
вообще-то не отличающихся особенной простотой (название этого романапо-русски обычно передаётся словами «Поминки по Финнегану», хотя никто не может быть уверен, что именно этот смысл вкладывал автор в английское название «Finnegan's Wake»), в полубредовой сцене пиракакой-то голос произносит: «Три кварка для мистера Кларка». Это выражение понравилосьГелл-Манну: разумеется, «три кварка», про которые у Джойса говорит неизвестно кто и неизвестно почему, — это и есть загадочные частицы. И вот уже целый ряд лет 31 физики-экспериментаторы безуспешно ищут загадочные «кварки» на своих ускорителях, а астрономы и астрофизики строят увлекательные теории о роли этих частиц в прошлом и будущем, — а меж тем по сегодняшний день упрямые частицы упорно не даются учёным, и уж никто, кажется, не в состоянии сказать, существуют ли «кварки» где-нибудь во Вселенной или нет24.Укажем ещё, что в 1929 г. Г. Вейль [36], развивая те же идеи о «симметрии» элементарных частиц, которым была посвящена его книга [6], рассмотрел гипотетический случай «простейшей» частицы нулевой массы; он указал, что такая частица может существовать в одной из двух форм, каждая из которых является зеркальным отражением другой. Поскольку в то время физики не знали частиц, к которым можно было применить теорию Вейля, статья [36] имела характер чисто умозрительный и особого внимания в то время не привлекла; к тому же гипотетические частицы Вейля изменяли свой характер при отражении от плоскости, на основании чего знаменитый швейцарский физик-теоретик В. Паули объявил в 1933 г. их несуществующими25. Однако в 1956 г. (через год после смерти Г. Вейля!) Ли и Янг установили, что частицы, меняющие свои свойства при отражении от плоскости, нельзя считать противоречащими физическим законам; с другой стороны, в том же 1956 г. американские экспериментаторы Ф. Рейнес и К. Коуэн доказали существование новой частицы «нейтрино», теоретически предсказанной В. Паули ещё в 1931 г.: эта частица не обладает ни массой, ни электрическим зарядом (но имеет «спин», который можно условно представлять себе как характеристику вращательного движения частицы) и полностью подходит под разработанную Вейлем схему. В этой связи физики разных стран — Л. Д. Ландау в Москве (снова Ландау!), Ц. Ли и Ч. Янг в
Нью-Йорке (снова Ли и Янг!), а также индус А. Салам и знаменитые американцы Р. Фейман иМ. Гелл-Манн, вспомнили про работу [36] Вейля; они объявили, что наряду с нейтрино должно существовать и «антинейтрино», получающееся из нейтрино отражением от плоскости. И действительно, сегодня мы имеем уже и экспериментальные подтверждения существования «антинейтрино», теоретически предсказанного Вейлем ещё в 1929 г.!26Наконец отметим, что даже и весьма общие построения Вейля в настоящее время оказались во многом недостаточными для нужд теоретической физики. Это обстоятельство вызвало к жизни большой цикл исследований выдающегося московского математика И. М. Гельфанда и его учеников и сотрудников, в которых рассматривается, как могут действовать «группы симметрии» тех или иных физических объектов в бесконечномерном пространстве Гильберта (ср. выше, стр.7)27, причём и полученные в этом направлении результаты были сразу же подхвачены физиками. 32
Продолжим, однако, хронологический обзор жизни и деятельности Г. Вейля. Во второй половине
Проживая в Цюрихе, Г. Вейль сохранял связи и с родным ему университетом в Гёттингене; так, например, он охотно печатался в старинных «Известиях Гёттингенского научного общества» (Nachrichten der Gesellschaft der Wissenschaft zu Göttingen), которые весь учёный мир называл просто «Гёттингенскими известиями» (Göttinger Nachrichten). В 1923 г. Вейль по приглашению Ф. Клейна ненадолго приезжал в Гёттинген для чтения курса лекций; эта поездка принесла ему много удовлетворения. К сожалению, следующий приезд Г. Вейля в Гёттинген оказался гораздо менее удачным.
В 1930 г. Д. Гильберту было предложено покинуть маленький провинциальный Гёттинген и перебраться в Берлин; он согласился на это при условии, что возглавляемая им кафедра в Гёттингене (которой некогда руководил К. Ф. Гаусс!) будет передана Вейлю. Кандидатура Вейля на замещение кафедры Гаусса для всех математиков казалась 33 весьма естественной; однако жизнь Германии определяли в те годы не математики. Начало
Приход фашистов к власти ознаменовался массовым увольнением из Гёттингенского университета учёных еврейской национальности; вместе с евреями покинул Гёттинген и немец Г. Вейль. Он перебрался в маленький американский городок Принстон, знаменитый своим Институтом высших исследований (Institute for Advanced Study) — замечательным физико-математическим научно-исследовательским институтом, в котором нашли приют также Альберт Эйнштейн и Юджин Вигнер, выдающийся физик, независимо от Вейля пришедший к мысли о возможности использования в физике идей симметрии и посвятивший всю свою жизнь разработке этих идей29. Для Вейля, влюблённого в немецкую культуру и в немецкую речь, переезд в Америку был не лёгким делом, — но наученный тремя годами жизни в Гёттингене, он, видимо, предпочитал иметь между собой и Гитлером океан. 34
Последующие годы в жизни Вейля были довольно спокойными. Он жил в Принстоне, пользуясь всеобщим уважением и продолжая разрабатывать все научные направления, начатые в предшествующих работах. Так, например, в 1935 г. в «Американском математическом журнале» была напечатана его совместная с Р. Брауэром статья «Спиноры в
 | |||||||
| |||||||
| Рис. 8. |
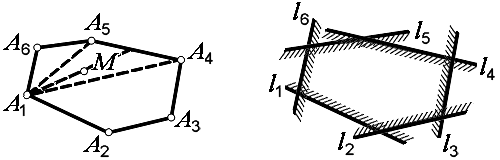
К 1935 г. относится как будто неожиданная для Вейля небольшая заметка со скромным названием «Элементарная теория выпуклого многогранника» [43]. Эта заметка излагает соображения, которые Г. Вейль развивал на последнем руководимом им в Гёттингенском университете семинаре по теории выпуклых тел летом 1933 г. — в это неспокойное время Г. Вейль находил некоторый отдых от политических забот, разбирая со студентами вопросы, относящиеся, по существу, к элементарной геометрии. Содержание этой заметки достаточно просто. Выпуклый многоугольник на плоскости (рис.8, слева) можно определить как выпуклую оболочку множества своих вершин (аналитически — как множество таких
где r1, r2, …, rn — радиусы-векторы вершин
где
В 1935 г. линейные неравенства не вызывали серьёзного интереса; внимание математика такого масштаба, как Г. Вейль, к связанным с ними элементарно-геометрическим вопросам (теория выпуклых многогранников) могло даже показаться чудачеством. Однако когда в 1950 г. американские математики Г. У. Кун и А. У. Таккер напечатали в издательстве Принстонского университета привлёкший сразу же большое внимание том исследований по недавно созданной и весьма важной для приложений (а в силу этого, — и весьма модной) «теории игр», они начали этот том с переведённой Г. У. Куном старой заметки [43] Вейля30. (Надо заметить, что работа [43] была не единственной статьёй Г. Вейля 36 в данном томе «Исследований по теории игр» — см. статью [44] Г. Вейля).
В 1939 г. вышла в свет одна из замечательнейших книг Г. Вейля — его «Классические группы» [45], в которой он подытожил свои многолетние занятия теорией инвариантов и представлений групп. Немец Вейль написал эту книгу
| „Was dies heissen will, weiss jeder, Der im Traum pferdlos geritten“ |
| («Что это значит — каждый знает, кто во сне верхом скакал без коня»), |
— хотелось бы мне сказать вместе с Готфридом Келлером. Никто более меня не почувствует связанной с этим утраты силы, лёгкости и ясности выражения». Однако эти сожаления Вейля представляются не совсем основательными: и по содержанию, и по языку «Классические группы» — истинно «вейлевская» книга, соединяющая высокие научные и методические достоинства с выразительностью и даже художественностью языка, о котором можно судить хотя бы по следующему отрывку из предисловия, объясняющему основные установки автора (цитируется по русскому переводу Д. А. Райкова):
«Строгая точность, достижимая математическим мышлением, привела многих авторов к манере изложения, которая должна произвести на читателя такое впечатление, как если бы он был заключён в ярко освещённую камеру, где каждая деталь выделяется с одинаково ослепляющей ясностью, но без рельефности. Я предпочитаю открытый ландшафт под ясным небом с его глубиной перспективы, где обилие отчётливо очерченных близких деталей постепенно сходит на нет по мере удаления к горизонту. В частности, горный массив топологии лежит для этой книги и её читателя у горизонта, и поэтому те его части, которые следовало поместить в картину, даны лишь в грубых чертах. От читателя ожидается здесь готовность переключаться на точки зрения, отличные от принятых в алгебраических частях, и добрая воля к сотрудничеству.
Книга предназначена, главным образом, для тех, кто скромно пожелает узнать изложенные в ней новые вещи, а не для гордых учёных, уже знакомых с предметом...».
В 1938/39 учебном году Г. Вейль читал в Принстоне курс лекций по алгебраической теории чисел; эти лекции составили содержание его книги «Алгебраическая теория чисел» [3]. В 1943 г. вышла в свет книга Г. Вейля «Мероморфные функции и аналитические кривые» [46], написанная в сотрудничестве с сыном Иоахимом Вейлем; она появилась ровно через 30 лет после первой книги Вейля [12], также посвящённой теории функций комплексного переменного. Я не могу 37 удержаться от соблазна процитировать здесь предисловие и к этой книге, достаточно характерное для стиля Вейля:
«Пять лет тому назад мой сын Иоахим и я обнаружили в первобытном лесу математики побег, который мы назвали Мероморфной Кривой (Annals of Mathematics, 1938). Мы принесли его домой; он выглядел здоровым и привлекательным, однако, мы не знали, как с ним надо обращаться. Позже, появился садовник с Севера, искусный работник с большим опытом, Л. Альфорс31 было его имя; он знал, как надо ухаживать за нашим ростком, и под его наблюдением растение быстро обратилось в прекрасное дерево (Acta Society Sciences Fennicae, 1941). Усвоив этот урок, мы со своей стороны решили осуществить одну идею, которую раньше представляли себе довольно смутно (Annals of Mathematics, 1941, Proceedings of National Academy of Sciences, 1942), а именно, пересадить дерево Мероморф с
z-плоскости в горную местность произвольной римановой поверхности (я любил этот ландшафт с далёких дней моей юности). Эксперимент оказался удачным: на дереве стали видны почки, появились листья, однако, только будущее сможет показать нам, какие плоды принесёт наше дерево. Тем временем грозная буря войны разлучила нас с нашим мудрым садовником»32.
Работа над книгами перемежалась с работой над новыми оригинальными статьями: так, в 1945 г. вышла в свет очень важная статья алгебраического содержания [47]; в 1949 г. была опубликована глубокая статья [48], посвящённая разрабатываемым Г. Вейлем так много лет физическим применениям принципа симметрии. В 1951 г. Г. Вейль в большой статье [49] «подвёл итоги» математического полустолетия — трудно было бы указать автора, который имел бы больше прав на подобное выступление и смог бы осуществить его с большим успехом.
В том же году Г. Вейль выступил в Принстоне перед широкой аудиторией с четырьмя публичными лекциями, посвящёнными проблеме симметрии; эти лекции, которые сам Вейль называл своей «лебединой песней» в Принстоне, составили содержание книги «Симметрия» [18], опубликованной издательством Принстонского университета в 1952 г. Замечательная книга [18] ныне переведена и на русский язык (перевод Б. В. Бирюкова и Ю. А. Данилова); поэтому вряд ли уместно подробно представлять её читателю. Однако я не могу удержаться от желания процитировать слова, какими сам Вейль характеризует основную идею книги:
«Эти лекции построены следующим образом. Сначала мы несколько более подробно рассмотрим зеркальную симметрию и её роль в искусстве, в живой и неживой природе. Затем мы постепенно обобщим это понятие... при этом вначале мы будем оставаться в рамках геометрии, но затем выйдем за её пределы и с 38 помощью процесса математической абстракции вступим на путь, который в конце концов приведёт нас к математическому понятию огромной общности, к платоновской идее, стоящей за всеми частными проявлениями и приложениями симметрии. Описанная схема в известной степени характерна для всего теоретического познания: мы начинаем с некоторого общего, но туманного принципа (симметрия в первом смысле этого слова)33; затем находим важный частный случай, рассмотрение которого позволяет придать нашему понятию конкретный и точный смысл (зеркальная симметрия); далее, отправляясь от этого частного случая, мы постепенно вновь поднимаемся к общему, причём руководствуемся уже не философскими призраками, а опираемся на математическое построение и математическую абстракцию, и, если это нам удаётся, мы в конце концов доходим до понятия, носящего не менее общий характер, чем то, с которого мы начали. Может оказаться, что при этом мы потеряем значительную часть эмоциональной окраски исходного понятия, однако новое понятие будет в области мышления обладать такой же — если не большей — силой обобщения, и, кроме того, будет точным, — в отличие от первоначального туманного понятия».
«Аналитическим продолжением» книги Г. Вейля [18] является написанная под сильным влиянием «Симметрии» книга известного американского популяризатора науки Мартина Гарднера «Этот правый, левый мир», о которой мы уже упоминали выше (стр.32). В книге М. Гарднера предпринятое Г. Вейлем в начале
В 1951 г. Г. Вейль покинул Соединённые Штаты и переехал обратно в Цюрих; однако по-прежнему он наезжал в Принстон и поддерживал тесные связи с принстонскими математиками. Возвращение в любимый город, который он оставил больше 20 лет тому назад, в город его молодости и первых блестящих успехов, было радостью для Вейля ещё и потому, что он снова слышал на улицах немецкую речь, к которой был страстно привязан, — ведь и в США Вейль чувствовал себя немцем.
Однако жить Вейлю в Швейцарии оставалось уже недолго. Он ещё успел напечатать ряд интересных статей; также и его книга «Симметрия» [18] вышла в свет после возвращения Вейля в Цюрих. В Цюрихе же Вейль написал свою автобиографию, которую он назвал «Познание и сознание» (Erkenntnis und Besinnung) и в которой подробно рассказал о своих философских и общенаучных увлечениях. В 1954 г. 39 69-летний Вейль выступил на Международном математическом конгрессе в Амстердаме с приветствием от старшего поколения учёных молодым математикам (французу
В ноябре 1955 г. в Цюрихе состоялся большой банкет в ознаменование
История математики знает не много учёных, равных Г. Вейлю по своим заслугам; он принадлежит к числу классиков математической науки, о которых пишутся исследования35 и защищаются диссертации36. При этом поражает 40 разносторонность Вейля: и в арифметику (теорию чисел), и в алгебру, и в геометрию, и в анализ этот великий «математический полиглот» внёс вклад, который будут помнить многие поколения учёных. И когда сегодня мы вспоминаем Германа Вейля, то прежде всего приходит на память его колоссальная разносторонность, его умение в каждой частности видеть «математику в целом» и в «математике в целом» различать всё многообразие задач и методов, тенденций и идей — с присущей этим идеям способностью то мирно взаимодействовать, дополняя и исправляя друг друга, то яростно противоборствовать и вытеснять одна другую. При этом Вейлю всегда была глубоко чужда пристрастность в научных спорах: ко всем направлениям человеческой мысли, ко всем её достижениям и неудачам он относился с равным уважением и дружеской заинтересованностью. Судьба судила Вейлю оказаться в разных научных лагерях с двумя самыми первыми из его учителей — с Д. Гильбертом, возглавлявшееся которым формальное направление в учении об основаниях математики долгое время рассматривалось интуиционистами во главе с Л. Брауэром и Г. Вейлем как основной противник и оппонент, и с Ф. Клейном, резко отрицательно относившимся ко всей дискуссии об основаниях математики, в которой Г. Вейль был одним из главных действующих лиц. Однако это нисколько не повлияло на интерес Вейля к научным достижениям Гильберта и Клейна и на глубокое уважение, которое он питал к ним обоим (ср. выше,
Следует заметить, что Г. Вейль отнюдь не был единственным в истории науки
| 1. | Комментарий Г. Вейля к лекции Римана «О гипотезах, лежащих в основании геометрии». См. в кн.: Б. Риман. Сочинения. В немецком оригинале комментарий был приложен к осуществлённому под наблюдением Г. Вейля изданию речи Римана, вышедшей отдельной книгой в Берлине в 1918 г.; |
| 2. | Об определении замкнутой выпуклой поверхности её линейным элементом. Успехи математических наук, 3, вып. 2 (24), 1948, В немецком оригинале статья вышла в свет в 1916 г. в журнале Vierteljahrsrift der Naturforschenden Gesellschaft in Zürich, |
| 3. | Алгебраическая теория чисел. М., ИЛ, 1947. В английском оригинале книга Algebraic theory of numbers вышла в свет в 1940 г. в Принстоне (США). назад к тексту |
| 4. | Über die Gleichverteilung von Zahlen mod. Eins (О равномерном распределении чисел по модулю единица). Mathematische Annalen, 77, 1916, Перепечатано в «Избранном» (Selecta) Г. Вейля, |
| 5. | Raum, Zeit, Materie (Время, пространство, материя). Berlin, 1918. 2-е издание — Берлин, 1919 г.; |
| 6. | Теория групп и квантовая механика. М., Наука, 1986. В немецком оригинале книга Gruppentheorie und Quantenmechanik вышла в свет в 1928 г. в Лейпциге; |
| 7. | а) Zu David Hilhert siebzigsten Geburtstag Статья б) напечатана также в American Philosophical Society Year Book, 1944, |
| 8. | а) Über die Konvergenz von Reihen, die nach periodischen Funktionen fortschreiten (О сходимости рядов, разложенных по периодическим 43 функциям). Совместно с Ф. Ерошем (F. Jerosch); Mathematische Annalen, 66, 1808, |
| 9. | Singuläre Integraigleichungen mit besonderer Berücksichtigung des Fourierschen Integraltheorems (Сингулярные интегральные уравнения в связи с интегральной теоремой Фурье). Göttingen, 1908 (докторская диссертация). назад к тексту |
| 10. | a) Über die gewönliche Differentialgleichungen mit Singuleritäten und die zugehörigen Entwicklungen willkürlicher Funktionen (Об обыкновенных дифференциальных уравнениях с особенностями и об отвечающих им разложениях произвольных функций). Mathematische Annalen, 68, 1910, Статья а) перепечатана также в «Избранном» (Selecta) Г. Вейля, |
| 11. | О философии математики. М., Гостехиздат, 1934. Эта книга составлена из отрывков из вышедшей в свет в 1926 г. книги [26] Г. Вейля и из двух его статей: «Современное состояние проблемы познания в математике» (немецкий оригинал статьи был напечатан в философском журнале Symposion в 1926 г.) и «О новом кризисе основ математики» (немецкий оригинал был опубликован в математическом журнале Mathematische Zeitschrift в 1921 г. и перепечатан в «Избранном» Г. Вейля). назад к тексту |
| 12. | Die Idee der Rimannschen Fläche (Идея римановой поверхности), Leipzig, 1913. 2-е издание — Лейпциг, 1923; 3-е переработанное издание — Лейпциг, 1955; издание на английском языке — |
| 13. | Felix Klein Stellung in der mathematischen Gegenwart (Место Феликса Клейна в математической современности). Die Naturwissenschaften, 18, 1930, |
| 14. | Reine Infinitesimalgeotnetrie (Чистая инфинитезимальная геометрия). Mathematische Zeitschrift, 2, 1916, |
| 15. | Zur Infinitesimalgeometrie: Einordnung der projectiven und konformen Auffassung (К инфинитезимальной геометрии: введение проективной и конформной точек зрения). Göttinger Nachrichten, 1921, Перепечатано в «Избранном» (Selecta) Г. Вейля, |
| 16. | Was ist Materie? (Что такое материя?). Berlin, 1934. назад к тексту |
| 17. | Mathematische Analyse des Raumproblems (Математический анализ проблемы пространства). Berlin, 1923. назад к тексту |
| 18. | Симметрия. М., Наука, 1967. В английском оригинале книга Symmetry вышла в свет в 1952 г. в Принстоне (США); издание на немецком языке — Базель (Швейцария), 1955. назад к тексту |
| 19. | a) Ausbreitung elektrornagnetischer Wellen über einem ebenen Leiter (Распространение электромагнитных волн по плоскому проводнику). Annalen der Physik, 60, 1919, Статья а) перепечатана в «Избранном» Г. Вейля, |
| 20. | a) Gravitation und Elektrizität (Гравитация и электричество). Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin, 1918, Статья а) перепечатана в «Избранном» Г. Вейля, |
| 21. | Zur Infinitesimalgeometrie: p-dimensionale Flächen im |
| 22. | Die Einzigartigkeit der Pythagoreischen Massbestimmung (Единственность пифагорова мероопределения). Mathematische Zeitschrift, 12, 1922, |
| 23. | a) Sur une application de la théorie de nombres à la méchanique statistique et la théorie des perturbation (Об одном применении теории чисел к статистической механике и к теории возмущений). L'Enseignement mathématique, 16, 1914, |
| 24. | Análisis situs combinatorio (Комбинаторная топология). Revista Matematica Hispano-Americana, 5, 1923, 43 стр.; 6, 1924, К области топологии относится и самая последняя из опубликованных Г. Вейлем статей: Über die kombinatorische und kontinuumsmässige Definition der Überschneidungszahl zweier geschlossener Kurven auf einer Fläche (О комбинаторном и континуальном определении числа пересечений двух замкнутых кривых на поверхности). Zeitschrift für angewandte Mathematik und Physik, 4, 1953, |
| 25. | Introductión al análisis combinatorio (Введение в комбинаторный анализ). Revista Matematica Hispano-Americana, 5, 1923, Английский перевод — George Washington University Logistics Research Project, 1951. назад к тексту |
| 26. | Philosophie der Mathematik und Naturwissenschaft (Философия математики и естествознания). München, 1926. 2-е переработанное и дополненное издание — Мюнхен, 1950; издания на английском языке — Принстон (США), 1949, и Принстон, 1950. Отрывки из этой книги включены в сборник «Прикладная комбинаторная математика» (ред. Э. Ф. Беккенбах). М., Мир, 1968 (Applied Combinatorial Mathematics, edited by E. F. Beckenbach, |
| 27. | Über die Starrheit der Eiflächen und konvexer Polyeder (О жёсткости овалоидов и выпуклых многогранников). Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin, 1917, |
| 28. | Bemerkung über Hardy–Littlewoodschen Untersuchungen zum Waringschen Problem (Замечание об исследованиях Харди и Литтльвуда, посвящённых проблеме Варинга). Göttinger Nachrichten, 1921, |
| 29. | Elementary note on prime number problems of Vinogradoff's type (Элементарная заметка о связанных с простыми числами проблемах Виноградовского типа). Совм. с Р. Джемсом (R. D. James); American Journal of Mathematics, 64, 1942, |
| 30. | Das Kontinuum (Континуум). Leipzig, 1918. 2-е издание — Берлин, 1932. назад к тексту |
| 31. | Die Stufen des Unendlichen (Ступени бесконечности). Jena, 1931. назад к тексту |
| 32. | The open world (Открытый мир), London, 1932. 45 назад к тексту |
| 33. | Mind and Nature (Разум и природа). Philadelphia — London, 1934. назад к тексту |
| 34. | О полноте примитивных представлений компактной непрерывной группы. Совместно с Ф. Петером (F. Peter); Успехи математических наук [старая серия], вып. 2, 1936, В немецком оригинале статья вышла в свет в 1907 г. в журнале Mathematische Annalen, 97, |
| 35. | Theorie der Darstellung kontinuierlicher halbeinfacher Gruppen durch lineare Transformationen (Теория представлений непрерывных полупростых групп при помощи линейных преобразований). Mathematische Zeitschrift, 23, 1925, Перепечатано в «Избранном» Г. Вейля, |
| 36. | Electron und Gravitation (Электрон и гравитация) в Zeitschrift für Physik, 56, 1929, |
| 37. | а) On a problem in the theory of groups arising in the foundations of infinitesimal geometry (Об одной проблеме теории групп, возникающей в основаниях дифференциальной геометрии). Совместно с Г. Робертсоном (H. P. Robertson); Bulletin of the American Mathematical Society, 35, 1929, |
| 38. | а) The spherical symmetry of atoms (Сферическая симметрия атомов). The Rice Institute Pamphlet, 16, 1929, |
| 39. | Topologie und abstrakte Algebra als zwei Wege mathematischen Verständnisses (Топология и абстрактная алгебра как два пути математического мышления). Unterrichtsblätter für Mathematik und Naturwissenschaft, 38, 1932, |
| 40. | Eine für die Valenztheorie geeignete Basis der binären Vektorinvananten (Базис бинарных векторных инвариантов, приспособленный для теории валентности). Совместно с Э. Теллером (E. Teller) и Ю. Б. Румером; Göttinger Nachrichten, 1932, |
| 41. | Spinors in n dimensions (Спиноры в Перепечатано в «Избранном» Г. Вейля, |
| 42. | а) Harmonics on homogenous manifolds (Гармонические функции на однородных многообразиях). Annals of Mathematics, 35, 1934, Статья б) перепечатана в «Избранном» Г. Вейля, |
| 43. | Elementare Theorie der konvexen Polyeder (Элементарная теория выпуклого многогранника). Commentarii mathematici Helvetici, 7, 1936, Английский перевод — сборник «Исследования по теории игр I» (ред. Г. У. Кун и А. У. Таккер) (Contributions to the theory of games I, edited by H. W. Kuhn and A. W. Tucker), Принстон, 1950, |
| 44. | Elementary proof of a minmax theorem, due to |
| 45. | Классические группы, их инварианты и представления. М., В английском оригинале книга вышла в свет в 1939 г. в Принстоне (США); |
| 46. | Meromorphic functions and analytic curves (Мероморфные функции и аналитические кривые). Princeton, 1943. 46 назад к тексту |
| 47. | Fundamental domains for lattice groups in division algebras (Фундаментальные области для дискретных групп в алгебрах с делением). Festschrift zum 60. Geburtstag von Prof. Dr. A. Speiser (Юбилейный том к Обе части статьи перепечатаны в «Избранном» Г. Вейля, |
| 48. | Elementary algebraic treatment of the quantum mechanical symmetry problem (Элементарная алгебраическая трактовка квантово-механической проблемы симметрии). Canadian Journal of Mathematics, 1, 1949, Перепечатано в «Избранном» Г. Вейля, |
| 49. | A Half-century of Mathematics (Полвека математики). American Mathematical Monthly, 58, 1951, |
| 1. | Исходным пунктом всей современной дифференциальной геометрии «в малом» явилась замечательная речь Б. Римана «О гипотезах, лежащих в основании геометрии», произнесённая ещё в 1854 г., но по достоинству оценённая лишь после того, как Г. Вейль издал её со своими глубокими комментариями [1], раскрывающими на современном языке смысл конструкций Римана. Началом «геометрии в целом» как самостоятельного направления математической науки явилась классическая статья Г. Вейля [2]. Одним из лучших изложений алгебраической теории чисел является глубокая и блестящая по форме книга Г. Вейля [3]; в основе весьма многих построений аналитической теории чисел лежит старая статья Г. Вейля [4], также часто относимая сегодня к «математической классике». Может быть, лучшим и по сей день введением в математические методы теории относительности является замечательная книга Г. Вейля [5], о которой мы ещё подробнее скажем в дальнейшем; классическим сочинением, посвящённым построению математического аппарата квантовой механики, является монография Г. Вейля [6], впервые раскрывшая всё значение для современной физики идеи симметрии. (Цифры в квадратных скобках отсылают читателя к списку литературы на |
| 2. | Доступное для студентов-математиков изложение идей Г. Вейля и их последующего развития содержит не так давно переведённая на русский язык книга американского математика Дж. Спрингера «Введение в теорию римановых поверхностей». М., |
| 3. | См. Ф. Клейн. Сравнительное обозрение новейших геометрических: исследований («Эрлангенская программа»). Сб. Об основаниях геометрии. М., Гостехиздат, 1956, |
| 4. | Первая часть этих замечательных лекций переведена и на русский язык: Ф. Клейн. Лекции о развитии математики в XIX столетии, ч. I. |
| 5. | Ф. Клейн весьма высоко ценил Г. Вейля как выдающегося учёного, однако занятия последнего философией математики и основаниями математики (об этом мы ещё скажем ниже) оставались Клейну совершенно чужды: так, он до самой смерти не соглашался признать, что в теории вещественного числа остаются ещё нерешённые вопросы, достойные внимания математика. назад к тексту |
| 6. | Н. Weyl. Felix Klein Stelling in der mathematischen Gegenwart. Die Naturwissenschaften, 18, 1930, S. 5. (Перевод автора.) назад к тексту |
| 7. | H. Weyl. Felix Klein Stelling in der mathematischen Gegenwart. Die Naturwissenschaften, 18, 1930, S. 11. (Перевод автора.) назад к тексту |
| 8. | См. А. Эйнштейн. Основы общей теории относительности. Собрание научных трудов, т. I. M., Наука, 1965, На замечательную речь Римана внимание Эйнштейна обратил цюрихский математик М. Гроссман (M. Grossmann), которого Эйнштейн высоко ценил; однако трудно предположить, что Эйнштейн не обсуждал вопросы римановой геометрии и с таким специалистом в этой области, как его коллега Г. Вейль. назад к тексту |
| 9. | Напротив, в зарубежной методике математики в последнее время всё настойчивее проводится идея о необходимости полной перестройки школьного курса геометрии в направлении приближения его к современной концепции «векторного пространства», другими словами, — к аксиоматической схеме Г. Вейля. Эти идеи лежали в основе доклада на недавнем Международном конгрессе математиков в Москве одного из лидеров современного движения за модернизацию школьного курса математики, бельгийского алгебраиста Жоржа Папи́ — единственного большого доклада, заказанного оргкомитетом конгресса, который был прочитан на секции, посвящённой вопросам преподавания математики (см. Ж. Папи́. Геометрия в современном преподавании математики. Журн. Математика в школе, 1967, № 1, |
| 10. | Рассчитанное на учителя средней школы изложение аксиоматики Вейля можно найти, например, в кн. IV «Энциклопедии элементарной математики» (М., Физматгиз, 1963, |
| 11. | Точнее — псевдоэвклидова (см. выше). назад к тексту |
| 12. | См. сб. «Об основаниях геометрии». М., Гостехиздат, 1956, |
| 13. | Следует напомнить, что результатом продумывания философом Кантом физических и космогонических проблем (в книге «Что такое материя?» [16] космологическим проблемам уделено весьма много места) явилась интересная космогоническая гипотеза (так называемая гипотеза Канта–Лапласа), сыгравшая в истории астрономии очень важную роль. назад к тексту |
| 14. | Мы не останавливаемся здесь более подробно на интереснейшей теме — Г. Вейль и дискретная математика, отсылая читателя к сборнику «Прикладная комбинаторная математика» (ред. Э. Ф. Беккенбах), М., Мир, 1968, содержащему отрывки из книги [26] Вейля. (Интересно, что и «Ars combinatoria» Вейля, подобно его книге [5], открывается стихотворным эпиграфом — на этот раз из «Кавалера роз» Гуго фон Гофмансталя.) назад к тексту |
| 15. | Обзор современного состояния исследований по проблеме Вейля см. в книге Г. Бузман. Выпуклые поверхности. М., Наука, 1964, в которой, в частности, обстоятельно изложены достижения в этой области ленинградской геометрической школы. назад к тексту |
| 16. | И. М. Виноградов доказал, что каждое нечётное число, большее некоторого (очень большого!) |
| 17. | Относительно современных концепций обоснования математики см., например, книгу А. Гейтинг. Интуиционизм. М., Мир, 1965, автор которой является видным сторонником точки зрения Г. Вейля. (На русском языке имеется также сборник [11] статей самого Вейля, хорошо отражающих его основные установки). назад к тексту |
| 18. | Жена Г. Вейля Елена (Хела) Вейль — большой знаток испанской поэзии и философии, — перевела на немецкий язык ряд произведений Ортега-и-Гассета. назад к тексту |
| 19. | Вопрос 4: Свойства симметрии. Исследуйте свойства уравнения Дирака по отношению к вращению: а) когда вращается доска, на которой уравнение написано; б) когда вращается физик, исследующий это уравнение. (См. сб. «Физики шутят». М., Мир, 1966, стр.56). назад к тексту |
| 20. | См., например, Э. Бауэр. Введение в теорию групп и её приложения к квантовой механике. |
| 21. | См. превосходную научно-популярную книгу: Кеннет Форд. Мир элементарных частиц. М., Мир, 1965, уделяющую весьма много места соображениям симметрии (без которых сегодня немыслимо говорить об элементарных частицах даже в книге для начинающих!). назад к тексту |
| 22. | См. Л. Д. Ландау. О законах сохранения при слабых взаимодействиях. Журнал экспериментальной и теоретической физики, т. 32, вып. 2, 1957, |
| 23. | См., например, хорошую научно-популярную статью известного американского физика-теоретика Ф. Дайсона «Математика и физика». Успехи физических наук, т. 85, вып. 2, 1965, |
| 24. | См., например, Я. Б. Зельдович, Л. Б. Окунь и С. Б. Пикельнер, Кварки: астрофизический и физико-химический аспекты. Успехи физических наук, т. 87, вып. 1, 1965, |
| 25. | См. В. Паули. Общие принципы волновой механики. |
| 26. | См. §14 статьи Б. Л. ван дер Варден. Принцип запрета и спин, в посвящённом памяти В. Паули сборнике «Теоретическая физика |
| 27. | Этот цикл работ начался статьёй: И. М. Гельфанд и Д. А. Райков. Неприводимые унитарные представления локально-бикомпактных групп. Математический сборник, т. 13 (55), 1943, |
| 28. | Отметим всё же статью общего содержания «Топология и абстрактная алгебра как два пути математического мышления» [39], предвосхитившую некоторые идеи, характерные для более позднего времени, а также статью «Базис бинарных векторных инвариантов, пригодный для теории валентности» [40], в которой типичные для Вейля математические построения приспосабливаются для использования их в химической теории валентности. назад к тексту |
| 29. | Важность этой тематики была подчёркнута присуждением Ю. Вигнеру в 1963 г. — через восемь лет после смерти Г. Вейля — Нобелевской премии по физике. назад к тексту |
| 30. | Сборник этот положил начало целой серии подобных же сборников, выпущенных в разные годы издательством Принстонского университета. На русский язык переведён один из более поздних сборников. — «Линейные неравенства» (ред. Г. У. Кун и А. У. Таккер). М., |
| 31. | Известный финский математик Ларс В. Альфорс, специалист по теории функций комплексного переменного. назад к тексту |
| 32. | H. Weyl. Meromorphic functions and analytic curves, Princeton, 1943, p. 3. (Перевод автора.) назад к тексту |
| 33. | В смысле «правильности», «соразмерности». |
| 34. | Самые известные из международных математических премий, выдаваемые молодым учёным раз в четыре года во время Международных математических конгрессов. назад к тексту |
| 35. | См., например, П. Бейсвангер (Peter Beiswanger). Эволюция взглядов Германа Вейля на математику (Die Phasen in Hermann Weyl's Beurteilung der Mathematik), |
| 36. | См., например, Р. Леупольд (Rudolf Leupold), Исследования Германа Вейля в области оснований математики (Die Grundlagenforschung bei Hermann Weyl). Эта диссертация на степень доктора философии защищалась в Майнцском университете имени И. Гутенберга в 1960 г. назад к тексту |
| 37. | См., например, статью Н. Бурбаки. Архитектура математики. Сб. Математическое просвещение, вып. 5. М., Физматгиз, 1960, |
|
Яглом Исаак Моисеевич ГЕРМАН ВЕЙЛЬ Редактор В. Ю. Иваницкий Худож. редактор Е. Е. Соколов Техн. редактор Е. М. Лопухова Корректор В. И. Казакова Художник П. Цепелинский А 12570. Цена 9 коп. |